- Tổng quan
- Nội dung
- Tiêu chuẩn liên quan
- Lược đồ
- Tải về
Tiêu chuẩn TCVN 8006-7:2013 Thiết lập ước lượng, khoảng tin cậy đối với trung vị trong thống kê
| Số hiệu: | TCVN 8006-7:2013 | Loại văn bản: | Tiêu chuẩn Việt Nam |
| Cơ quan ban hành: | Bộ Khoa học và Công nghệ | Lĩnh vực: | Khoa học-Công nghệ |
|
Ngày ban hành:
Ngày ban hành là ngày, tháng, năm văn bản được thông qua hoặc ký ban hành.
|
2013 |
Hiệu lực:
|
Đã biết
|
| Người ký: | Đang cập nhật |
Tình trạng hiệu lực:
Cho biết trạng thái hiệu lực của văn bản đang tra cứu: Chưa áp dụng, Còn hiệu lực, Hết hiệu lực, Hết hiệu lực 1 phần; Đã sửa đổi, Đính chính hay Không còn phù hợp,...
|
Đã biết
|
TÓM TẮT TIÊU CHUẨN VIỆT NAM TCVN 8006-7:2013
Nội dung tóm tắt đang được cập nhật, Quý khách vui lòng quay lại sau!
Tải tiêu chuẩn Việt Nam TCVN 8006-7:2013
TIÊU CHUẨN QUỐC GIA
TCVN 8006-7:2013
ISO 16269-7:2001
GIẢI THÍCH CÁC DỮ LIỆU THỐNG KÊ - PHẦN 7: TRUNG VỊ - ƯỚC LƯỢNG VÀ KHOẢNG TIN CẬY
Statistical interpretation of data - Part 7: Median - Estimation and confidence intervals
Lời nói đầu
TCVN 8006-7:2013 hoàn toàn tương đương với ISO 16269-7:2001;
TCVN 8006-7:2013 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 8006, chấp nhận bộ tiêu chuẩn ISO 16269, gồm các tiêu chuẩn dưới đây có tên chung “Giải thích các dữ liệu thống kê”:
- TCVN 8006-4:2013 (ISO 16269-4:2010), Phần 4: Phát hiện và xử lý các giá trị bất thường
- TCVN 8006-6:2009 (ISO 16269-6:2005), Phần 6: Xác định khoảng dung sai thống kê
- TCVN 8006-7:2013 (ISO 16269-7:2001), Phần 7: Trung vị - Ước lượng và khoảng tin cậy
Bộ tiêu chuẩn ISO 16269 còn có tiêu chuẩn sau:
- ISO 16269-8, Statistical interpretation of data - Part 8: Determination of prediction intervals
GIẢI THÍCH CÁC DỮ LIỆU THỐNG KÊ - PHẦN 7: TRUNG VỊ - ƯỚC LƯỢNG VÀ KHOẢNG TIN CẬY
Statistical interpretation of data - Part 7: Median - Estimation and confidence intervals
1. Phạm vi áp dụng
Tiêu chuẩn này quy định các qui trình thiết lập ước lượng điểm và khoảng tin cậy đối với trung vị của phân bố xác suất liên tục bất kỳ của một tổng thể dựa trên cỡ mẫu ngẫu nhiên lấy từ tổng thể đó. Các quy trình này không phụ thuộc phân bố, nghĩa là chúng không đòi hỏi hiểu biết về phân bố của tổng thể đó thuộc về họ phân bố nào. Các quy trình tương tự có thể áp dụng để ước lượng tứ phân vị và phân vị.
CHÚ THÍCH: Trung vị là tứ phân vị thứ hai và phân vị thứ năm mươi. Các quy trình tương tự dùng cho tứ phân vị hay phân vị khác không được mô tả trong tiêu chuẩn này.
2. Tài liệu viện dẫn
Các tài liệu viện dẫn trong tiêu chuẩn này rất cần thiết cho việc áp dụng tiêu chuẩn. Đối với các tài liệu có ghi năm công bố thì áp dụng bản được nêu. Đối với các tài liệu không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi.
TCVN 8244-1 (ISO 3534-1), Thống kê - Từ vựng và ký hiệu - Phần 1: Thuật ngữ chung về xác suất và thống kê
ISO 2602, Statistical interpretation of test results - Estimation of the mean - Confidence interval (Giải thích thống kê các kết quả thử - Ước lượng trung bình - Khoảng tin cậy)
3. Thuật ngữ, định nghĩa và ký hiệu
3.1. Thuật ngữ và định nghĩa
Tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa trong TCVN 8244-1 (ISO 3534-1) và ISO 2602 và các thuật ngữ, định nghĩa dưới đây.
3.1.1. Thống kê thứ tự thứ k của mẫu (kth order statistic of a sample)
Giá trị của phần tử thứ k trong mẫu khi các phần tử được sắp xếp theo thứ tự giá trị không giảm của chúng.
CHÚ THÍCH: Đối với mẫu gồm n phần tử sắp xếp theo thứ tự không giảm, thống kê thứ tự thứ k là x[k] trong đó
x[1] ≤ x[2] ≤ … ≤ x[n]
3.1.2. Trung vị của phân bố xác suất liên tục (median of a continuous probability distribution)
Giá trị sao cho tỷ lệ của phân bố nằm ở một trong hai phía của nó đều bằng một nửa.
CHÚ THÍCH: Trong tiêu chuẩn này, trung vị của phân bố xác suất liên tục được gọi là trung vị tổng thể và ký hiệu là M.
3.2. Ký hiệu
Tiêu chuẩn này sử dụng các ký hiệu dưới đây.
| a | giới hạn dưới của các giá trị của biến trong tổng thể |
| b | giới hạn trên của các giá trị của biến trong tổng thể |
| C | mức tin cậy |
| c | hằng số sử dụng cho việc xác định giá trị của k trong công thức (1) |
| k | số của thống kê thứ tự sử dụng cho giới hạn tin cậy dưới |
| M | trung vị tổng thể |
| n | cỡ mẫu |
| T1 | giới hạn tin cậy dưới rút ra từ mẫu |
| T2 | giới hạn tin cậy trên rút ra từ mẫu |
| u | tỷ số biểu thị biến của phân bố chuẩn chuẩn hóa |
| x[i] | phần tử nhỏ nhất thứ i trong mẫu khi các phần tử được sắp xếp theo thứ tự giá trị không tăng |
|
| trung vị mẫu |
| y | giá trị trung gian được tính để xác định k sử dụng công thức (1) |
4. Khả năng áp dụng
Phương pháp mô tả trong tiêu chuẩn này có hiệu lực đối với phân bố liên tục bất kỳ với điều kiện là mẫu được lấy ngẫu nhiên.
CHÚ THÍCH: Nếu phân bố của tổng thể có thể giả định là xấp xỉ phân bổ chuẩn thì trung vị tổng thể xấp xỉ bằng trung bình tổng thể và giới hạn tin cậy có thể được tính theo ISO 2602.
5. Ước lượng điểm
Ước lượng điểm của trung vị tổng thể được cho bởi trung vị mẫu, ![]() . Trung vị mẫu thu được bằng cách đánh số các phần tử mẫu theo thứ tự giá trị không giảm và lấy giá trị của
. Trung vị mẫu thu được bằng cách đánh số các phần tử mẫu theo thứ tự giá trị không giảm và lấy giá trị của
- thống kê thứ tự thứ [(n + 1)/2], nếu n lẻ, hoặc
- trung bình cộng của các thống kê thứ tự thứ (n/2) và [(n/2 + 1)], nếu n chẵn.
CHÚ THÍCH: Hàm ước lượng này nói chung là chệch đối với phân bố không đối xứng, tuy nhiên, không tồn tại hàm ước lượng không chệch đối với phân bố bất kỳ.
6. Khoảng tin cậy
6.1. Quy định chung
Khoảng tin cậy hai phía đối với trung vị tổng thể là khoảng đóng có dạng [T1, T2], trong đó T1 < T2; T1 và T2 tương ứng được gọi là giới hạn tin cậy dưới và trên.
Nếu a và b tương ứng là giới hạn dưới và trên của biến trong tổng thể thì khoảng tin cậy một phía sẽ có dạng [T1, b] hoặc dạng [a, T2].
CHÚ THÍCH: Ví mục đích thực tiễn, a thường được lấy bằng 0 đối với các biến không thể âm, và b thường được lấy là vô hạn đối với các biến không có giới hạn trên tự nhiên.
Ý nghĩa thực tế của khoảng tin cậy là nhà thực nghiệm công bố rằng M chưa biết nằm trong khoảng đó, đồng thời thừa nhận rằng khẳng định này có thể sai với xác suất danh nghĩa nhỏ. Xác suất để khoảng tính theo cách thức bao trùm trung vị tổng thể được gọi là mức tin cậy.
6.2. Phương pháp truyền thống
Phương pháp truyền thống được mô tả trong Phụ lục A. Nó liên quan đến việc giải một cặp bất đẳng thức. Cách khác để giải các bất đẳng thức này được nêu dưới đây đối với một loạt các mức tin cậy.
6.3. Mẫu nhỏ (5 ≤ n ≤ 100)
Các giá trị k thỏa mãn công thức trong Phụ lục A đối với tám mức tin cậy được sử dụng phổ biến nhất cho các cỡ mẫu khác nhau từ 5 đến 100 đơn vị mẫu được cho trong Bảng 1 đối với trường hợp một phía và Bảng 2 đối với trường hợp hai phía. Giá trị của k được cho để giới hạn tin cậy dưới là
T1 = x[k]
và giới hạn tin cậy trên là
T2 = x[n-k+1]
trong đó x[1], x[2], …., x[n] là các giá trị quan trắc trong mẫu được sắp thứ tự.
Đối với các giá trị n nhỏ, có thể xảy ra việc giới hạn tin cậy dựa trên thống kê thứ tự không thấy có ở những mức tin cậy nhất định.
Ví dụ việc tính toán giới hạn tin cậy đối với các mẫu nhỏ được cho trong B.1 và thể hiện trên Mẫu A của Phụ lục B.
6.4. Mẫu lớn (n > 100)
Đối với các cỡ mẫu vượt quá 100 đơn vị mẫu, giá trị gần đúng của k đối với mức tin cậy (1 - a) có thể được xác định là phần nguyên của giá trị thu được từ công thức sau:
![]() (1)
(1)
trong đó
u là tỷ số biểu thị biến của phân bố chuẩn chuẩn hóa; giá trị của u được cho trong Bảng 3 đối với khoảng tin cậy một phía và trong Bảng 4 đối với khoảng hai phía;
c được cho trong Bảng 3 đối với khoảng tin cậy một phía và trong Bảng 4 đối với khoảng hai phía.
Giá trị của k thu được bằng công thức thực nghiệm (1) thống nhất hoàn toàn với giá trị đúng được cho trong Bảng 1 và 2. Với điều kiện tất cả 8 chữ số thập phân của u được duy trì, phép xấp xỉ này đặc biệt chính xác và cho giá trị k đúng đối với cả tám mức tin cậy ở tất cả các cỡ mẫu từ 5 đến trên 280 000, với cả khoảng tin cậy một phía và hai phía.
Ví dụ việc tính toán giới hạn tin cậy đối với các mẫu lớn được cho trong B.2 và thể hiện trên Mẫu B của Phụ lục B.
CHÚ THÍCH: Để dễ dàng sử dụng, các giá trị của c trong Bảng 3 và Bảng 4 được cho theo số lượng chữ số thập phân tối thiểu cần thiết để đảm bảo độ chính xác cao nhất có thể của công thức (1).
Bảng 1 - Giá trị chính xác của k đối với các cỡ mẫu khác nhau từ 5 đến 100: trường hợp một phía
| Cỡ mẫu n | k | Cỡ mẫu n | k | ||||||||||||||
| Mức tin cậy | Mức tin cậy | ||||||||||||||||
| 80 | 90 | 95 | 98 | 99 | 99,5 | 99,8 | 99,9 | 80 | 90 | 95 | 98 | 99 | 99,5 | 99,8 | 99,9 | ||
| 5 | 2 | 1 | 1 | a | a | a | a | a | 55 | 24 | 23 | 21 | 20 | 19 | 18 | 17 | 16 |
| 6 | 2 | 1 | 1 | 1 | a | a | a | a | 56 | 25 | 23 | 22 | 20 | 19 | 18 | 17 | 17 |
| 7 | 2 | 2 | 1 | 1 | 1 | a | a | a | 57 | 25 | 24 | 22 | 21 | 20 | 19 | 18 | 17 |
| 8 | 3 | 2 | 2 | 1 | 1 | 1 | a | a | 58 | 26 | 24 | 23 | 21 | 20 | 19 | 18 | 17 |
| 9 | 3 | 3 | 2 | 2 | 1 | 1 | 1 | a | 59 | 26 | 25 | 23 | 22 | 21 | 20 | 19 | 18 |
| 10 | 4 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 60 | 27 | 25 | 24 | 22 | 21 | 20 | 19 | 18 |
| 11 | 4 | 3 | 3 | 2 | 2 | 1 | 1 | 1 | 61 | 27 | 25 | 24 | 23 | 21 | 21 | 19 | 19 |
| 12 | 5 | 4 | 3 | 3 | 2 | 2 | 1 | 1 | 62 | 28 | 26 | 25 | 23 | 22 | 21 | 20 | 19 |
| 13 | 5 | 4 | 4 | 3 | 2 | 2 | 2 | 1 | 63 | 28 | 26 | 25 | 23 | 22 | 21 | 20 | 19 |
| 14 | 5 | 5 | 4 | 3 | 3 | 2 | 2 | 2 | 64 | 29 | 27 | 25 | 24 | 23 | 22 | 21 | 20 |
| 15 | 6 | 5 | 4 | 4 | 3 | 3 | 2 | 2 | 65 | 29 | 27 | 26 | 24 | 23 | 22 | 21 | 20 |
| 16 | 6 | 5 | 5 | 4 | 3 | 3 | 2 | 2 | 66 | 30 | 28 | 26 | 25 | 24 | 23 | 21 | 21 |
| 17 | 7 | 6 | 5 | 4 | 4 | 3 | 3 | 2 | 67 | 30 | 28 | 27 | 25 | 24 | 23 | 22 | 21 |
| 18 | 7 | 6 | 6 | 5 | 4 | 4 | 3 | 3 | 68 | 31 | 29 | 27 | 26 | 24 | 23 | 22 | 21 |
| 19 | 8 | 7 | 6 | 5 | 5 | 4 | 3 | 3 | 69 | 31 | 29 | 28 | 26 | 25 | 24 | 23 | 22 |
| 20 | 8 | 7 | 6 | 5 | 5 | 4 | 4 | 3 | 70 | 31 | 30 | 28 | 26 | 25 | 24 | 23 | 22 |
| 21 | 9 | 8 | 7 | 6 | 5 | 5 | 4 | 4 | 71 | 32 | 30 | 29 | 27 | 26 | 25 | 23 | 23 |
| 22 | 9 | 8 | 7 | 6 | 6 | 5 | 4 | 4 | 72 | 32 | 31 | 29 | 27 | 26 | 25 | 24 | 23 |
| 23 | 9 | 8 | 8 | 7 | 6 | 5 | 5 | 4 | 73 | 33 | 31 | 29 | 28 | 27 | 26 | 24 | 23 |
| 24 | 10 | 9 | 8 | 7 | 6 | 6 | 5 | 5 | 74 | 33 | 31 | 30 | 28 | 27 | 26 | 25 | 24 |
| 25 | 10 | 9 | 8 | 7 | 7 | 6 | 5 | 5 | 75 | 34 | 32 | 30 | 29 | 27 | 26 | 25 | 24 |
| 26 | 11 | 10 | 9 | 8 | 7 | 7 | 6 | 5 | 76 | 34 | 32 | 31 | 29 | 28 | 27 | 26 | 25 |
| 27 | 11 | 10 | 9 | 8 | 8 | 7 | 6 | 6 | 77 | 35 | 33 | 31 | 30 | 28 | 27 | 26 | 25 |
| 28 | 12 | 11 | 10 | 9 | 8 | 7 | 7 | 6 | 78 | 35 | 33 | 32 | 30 | 29 | 28 | 26 | 25 |
| 29 | 12 | 11 | 10 | 9 | 8 | 8 | 7 | 6 | 79 | 36 | 34 | 32 | 30 | 29 | 28 | 27 | 26 |
| 30 | 13 | 11 | 11 | 9 | 9 | 8 | 7 | 7 | 80 | 36 | 34 | 33 | 31 | 30 | 29 | 27 | 26 |
| 31 | 13 | 12 | 11 | 10 | 9 | 8 | 8 | 7 | 81 | 37 | 35 | 33 | 31 | 30 | 29 | 28 | 27 |
| 32 | 14 | 12 | 11 | 10 | 9 | 9 | 8 | 7 | 82 | 37 | 35 | 34 | 32 | 31 | 29 | 28 | 27 |
| 33 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 8 | 83 | 38 | 36 | 34 | 32 | 31 | 30 | 28 | 28 |
| 34 | 15 | 13 | 12 | 11 | 10 | 10 | 9 | 8 | 84 | 38 | 36 | 34 | 33 | 31 | 30 | 29 | 28 |
| 35 | 15 | 14 | 13 | 11 | 11 | 10 | 9 | 9 | 85 | 39 | 37 | 35 | 33 | 32 | 31 | 29 | 28 |
| 36 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 9 | 86 | 39 | 37 | 35 | 34 | 32 | 31 | 30 | 29 |
| 37 | 16 | 15 | 14 | 12 | 11 | 11 | 10 | 9 | 87 | 40 | 38 | 36 | 34 | 33 | 32 | 30 | 29 |
| 38 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 88 | 40 | 38 | 36 | 34 | 33 | 32 | 31 | 30 |
| 39 | 17 | 16 | 14 | 13 | 12 | 12 | 11 | 10 | 89 | 41 | 38 | 37 | 35 | 34 | 32 | 31 | 30 |
| 40 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 90 | 41 | 39 | 37 | 35 | 34 | 33 | 31 | 30 |
| 41 | 18 | 16 | 15 | 14 | 13 | 12 | 11 | 11 | 91 | 41 | 39 | 38 | 36 | 34 | 33 | 32 | 31 |
| 42 | 18 | 17 | 16 | 14 | 14 | 13 | 12 | 11 | 92 | 42 | 40 | 38 | 36 | 35 | 34 | 32 | 31 |
| 43 | 19 | 17 | 16 | 15 | 14 | 13 | 12 | 12 | 93 | 42 | 40 | 39 | 37 | 35 | 34 | 33 | 32 |
| 44 | 19 | 18 | 17 | 15 | 14 | 14 | 13 | 12 | 94 | 43 | 41 | 39 | 37 | 36 | 35 | 33 | 32 |
| 45 | 20 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 95 | 43 | 41 | 39 | 38 | 36 | 35 | 34 | 33 |
| 46 | 20 | 19 | 17 | 16 | 15 | 14 | 13 | 13 | 96 | 44 | 42 | 40 | 38 | 37 | 35 | 34 | 33 |
| 47 | 21 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 97 | 44 | 42 | 40 | 38 | 37 | 36 | 34 | 33 |
| 48 | 21 | 20 | 18 | 17 | 16 | 15 | 14 | 13 | 98 | 45 | 43 | 41 | 39 | 38 | 36 | 35 | 34 |
| 49 | 22 | 20 | 19 | 17 | 16 | 16 | 15 | 14 | 99 | 45 | 43 | 41 | 39 | 38 | 37 | 35 | 34 |
| 50 | 22 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 100 | 46 | 44 | 42 | 40 | 38 | 37 | 36 | 35 |
| 51 | 22 | 21 | 20 | 18 | 17 | 16 | 15 | 15 |
|
|
|
|
|
|
|
|
|
| 52 | 23 | 21 | 20 | 19 | 18 | 17 | 16 | 15 |
|
|
|
|
|
|
|
|
|
| 53 | 23 | 22 | 21 | 19 | 18 | 17 | 16 | 15 |
|
|
|
|
|
|
|
|
|
| 54 | 24 | 22 | 21 | 19 | 19 | 18 | 17 | 16 |
|
|
|
|
|
|
|
|
|
| a Không thể xác định được khoảng tin cậy và giới hạn tin cậy đối với cỡ mẫu này ở mức tin cậy này. | |||||||||||||||||
Bảng 2 - Giá trị chính xác của k đối với các cỡ mẫu khác nhau từ 5 đến 100: trường hợp hai phía
| Cỡ mẫu | k | Cỡ mẫu n | k | ||||||||||||||
| Mức tin cậy | Mức tin cậy | ||||||||||||||||
| 80 | 90 | 95 | 98 | 99 | 99,5 | 99,8 | 99,9 | 80 | 90 | 95 | 98 | 99 | 99,5 | 99,8 | 99,9 | ||
| 5 | 1 | 1 | a | a | a | a | a | a | 55 | 23 | 21 | 20 | 19 | 18 | 17 | 16 | 15 |
| 6 | 1 | 1 | 1 | a | a | a | a | a | 56 | 23 | 22 | 21 | 19 | 18 | 18 | 17 | 16 |
| 7 | 2 | 1 | 1 | 1 | a | a | a | a | 57 | 24 | 22 | 21 | 20 | 19 | 18 | 17 | 16 |
| 8 | 2 | 2 | 1 | 1 | 1 | a | a | a | 58 | 24 | 23 | 22 | 20 | 19 | 18 | 17 | 17 |
| 9 | 3 | 2 | 2 | 1 | 1 | 1 | a | a | 59 | 25 | 23 | 22 | 21 | 20 | 19 | 18 | 17 |
| 10 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | a | 60 | 25 | 24 | 22 | 21 | 20 | 19 | 18 | 17 |
| 11 | 3 | 3 | 2 | 2 | 1 | 1 | 1 | 1 | 61 | 25 | 24 | 23 | 21 | 21 | 20 | 19 | 18 |
| 12 | 4 | 3 | 3 | 2 | 2 | 1 | 1 | 1 | 62 | 26 | 25 | 23 | 22 | 21 | 20 | 19 | 18 |
| 13 | 4 | 4 | 3 | 2 | 2 | 2 | 1 | 1 | 63 | 26 | 25 | 24 | 22 | 21 | 20 | 19 | 19 |
| 14 | 5 | 4 | 3 | 3 | 2 | 2 | 2 | 1 | 64 | 27 | 25 | 24 | 23 | 22 | 21 | 20 | 19 |
| 15 | 5 | 4 | 4 | 3 | 3 | 2 | 2 | 2 | 65 | 27 | 26 | 25 | 23 | 22 | 21 | 20 | 19 |
| 16 | 5 | 5 | 4 | 3 | 3 | 3 | 2 | 2 | 66 | 28 | 26 | 25 | 24 | 23 | 22 | 21 | 20 |
| 17 | 6 | 5 | 5 | 4 | 3 | 3 | 2 | 2 | 67 | 28 | 27 | 26 | 24 | 23 | 22 | 21 | 20 |
| 18 | 6 | 6 | 5 | 4 | 4 | 3 | 3 | 2 | 68 | 29 | 27 | 26 | 24 | 23 | 23 | 21 | 21 |
| 19 | 7 | 6 | 5 | 5 | 4 | 4 | 3 | 3 | 69 | 29 | 28 | 26 | 25 | 24 | 23 | 22 | 21 |
| 20 | 7 | 6 | 6 | 5 | 4 | 4 | 3 | 3 | 70 | 30 | 28 | 27 | 25 | 24 | 23 | 22 | 21 |
| 21 | 8 | 7 | 6 | 5 | 5 | 4 | 4 | 3 | 71 | 30 | 29 | 27 | 26 | 25 | 24 | 23 | 22 |
| 22 | 8 | 7 | 6 | 6 | 5 | 5 | 4 | 4 | 72 | 31 | 29 | 28 | 26 | 25 | 24 | 23 | 22 |
| 23 | 8 | 8 | 7 | 6 | 5 | 5 | 4 | 4 | 73 | 31 | 29 | 28 | 27 | 26 | 25 | 23 | 23 |
| 24 | 9 | 8 | 7 | 6 | 6 | 5 | 5 | 4 | 74 | 31 | 30 | 29 | 27 | 26 | 25 | 24 | 23 |
| 25 | 9 | 8 | 8 | 7 | 6 | 6 | 5 | 5 | 75 | 32 | 30 | 29 | 27 | 26 | 25 | 24 | 23 |
| 26 | 10 | 9 | 8 | 7 | 7 | 6 | 5 | 5 | 76 | 32 | 31 | 29 | 28 | 27 | 26 | 25 | 24 |
| 27 | 10 | 9 | 8 | 8 | 7 | 6 | 6 | 5 | 77 | 33 | 31 | 30 | 28 | 27 | 26 | 25 | 24 |
| 28 | 11 | 10 | 9 | 8 | 7 | 7 | 6 | 6 | 78 | 33 | 32 | 30 | 29 | 28 | 27 | 25 | 25 |
| 29 | 11 | 10 | 9 | 8 | 8 | 7 | 6 | 6 | 79 | 34 | 32 | 31 | 29 | 28 | 27 | 26 | 25 |
| 30 | 11 | 11 | 10 | 9 | 8 | 7 | 7 | 6 | 80 | 34 | 33 | 31 | 30 | 29 | 28 | 26 | 25 |
| 31 | 12 | 11 | 10 | 9 | 8 | 8 | 7 | 7 | 81 | 35 | 33 | 32 | 30 | 29 | 28 | 27 | 26 |
| 32 | 12 | 11 | 10 | 9 | 9 | 8 | 7 | 7 | 82 | 35 | 34 | 32 | 31 | 29 | 28 | 27 | 26 |
| 33 | 13 | 12 | 11 | 10 | 9 | 9 | 8 | 7 | 83 | 36 | 34 | 33 | 31 | 30 | 29 | 28 | 27 |
| 34 | 13 | 12 | 11 | 10 | 10 | 9 | 8 | 8 | 84 | 36 | 34 | 33 | 31 | 30 | 29 | 28 | 27 |
| 35 | 14 | 13 | 12 | 11 | 10 | 9 | 9 | 8 | 85 | 37 | 35 | 33 | 32 | 31 | 30 | 28 | 27 |
| 36 | 14 | 13 | 12 | 11 | 10 | 10 | 9 | 8 | 86 | 37 | 35 | 34 | 32 | 31 | 30 | 29 | 28 |
| 37 | 15 | 14 | 13 | 11 | 11 | 10 | 9 | 9 | 87 | 38 | 36 | 34 | 33 | 32 | 30 | 29 | 28 |
| 38 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 9 | 88 | 38 | 36 | 35 | 33 | 32 | 31 | 30 | 29 |
| 39 | 16 | 14 | 13 | 12 | 12 | 11 | 10 | 9 | 89 | 38 | 37 | 35 | 34 | 32 | 31 | 30 | 29 |
| 40 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 10 | 90 | 39 | 37 | 36 | 34 | 33 | 32 | 30 | 30 |
| 41 | 16 | 15 | 14 | 13 | 12 | 12 | 11 | 10 | 91 | 39 | 38 | 36 | 34 | 33 | 32 | 31 | 30 |
| 42 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 11 | 92 | 40 | 38 | 37 | 35 | 34 | 33 | 31 | 30 |
| 43 | 17 | 16 | 15 | 14 | 13 | 12 | 12 | 11 | 93 | 40 | 39 | 37 | 35 | 34 | 33 | 32 | 31 |
| 44 | 18 | 17 | 16 | 14 | 14 | 13 | 12 | 11 | 94 | 41 | 39 | 38 | 36 | 35 | 33 | 32 | 31 |
| 45 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 12 | 95 | 41 | 39 | 38 | 36 | 35 | 34 | 33 | 32 |
| 46 | 19 | 17 | 16 | 15 | 14 | 14 | 13 | 12 | 96 | 42 | 40 | 38 | 37 | 35 | 34 | 33 | 32 |
| 47 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 97 | 42 | 40 | 39 | 37 | 36 | 35 | 33 | 32 |
| 48 | 20 | 18 | 17 | 16 | 15 | 14 | 13 | 13 | 98 | 43 | 41 | 39 | 38 | 36 | 35 | 34 | 33 |
| 49 | 20 | 19 | 18 | 16 | 16 | 15 | 14 | 13 | 99 | 43 | 41 | 40 | 38 | 37 | 36 | 34 | 33 |
| 50 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 14 | 100 | 44 | 42 | 40 | 38 | 37 | 36 | 35 | 34 |
| 51 | 21 | 20 | 19 | 17 | 16 | 16 | 15 | 14 |
|
|
|
|
|
|
|
|
|
| 52 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 |
|
|
|
|
|
|
|
|
|
| 53 | 22 | 21 | 19 | 18 | 17 | 16 | 15 | 15 |
|
|
|
|
|
|
|
|
|
| 54 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 |
|
|
|
|
|
|
|
|
|
| a Không thể xác định được khoảng tin cậy và giới hạn tin cậy đối với cỡ mẫu này ở mức tin cậy này. | |||||||||||||||||
| Bảng 3 - Giá trị của u và c đối với trường hợp một phía |
| Bảng 4 - Giá trị của u và c đối với trường hợp hai phía | ||||
| Mức tin cậy % | u | c |
| Mức tin cậy % | u | c |
| 80,0 | 0,841 621 22 | 0,75 |
| 80,0 | 1,281 551 56 | 0,903 |
| 90,0 | 1,281 551 56 | 0,903 |
| 90,0 | 1,644 853 64 | 1,087 |
| 95,0 | 1,644 853 64 | 1,087 |
| 95,0 | 1,959 964 00 | 1,274 |
| 98,0 | 2,053 748 92 | 1,3375 |
| 98,0 | 2,326 347 88 | 1,536 |
| 99,0 | 2,326 347 88 | 1,536 |
| 99,0 | 2,575 829 30 | 1,74 |
| 99,5 | 2,575 829 30 | 1,74 |
| 99,5 | 2,807 033 76 | 1,945 |
| 99,8 | 2,878 161 73 | 2,014 |
| 99,8 | 3,090 232 29 | 2,222 |
| 99,9 | 3,090 232 29 | 2,222 |
| 99,9 | 3,290 562 72 | 2,437 |
Phụ lục A
(tham khảo)
Phương pháp truyền thống xác định giới hạn tin cậy đối với trung vị
Giả định rằng mẫu cỡ n được lấy ngẫu nhiên từ một tổng thể liên tục. Trong các điều kiện này, xác suất để có chính xác k giá trị mẫu nhỏ hơn trung vị tổng thể được mô tả bằng phân bố nhị phân:
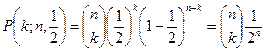
Đây cũng là xác suất để có chính xác k giá trị mẫu lớn hơn trung vị tổng thể.
Giới hạn dưới và giới hạn trên của khoảng tin cậy hai phía với mức tin cậy (1 - a) được cho bởi cặp thống kê thứ tự (x[k], x[n-k+1]), trong đó số nguyên k được xác định sao cho
![]() (A.1)
(A.1)
và
![]() ; (A.2)
; (A.2)
nghĩa là
![]() (A.3)
(A.3)
và
![]() (A.4)
(A.4)
Trong trường hợp một phía, a/2 trong công thức (A.1) đến (A.4) được thay bằng a.
Phụ lục B
(tham khảo)
Ví dụ
B.1 Ví dụ 1
Dây điện dùng cho thiết bị nhỏ được uốn cong bằng máy thử cho đến khi hỏng. Phép thử mô phỏng sử dụng thực tế, trong các điều kiện tăng cường. 24 lần hỏng, tính bằng giờ, được cho dưới đây; bảy lần trong số đó bị mất theo dõi và được đánh dấu bằng dấu sao1):
| 57,5 | 77,8 | 88,0 | 96,9 | 98,4 | 100,3 |
| 100,8 | 102,1 | 103,3 | 103,4 | 105,3 | 105,4 |
| 122,6 | 139,3 | 143,9 | 148,0 | 151,3 | 161,1* |
| 161,2* | 161,2* | 162,4* | 162,7* | 163,1* | 176,8* |
Yêu cầu ước lượng trung vị và giới hạn tin cậy dưới đối với trung vị đó ở mức tin cậy 95 %.
Ước lượng điểm của trung vị thời gian sống là
![]() = (x[12] + x[13])/2
= (x[12] + x[13])/2
= (105,4 + 122,6)/2
= 114,0 h
Giới hạn tin cậy một phía dưới đối với trung vị có mức tin cậy 95 % thu được bằng cách lấy giá trị k từ Bảng 1 cho n = 24 và mức tin cậy 95 % đối với trường hợp một phía, sau đó tìm thời điểm hỏng thứ k trong danh mục ở trên.
Giá trị từ Bảng 1 là k = 8 và x[8] = 102,1, vì thế có thể khẳng định với độ tin cậy 95 % là trung vị tổng thể không nhỏ hơn 102,1 h.
CHÚ THÍCH: Có thể ước lượng trung vị và giới hạn dưới của khoảng tin cậy mà không cần theo dõi giá trị lớn nhất trong mẫu.
Việc tính toán trung vị được trình bày dưới dạng bảng ở Mẫu A trang bên. Bản thân các tính toán được trình bày bằng chữ nghiêng.
Mẫu A - Tính toán ước lượng trung vị
| Mẫu để trống |
| Mẫu đã điền |
| Xác định dữ liệu Dữ liệu và quy trình quan trắc:
Đơn vị: Ghi chú:
|
| Xác định dữ liệu Dữ liệu và quy trình quan trắc: Thời gian đến khi hỏng của 24 dây điện, được uốn bằng máy thử. Phép thử mô phỏng sử dụng thực tế nhưng điều kiện tăng cường. Đơn vị: Giờ Ghi chú: Bảy thời gian dài nhất đến khi hỏng bị mất theo dõi. Vì con số này ít hơn một nửa số lần nên vẫn có thể tính được trung vị. |
| Thao tác chuẩn bị Sắp xếp các giá trị quan trắc được theo thứ tự tăng dần, nghĩa là x[1], x[2], …, x[n] |
| Thao tác chuẩn bị Sắp xếp các giá trị quan trắc được theo thứ tự tăng dần, nghĩa là x[1], x[2], …., x[n] |
| Thông tin yêu cầu Cỡ mẫu, n: n = a) Cỡ mẫu lẻ: □ b) Cỡ mẫu chẵn: □ |
| Thông tin yêu cầu Cỡ mẫu, n: n = 24 a) Cỡ mẫu lẻ: □ b) Cỡ mẫu chẵn: S |
| Tính toán ban đầu yêu cầu Đối với a) m = (n + 1)/2 : m = Đối với b) m = n/2 : m = |
| Tính toán ban đầu yêu cầu Đối với a) m = (n + 1)/2 : m = Đối với b) m = n/2: m = 12 |
| Tính toán trung vị mẫu, Đối với a), Đối với b), x[m] = x[m+1] =
|
| Tính toán trung vị mẫu, Đối với a), Đối với b), x[m] = 105,4 x[m+1] = 122,6
|
| Kết quả Trung vị mẫu (ước lượng của trung vị tổng thể) là
|
| Kết quả Trung vị mẫu (ước lượng của trung vị tổng thể) là |
B.2 Ví dụ 2
Độ bền kéo đứt tính bằng niutơn (N) của 120 đoạn sợi ni lông được cho dưới đây, sắp xếp theo thứ tự tăng dần theo các hàng:
| 31,3 | 33,3 | 33,5 | 35,6 | 36,0 | 36,2 | 36,5 | 37,5 | 37,8 | 37,9 | 38,8 | 39,1 | 40,3 | 40,4 | 40,8 |
| 41,0 | 41,8 | 42,4 | 42,9 | 43,1 | 43,2 | 43,5 | 43,9 | 43,9 | 44,0 | 44,2 | 44,2 | 44,5 | 44,7 | 44,7 |
| 45,0 | 45,6 | 46,0 | 46,0 | 46,1 | 46,1 | 46,3 | 46,3 | 46,3 | 46,4 | 46,5 | 46,7 | 47,1 | 47,1 | 47,1 |
| 47,2 | 47,3 | 47,4 | 47,5 | 47,5 | 47,8 | 47,8 | 47,9 | 47,9 | 48,0 | 48,0 | 48,2 | 48,2 | 48,3 | 48,3 |
| 48,3 | 48,5 | 48,6 | 48,6 | 48,6 | 48,6 | 48,8 | 48,9 | 48,9 | 48,9 | 49,0 | 49,0 | 49,1 | 49,1 | 49,1 |
| 49,1 | 49,2 | 49,2 | 49,3 | 49,4 | 49,4 | 49,4 | 49,4 | 49,5 | 49,5 | 49,6 | 49,7 | 49,9 | 49,9 | 50,0 |
| 50,1 | 50,2 | 50,2 | 50,3 | 50,3 | 50,3 | 50,5 | 50,7 | 50,8 | 50,9 | 50,9 | 51,0 | 51,0 | 51,2 | 51,4 |
| 51,4 | 51,4 | 51,6 | 51,6 | 51,8 | 52,0 | 52,2 | 52,2 | 52,4 | 52,5 | 52,6 | 52,8 | 52,9 | 53,2 | 53,3 |
Cần tính ước lượng điểm của trung vị độ bền kéo đứt và tính khoảng tin cậy hai phía ở mức tin cậy 99 %.
Ước lượng điểm của trung vị độ bền kéo đứt là
![]() = (x[60] + x[61])/2 = (48,3 + 48,3) / 2 = 48,3 N
= (x[60] + x[61])/2 = (48,3 + 48,3) / 2 = 48,3 N
Đối với n > 100, Bảng 1 và Bảng 2 không cung cấp giá trị k thích hợp cho các giới hạn tin cậy. Vì yêu cầu giới hạn tin cậy hai phía nên công thức (1) được sử dụng kết hợp với Bảng 4. Giá trị của u và c đối với mức tin cậy 99 % được lấy từ Bảng 4 là u = 2,575 829 30 và c = 1,74. Thay vào công thức (1) với n = 120 được y = 46,448. Lấy phần nguyên của 46,448 được k = 46.
Do đó, khoảng tin cậy hai phía 99 % trên trung vị tổng thể thời gian sửa là
(x[k], x(n-k+1]) = (x[46], x[75]) = (47,2; 49,1) N
Do đó, có thể khẳng định với độ tin cậy ít nhất 99 % là trung vị tổng thể độ bền kéo đứt nằm trong khoảng (47,2; 49,1) N.
Tính toán khoảng tin cậy được trình bày dưới dạng bảng trong Mẫu B với các tính toán thể hiện bằng chữ in nghiêng.
Mẫu B - Tính toán khoảng tin cậy đối với trung vị
| Mẫu để trống |
| Mẫu đã điền |
| Xác định dữ liệu Dữ liệu và quy trình quan trắc:
Đơn vị: Ghi chú: |
| Xác định dữ liệu Dữ liệu và quy trình quan trắc: Độ bền kéo đứt của 120 đoạn sợi ni lông. Đơn vị: Niutơn Ghi chú: Khoảng tin cậy hai phía yêu cầu ở mức tin cậy 99 %. |
| Thao tác chuẩn bị Sắp xếp các giá trị quan trắc được theo thứ tự tăng dần, nghĩa là x[1], x[2], …, x[n] |
| Thao tác chuẩn bị Sắp xếp các giá trị quan trắc được theo thứ tự tăng dần, nghĩa là x[1], x[2], …., x[n] |
| Thông tin yêu cầu Cỡ mẫu, n: n = Mức tin cậy C: C = % a) Khoảng một phía n ≤ 100: □ b) Khoảng hai phía n ≤ 100: □ c) Khoảng một phía n > 100: □ d) Khoảng hai phía n > 100: □ Đối với a) hoặc c) có giới hạn tin cậy trên, giới hạn dưới cho x trong tổng thể được yêu cầu: a = Đối với a) hoặc c) có giới hạn tin cậy dưới, giới hạn trên cho x trong tổng thể được yêu cầu: b = |
| Thông tin yêu cầu Cỡ mẫu, n: n = 120 Mức tin cậy C: C = 99 % a) Khoảng một phía n ≤ 100: □ b) Khoảng hai phía n ≤ 100: □ c) Khoảng một phía n > 100: □ đ) Khoảng hai phía n > 100: S Đối với a) hoặc c) có giới hạn tin cậy trên, giới hạn dưới cho x trong tổng thể được yêu cầu: a = Đối với a) hoặc c) có giới hạn tin cậy dưới, giới hạn trên cho x trong tổng thể được yêu cầu: b = |
| Xác định k Đối với a), tìm k từ Bảng 1: k = Đối với b), tìm k từ Bảng 2: k = Đối với c), tìm u và c từ Bảng 3: u = c = Đối với d), tìm u và c từ Bảng 4: u = c = Đối với c) hoặc d), tính y từ công thức (1): y = sau đó tính k là phần nguyên của y: k = |
| Xác định k Đối với a), tìm k từ Bảng 1: k = Đối với b), tìm k từ Bảng 2: k = Đối với c), tìm u và c từ Bảng 3: u = c = Đối với d), tìm u và c từ Bảng 4: u = 2,575 829 30 c = 1,74 Đối với c) hoặc d), tính y từ công thức (1): y = 46,448 sau đó tính k là phần nguyên của y: k = 46 |
| Xác định giới hạn tin cậy T1 và/hoặc T2 Đối với a) hoặc c) với giới hạn dưới, và đối với b) hoặc d), đặt T1, = x[k] T1 = Đối với a) hoặc c) với giới hạn trên, và đối với b) hoặc d), tính m = n - k + 1: m = rồi đặt T2 = x[m] : T2 = |
| Xác định giới hạn tin cậy T1 và/hoặc T2 Đối với a) hoặc c) với giới hạn dưới, và đối với b) hoặc d), đặt T1 = x[k] T1 = 47,2 Đối với a) hoặc c) với giới hạn trên, và đối với b) hoặc d), tính m = n - k + 1: m = 75 rồi đặt T2 = x[m]: T2 = 49,1 |
| Kết quả Đối với giới hạn tin cậy dưới đơn, C = % khoảng tin cậy đối với trung vị tổng thể là [T1, b) = [ , ]. Đối với giới hạn tin cậy trên đơn, C = % khoảng tin cậy đối với trung vị tổng thể là [a, T2)= [ , ]. Đối với giới hạn tin cậy hai phía, C = % khoảng tin cậy đối xứng đối với trung vị tổng thể là [T1, T2) = [ , ]. |
| Kết quả Đối với giới hạn tin cậy dưới đơn, C = % khoảng tin cậy đối với trung vị tổng thể là [T1, b) = [ , ]. Đối với giới hạn tin cậy trên đơn, C = % khoảng tin cậy đối với trung vị tổng thể là [a, T2) = [ , ]. Đối với giới hạn tin cậy hai phía, C = 99 % khoảng tin cậy đối xứng đối với trung vị tổng thể là [T1, T2) = [47, 2, 49, 1]. |
MỤC LỤC
Lời nói đầu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ, định nghĩa và ký hiệu
3.1. Thuật ngữ và định nghĩa
3.2. Ký hiệu
4. Khả năng áp dụng
5. Ước lượng điểm
6. Khoảng tin cậy
6.1. Quy định chung
6.2. Phương pháp truyền thống
6.3. Mẫu nhỏ (5 ≤ n ≤ 100)
6.4. Mẫu lớn (n > 100)
Phụ lục A (tham khảo) Phương pháp truyền thống xác định giới hạn tin cậy đối với trung vị
Phụ lục B (tham khảo) Ví dụ
1) Khi cá thể bị loại khỏi phép thử mà không bị hỏng, lần thử này được đề cập là "lần bị mất theo dõi".
Bạn chưa Đăng nhập thành viên.
Đây là tiện ích dành cho tài khoản thành viên. Vui lòng Đăng nhập để xem chi tiết. Nếu chưa có tài khoản, vui lòng Đăng ký tại đây!
 Tiêu chuẩn Việt Nam TCVN 8006-7:2013 PDF (Bản có dấu đỏ)
Tiêu chuẩn Việt Nam TCVN 8006-7:2013 PDF (Bản có dấu đỏ) Tiêu chuẩn Việt Nam TCVN 8006-7:2013 DOC (Bản Word)
Tiêu chuẩn Việt Nam TCVN 8006-7:2013 DOC (Bản Word)