- Tổng quan
- Nội dung
- Tiêu chuẩn liên quan
- Lược đồ
- Tải về
Tiêu chuẩn Quốc gia TCVN 11367-2:2016 ISO/IEC 18033-2:2006 Công nghệ thông tin-Các kỹ thuật an toàn-Thuật toán mật mã-Phần 2: Mật mã phi đối xứng
| Số hiệu: | TCVN 11367-2:2016 | Loại văn bản: | Tiêu chuẩn Việt Nam |
| Cơ quan ban hành: | Bộ Khoa học và Công nghệ | Lĩnh vực: | Thông tin-Truyền thông , Khoa học-Công nghệ |
|
Ngày ban hành:
Ngày ban hành là ngày, tháng, năm văn bản được thông qua hoặc ký ban hành.
|
07/07/2016 |
Hiệu lực:
|
Đã biết
|
| Người ký: | Đang cập nhật |
Tình trạng hiệu lực:
Cho biết trạng thái hiệu lực của văn bản đang tra cứu: Chưa áp dụng, Còn hiệu lực, Hết hiệu lực, Hết hiệu lực 1 phần; Đã sửa đổi, Đính chính hay Không còn phù hợp,...
|
Đã biết
|
TÓM TẮT TIÊU CHUẨN VIỆT NAM TCVN 11367-2:2016
Nội dung tóm tắt đang được cập nhật, Quý khách vui lòng quay lại sau!
Tải tiêu chuẩn Việt Nam TCVN 11367-2:2016
TIÊU CHUẨN QUỐC GIA
TCVN 11367-2:2016
ISO/IEC 18033-2:2006
CÔNG NGHỆ THÔNG TIN - CÁC KỸ THUẬT AN TOÀN - THUẬT TOÁN MẬT MÃ - PHẦN 2: MẬT MÃ PHI ĐỐI XỨNG
Information technology - Security techniques - Encryption algorithms - Part 2: Asymmetric ciphers
Lời nói đầu
TCVN 11367-2:2016 hoàn toàn tương đương với ISO/IEC 18033-2:2006.
TCVN 11367-2:2016 do Cục Quản lý mật mã dân sự và Kiểm định sản phẩm mật mã biên soạn, Ban Cơ yếu Chính phủ đề nghị, Tổng cục Tiêu chuẩn Đo lường Chất lượng thẩm định, Bộ Khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 11367 Công nghệ thông tin - Các kỹ thuật an toàn - Thuật toán mật mã gồm 04 phần:
- TCVN 11367-1:2016 (ISO/IEC 18033-1:2015) Công nghệ thông tin - Các kỹ thuật an toàn - Thuật toán mật mã - Phần 1: Tổng quan.
- TCVN 11367-2:2016 (ISO/IEC 18033-2:2006) Công nghệ thông tin - Các kỹ thuật an toàn - Thuật toán mật mã - Phần 2: Mật mã phi đối xứng.
- TCVN 11367-3:2016 (ISO/IEC 18033-3:2010) Công nghệ thông tin - Các kỹ thuật an toàn - Thuật toán mật mã - Phần 3: Mã khối.
- TCVN 11367-4:2016 (ISO/IEC 18033-4:2011) Công nghệ thông tin - Các kỹ thuật an toàn - Thuật toán mật mã - Phần 4: Mã dòng.
Giới thiệu
Tổ chức tiêu chuẩn hóa quốc tế (ISO) và Ủy ban kỹ thuật điện quốc tế (IEC) hướng tới thực tế việc tuân thủ tiêu chuẩn này có thể liên quan tới việc sử dụng các bằng sáng chế
ISO và IEC không liên quan đến các bằng chứng, tính hợp lệ và phạm vi áp dụng của các bản quyền sáng chế này. Người sở hữu bản quyền sáng chế phải tự đảm bảo ISO và IEC rằng họ sẵn sàng đàm phán giấy phép theo các điều khoản và không phân biệt một cách hợp lý và các điều kiện với người yêu cầu trên toàn thế giới. Trong khía cạnh này, tuyên bố của người sáng chế phải được đăng ký với ISO và IEC. Thông tin có thể tìm được từ:
ISO/IEC JTC 1/SC 27 Standing Document 8 (SDH) “Patent Information''
Tài liệu hiện hành 8 (SD8) được công bố công khai tại: http://www.ni.din.de/sc27
Chú ý rằng khả năng một số yếu tố của tiêu chuẩn này có thể là đối tượng của bản quyền sáng chế khác với những điều đã xác định ở trên. ISO và IEC sẽ không chịu trách nhiệm xác định bất kỳ hoặc tất cả các bản quyền sáng chế như vậy.
CÔNG NGHỆ THÔNG TIN - CÁC KỸ THUẬT AN TOÀN - THUẬT TOÁN MẬT MÃ - PHẦN 2: MẬT MÃ PHI ĐỐI XỨNG
Information technology - Security techniques - Encryption algorithms - Part 2: Asymmetric ciphers
1. Phạm vi áp dụng
Tiêu chuẩn này đặc tả một số mật mã phi đối xứng. Các đặc tả này quy định các giao diện chức năng và các phương pháp đúng đắn sử dụng các mật mã loại này nói chung, cũng như chính xác hóa chức năng và định dạng bản mã cho một số mật mã phi đối xứng (mặc dù có thể chọn các hệ thống phù hợp và các định dạng khác để lưu trữ và truyền bản mã).
Phụ lục A cung cấp cú pháp ASN.1 cho các định danh đối tượng, các khóa công khai, và các cấu trúc tham số liên kết với thuật toán được đặc tả trong phần này của ISO/IEC 18033.
Tuy nhiên, các đặc tả này không quy định các giao thức thu được một cách tin cậy khóa công khai, để chứng minh việc sở hữu khóa mật, hay để xác nhận khóa công khai hoặc khóa mật; xem ISO/IEC 117700-3 hướng dẫn các vấn đề quản lý khóa.
Các mật mã phi đối xứng được đặc tả trong tiêu chuẩn này (của bộ TCVN 11367 (ISO/IEC 18033)) được chỉ ra tại Điều 7.6.
CHÚ THÍCH Một cách vắn tắt, mật mã phi đối xứng gồm:
- ECIES-HC; PSEC-HC; ACE-HC: Hệ mật lai ghép tổng quát dựa trên mật mã Elgamal;
- RSA-HC: Mật mã lai ghép dựa trên biến đổi RSA;
- RSAES: Lược đồ đệm OAEP dựa trên biến đổi RSA;
- HIME(R): Lược đồ dựa trên tính khó của bài toán phân tích số.
2. Tài liệu viện dẫn
Các tài liệu viện dẫn sau rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với các tài liệu viện dẫn ghi năm công bố thì áp dụng phiên bản được nêu. Đối với các tài liệu viện dẫn không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi, bổ sung (nếu có).
ISO/IEC 9797-1:1999, Information technology - Security techniques - Message Authentication Codes (MACs) - Part 1: Machanisms using a block cipher
ISO/IEC 9797-2:2002, Information technology - Security techniques - Message Authentication Codes (MACs) - Part 2: Machanisms using a dedicated hash functions
ISO/IEC 10118-2:2000, Information technology - Security techniques - Hash functions - Part 2: hash functions using an n-block cipher
ISO/IEC 10118-3:2004, Information technology - Security techniques - Hash functions - Part 3: dedicated hash functions
ISO/IEC 18033-3:2005, Information technology - Security techniques - Encryption algorithms - Part 3: blocks ciphers
3. Định nghĩa
Trong tiêu chuẩn này áp dụng các thuật ngữ và định nghĩa dưới đây:
CHÚ THÍCH Trong tiêu chuẩn này, ở những nơi phù hợp các tham chiếu tiếp theo được đưa ra trong các Điều mà chứa những định nghĩa và/hoặc soạn thảo chi tiết hơn.
3.1. Mật mã phi đối xứng (asymmetric cipher)
Hệ thống dựa vào các kỹ thuật mật mã phi đối xứng, ở đó phép biến đổi khóa công khai được sử dụng để mã hóa và phép biến đổi khóa riêng dùng để giải mã.
[ISO/IEC 9798-1:2010, 3.2]
CHÚ THÍCH Xem Điều 7.
3.2. Kỹ thuật mật mã phi đối xứng (asymmetric cryptigraphic technique)
Kỹ thuật mật mã phi đối xứng sử dụng hai phép biến đổi liên quan đến nhau, phép biến đổi công khai (được xác định bởi khóa công khai) và biến đổi mật (được xác định bởi khóa mật). Cả hai phép biến đổi này có tính chất là cho biết phép biến đổi công khai, về mặt tính toán không thể có khả năng xác định được phép biến đổi bí mật.
[ISO/IEC 11770-1:1996]
3.3. Cặp khóa phi đối xứng (asymmetric key pair)
Cặp khóa liên quan với nhau, khóa công khai và khóa bí mật, ở đây khóa công khai xác định phép biến đổi công khai, khóa bí mật xác định phép biến đổi bí mật
[ISO/IEC 9798-1:1977]
CHÚ THÍCH Xem Điều 7, 8.1.
3.4. Bit (bít)
Một trong hai ký hiệu ‘0’ và ‘1'
CHÚ THÍCH Xem Điều 5.2.1.
3.5. Xâu bit (bit string)
Dãy các bit
CHÚ THÍCH Xem Điều 5.2.1.
3.6. Khối (block)
Xâu bit có độ dài xác định
[ISO/IEC 18033-1]
CHÚ THÍCH Trong phần này của ISO/IEC 18033, khối được giới hạn là xâu bộ tám (được minh họa một cách tự nhiên như những xâu bit).
3.7. Mã khối (block cipher)
Mã đối xứng với tính chất là thuật toán mã hóa thao tác trên các khối của bản rõ, nghĩa là trên xâu bit có độ dài xác định, kết quả cho ra khối bản mã
[ISO/IEC 18033-1]
CHÚ THÍCH 1 Xem Điều 6.4.
CHÚ THÍCH 2 Trong phần này của ISO/IEC 18033, các khối của bản rõ/ bản mã chỉ giới hạn là các xâu bộ tám (được minh họa một cách tự nhiên như những xâu bit).
3.8. Mật mã (cipher)
Kỹ thuật mật mã dùng để bảo mật dữ liệu, bao gồm từ ba quá trình thành phần: thuật toán mã hóa, thuật toán giải mã, phương pháp tạo khóa
[ISO/IEC 18033-1]
3.9. Bản mã (cipher text)
Dữ liệu được biến đổi để che giấu nội dung thông tin trong đó
[ISO/IEC 10116:1997]
3.10. Nhóm cụ thể (concrete group)
Sự mô tả dưới dạng tường minh nhóm abel hữu hạn, cùng với các thuật toán để thực thi các phép toán trên nhóm và mã hóa, giải mã các phần tử nhóm dưới dạng xâu octet
CHÚ THÍCH Xem Điều 10.1.
3.11. Hàm băm mật mã (cryptographic hash function)
Hàm ánh xạ các xâu bộ tám có độ dài bất kỳ vào xâu bộ tám có độ dài cố định, sao cho bằng tính toán không thể tìm ra mối quan hệ giữa đầu vào và đầu ra, và sao cho, cho trước một phần đầu ra, nhưng không cho trước đầu vào, bằng tính toán không thể đoán được bất kỳ bit nào của phần đầu ra còn lại. Yêu cầu chính xác về độ an toàn phụ thuộc vào ứng dụng.
CHÚ THÍCH Xem Điều 6.1.
3.12. Cơ chế bọc dữ liệu (data encapsulation mechanism)
Cơ chế mật mã dựa trên kỹ thuật mật mã đối xứng, bảo vệ tính bí mật và tính toàn vẹn của dữ liệu
CHÚ THÍCH Xem Điều 8.2.
3.13. Giải mã (decryption)
Ngược với phép mã hóa tương ứng
[ISO/IEC 11770-1:1996]
3.14. Thuật toán giải mã (decryption algorithm)
Quá trình biến đổi bản mã thành bản rõ
[ISO/IEC 18033-1]
3.15. Mã hóa (encryption)
Phép biến đổi khả nghịch dữ liệu bằng thuật toán mật mã để tạo ra bản mã, nghĩa là che giấu nội dung thông tin của dữ liệu
[ISO/IEC 9797-1]
3.16. Trường hữu hạn cho dưới dạng tường minh (explicitly given finite field)
Trường hữu hạn được biểu diễn dưới dạng tường minh, theo thuật ngữ các đặc trưng của nó và một bảng phép nhân làm cơ sở trên một trường nguyên tố
CHÚ THÍCH Xem điều 5.3.
3.17. Thuật toán mã hóa (encryption algorithm)
Quá trình biến đổi bản rõ thành bản mã [ISO/IEC 18033-1]
3.18. Tùy chọn mã hóa (encryption option)
Tùy chọn sao cho có thể được chuyền đến thuật toán mã hóa của hệ mật phi đối xứng, hoặc của cơ chế bọc khóa, để kiểm soát việc định dạng bản mã đầu ra
CHÚ THÍCH Xem điều 7.8.1.
3.19. Trường (field)
Khái niệm toán học của trường, tức là một tập hợp các phần tử cùng với các phép toán hai ngôi là phép cộng và phép nhân trên tập đó, sao cho thỏa mãn các tiên đề về trường
3.20. Nhóm abel hữu hạn (finite abelian group)
Nhóm với tính chất là tập hợp cơ sở gồm hữu hạn phần tử và phép toán hai ngôi cơ sở trên đó có tính giao hoán
3.21. Trường hữu hạn (finite group)
Trường với tập hợp cơ sở của nó là hữu hạn
3.22. Nhóm (group)
Khái niệm toán học về nhóm, tức tập hợp các phần tử với phép toán nhị phân trên tập đó thỏa mãn các tiên đề thông thường về nhóm
3.23. Hệ mật lai ghép (hybird cipher)
Mật mã phi đối xứng kết hợp cả kỹ thuật mật mã phi đối xứng và đối xứng
3.24. Khóa (key)
Dãy các ký hiệu điều khiển hoạt động của phép biến đổi mật mã (ví dụ, phép mã hóa, giải mã)
[ISO/IEC 11770-1:1996]
3.25. Hàm dẫn xuất khóa (key derivation function)
Hàm ánh xạ xâu bộ tám có độ dài bất kỳ thành xâu bộ tám có độ dài xác định, sao cho bằng tính toán không thể tìm ra mối quan hệ giữa đầu vào và đầu ra và sao cho nếu biết một phần đầu ra, nhưng không biết đầu vào, hoàn toàn không có khả năng bằng tính toán, đoán được bất kỳ bit nào của phần đầu ra còn lại.
CHÚ THÍCH Xem Điều 6.2.
3.26. Cơ chế bọc khóa (key encapsulation mechanism)
Tương tự mật mã phi đối xứng, nhưng thuật toán mã hóa nhận đầu vào là khóa công khai, tạo ra khóa bí mật và mã hóa khóa bí mật đó
CHÚ THÍCH Xem Điều 8.1.
3.27. Thuật toán tạo khóa (key generation algorithm)
Phương pháp tạo cặp khóa phi đối xứng
CHÚ THÍCH Xem Điều 7, 8.1.
3.28. Nhãn (label)
Xâu bộ tám là đầu vào của cả thuật toán mã hóa và giải mã trong hệ mật phi đối xứng, và đầu vào của cơ chế đóng gói dữ liệu. Nhãn là thông tin công khai được gắn vào bản mã theo một cách không thể thay đổi được
CHÚ THÍCH Xem Điều 7, 8.2.
3.29. Độ dài (length)
Độ dài của xâu các chữ số hay biểu diễn một số nguyên
Cụ thể:
(1) Độ dài của xâu bit là số bit của xâu
CHÚ THÍCH Xem Điều 5.2.1.
(2) Độ dài của xâu bộ tám là số lượng octet của xâu
CHÚ THÍCH Xem Điều 5.2.2.
(3) Độ dài của số nguyên không âm n là số bit trong biểu diễn nhị phân của n, nghĩa là dlog2(n +1).
CHÚ THÍCH Xem Điều 5.2.4.
(4) Độ dài octet của số nguyên không âm n là số lượng chữ số trong biểu diễn của n theo cơ số 256, tức dlog256(n +1).
CHÚ THÍCH Xem Điều 5.2.4.
3.30. Mã xác thực thông báo (message authentication code) (MAC)
Xâu bit là đầu ra của thuật toán MAC
[ISO/IEC 9797-1]
CHÚ THÍCH 1 Xem Điều 6.3.
CHÚ THÍCH 2 Trong phần này của ISO/IEC 18033, MAC được hạn chế là xâu bộ tám (được minh họa một cách tự nhiên như một xâu bit).
3.31. Thuật toán MAC (MAC algorithm)
Thuật toán tính hàm là ánh xạ các xâu bit và khóa bí mật vào các xâu bit có độ dài cố định, thỏa mãn hai tính chất sau:
- Với khóa và xâu đầu vào bất kỳ, có thể tính hàm một cách hiệu quả;
- Với khóa cố định bất kỳ và không biết trước khóa, bằng tính toán không có khả năng tính được giá trị hàm tại bất kỳ xâu đầu vào mới nào và không biết trước khóa không thể tính được giá trị hàm tại bất kỳ xâu đầu vào mới nào, thậm chí cho biết tập hợp các xâu đầu vào và giá trị tương ứng của hàm, trong đó giá trị của đầu vào thứ i có thể chọn sau khi quan sát i -1 giá trị đầu vào của hàm.
[ISO/IEC 9797-1]
CHÚ THÍCH 1 Xem Điều 6.3.
CHÚ THÍCH 2 Trong phần này của ISO/IEC 18033, xâu đầu và đầu ra chỉ hạn chế là những xâu bộ tám (được minh họa một cách tự nhiên như những xâu bit).
3.32. Bộ tám (octet)
Xâu bit có độ dài bằng 8
CHÚ THÍCH Xem Điều 5.2.2.
3.33. Xâu bộ tám (octet string)
Dãy các octet
CHÚ THÍCH Xem Điều 5.2.2.
CHÚ THÍCH Khi cần, xâu bộ tám có thể được minh họa như một xâu bit bằng cách ghép tất cả các octet thành phần.
3.34. Bản rõ (plaintext)
Thông tin chưa được mã hóa
[ISO/IEC 10116:1997]
3.35. Tập hợp phi tiền tố (prefix free set)
Tập hợp S các xâu bit/octet sao cho không tồn tại các xâu x ≠ y Î S sao cho x là tiền tố của y
3.36. Hàm nguyên thủy [nguyên thủy] (primitive)
Hàm dùng để biến đổi lẫn nhau giữa các dạng dữ liệu
3.37. Khóa bí mật (private key)
Khóa thuộc cặp khóa phi đối xứng của thực thể chỉ được sử dụng bởi thực thể
[ISO/IEC 11770-1:1996]
CHÚ THÍCH xem Điều 7, 8.1.
3.38. Khóa công khai (public key)
Khóa thuộc cặp khóa phi đối xứng có thể được công khai
[ISO/IEC 11770-1:1996]
CHÚ THÍCH Xem Điều 7, 8.1.
3.39. Khóa bí mật (secret key)
Khóa được sử dụng trong kỹ thuật mật mã đối xứng bởi một tập hợp xác định các thực thể
[ISO/IEC 11770-3:1999]
3.40. Mật mã đối xứng (symmetric cipher)
Mật mã dựa trên kỹ thuật mật mã đối xứng, sử dụng cùng một khóa bí mật cho cả thuật toán mã hóa và giải mã
[ISO/IEC 18033-1]
3.41. Các tham số hệ thống (system parameters)
Sự lựa chọn tham số là chọn một lược đồ hoặc một hàm mật mã cụ thể từ một họ các lược đồ hoặc các hàm mật mã
4. Ký hiệu và khái niệm
Trong tiêu chuẩn này áp dụng các ký hiệu và khái niệm dưới đây.
CHÚ THÍCH Trong tiêu chuẩn này, ở những nơi phù hợp các tham chiếu tiếp theo được đưa ra trong các điều mà chứa những định nghĩa và/hoặc soạn thảo chi tiết hơn.
|
| Số nguyên lớn nhất nhỏ hơn hoặc bằng số thực x. Ví dụ:
|
|
| Số nguyên nhỏ nhất lớn hơn hoặc bằng số thực x. Ví dụ:
|
| [a..b] | Khoảng các số nguyên tử a đến b, tính cả a và b |
| [a..b) | Khoảng số nguyên tử a đến b, tính cả a nhưng không tính b |
| |X| | Là lực lượng của X, nếu X là tập hợp hữu hạn; là tập hợp phần tử cơ sở nếu X là nhóm abel hoặc trường hữu hạn; là giá trị tuyệt đối nếu X là số thực; là độ dài của xâu bit hoặc xâu bộ tám nếu X là xâu bit hay xâu bộ tám CHÚ THÍCH Xem Điều 5.2.1, 5.2.2. |
| x Å y | Phép cộng XOR, nếu x và y là xâu bit/octet có cùng độ dài CHÚ THÍCH Xem Điều 5.2.1, 5.2.2. |
| <x1,…,xl> | Xâu bit/octet độ dài l, ở đó x1,x2,….,xl là bit/octet CHÚ THÍCH Xem Điều 5.2.1, 5.2.2. |
| x||y | Phép ghép hai xâu bit/octet x và y, kết quả được xâu với phần đầu là x, phần kế sau là y CHÚ THÍCH Xem Điều 5.2.1 và 5.2.2. |
| gcd(a,b) | Ước số chung lớn nhất của hai số nguyên a và b, nghĩa là số nguyên dương lớn nhất chia hết cho cả a và b (hoặc 0 nếu a = b = 0) |
| a|b | Quan hệ giữa các số nguyên a và b sao cho a chia hết b, tức tồn tại số c để b = ac |
| a = b(mod n) | Quan hệ giữa hai số nguyên a và b sao cho a và b đồng dư theo modulo n, nghĩa là n|a - b., trong đó n là số nguyên khác 0 |
| amod n | Số nguyên duy nhất r Î [0,,…n) sao cho r = a(mod n) |
| a-1 mod n | Số nguyên duy nhất b b Î [0,…,n) sao cho ab = 1(mod n), trong đó a là số nguyên, n số nguyên dương |
| F* | Nhóm nhân các đơn vị của F, trong đó F là trường hữu hạn |
| 0F | Phần tử đồng nhất theo phép cộng (phần tử 0) của trường F. |
| 1F | Phần tử đồng nhất theo phép nhân của trường F. |
| BS2IP | Nguyên thủy biến đổi xâu bit thành số nguyên CHÚ THÍCH Xem Điều 5.2.5. |
| EC2OSP | Nguyên thủy biến đổi đường cong elliptic thành xâu bộ tám (xem Điều 5.4.3) |
| FE2OSP | Nguyên thủy biến đổi phần tử trường thành xâu bộ tám (xem Điều 5.3.1.) |
| FE2IP | Nguyên thủy biến đổi phần tử trường thành số nguyên (xem Điều 5.3.1.) |
| I2BSP | Nguyên thủy biến đổi số nguyên thành xâu bit (xem Điều 5.2.5.) |
| I2OSP | Nguyên thủy biến đổi số nguyên thành xâu bộ tám (xem Điều 5.2.5.) |
| OS2ECP | Nguyên thủy biến đổi xâu bộ tám thành đường cong elliptic (xem Điều 5 4.3) |
| OS2FEP | Nguyên thủy biến đổi xâu bộ tám thành phần tử trường (xem Điều 5.3.1.) |
| OS2IP | Nguyên thủy biến đổi xâu bộ tám thành số nguyên (xem Điều 5.2.5.) |
| Oct(m) | Bộ tám có giá trị nguyên bằng m (xem Điều 5.2.4.) |
| £(n) | Độ dài của số nguyên n tính bằng octet (xem Điều 5.2.5.) |
5. Cơ sở toán học
Điều này mô tả cơ sở toán học được sử dụng trong phần này của ISO/IEC 18033, bao gồm việc trình bày các đối tượng toán học và các nguyên thủy cho biến đổi các dạng dữ liệu.
5.1. Hàm và thuật toán biến đổi
Để tiện cho trình bày, các hàm và các hàm ngẫu nhiên (tức những hàm mà giá trị của nó không chỉ phụ thuộc vào giá trị đầu vào, mà còn vào việc chọn giá trị ngẫu nhiên bổ trợ), thường được xác định ở dạng thuật toán. Ngoại trừ những trường hợp sẽ được nói rõ, người thực thi có thể chọn để khai thác bất kỳ thuật toán tương đương nào (nghĩa là, chọn thuật toán dẫn đến cùng một hàm hoặc hàm ngẫu nhiên). Ngoài ra trong trường hợp hàm ngẫu nhiên, khi mà thuật toán mô tả hàm chỉ ra giá trị ngẫu nhiên, người thực thi có thể sử dụng bộ tạo ngẫu nhiên tương ứng để sinh ra giá trị đó (xem ISO/IEC 18031 với hướng dẫn chi tiết hơn về vấn đề này).
Trong mô tả hàm bằng ngôn ngữ thuật toán, quy ước sau đây được chấp nhận. Một thuật toán có thể tính toán cho ra được giá trị, hoặc ngược lại, có thể thất bại (tức không tính được giá trị). Theo quy ước, nếu thuật toán thất bại, thì trừ khi có ghi chú thêm, một thuật toán khác, sử dụng thuật toán này như một chương trình con, cũng sẽ thất bại.
CHÚ THÍCH Như vậy khái niệm thất bại cũng tương tự như khái niệm “đưa ra ngoại lệ“ (throwing an exception) trong nhiều ngôn ngữ lập trình. Tuy nhiên điều này cũng có thể coi như thuật toán trả về một giá trị đặc biệt, khác với tất cả các giá trị khác được thuật toán đưa ra khi nó không thất bại. Với cách cắt nghĩa như vậy về thất bại, thuật toán vẫn được coi là mô tả hàm. Chi tiết về việc, làm thế nào để thực thi hiệu quả khi thuật toán thất bại, không trình bày ở đây. Tuy nhiên, trong các thực thi thông thường, thuật toán có thể trả về một số dạng “mã lỗi“ cho môi trường thực thi của nó và như vậy nó chỉ ra nguyên nhân thất bại. Cũng cần lưu ý rằng trong một số trường hợp, vì lý do bảo mật, trong khi thực thi cần quan tâm để không để lộ lý do chính xác của một số dạng lỗi nhất định.
5.2. Xâu bit và xâu bộ tám
5.2.1. Bit và xâu bit
Bit là một trong hai ký hiệu ‘0’ và ‘1’.
Xâu bit là một dãy bit. Cho các bit x1,…,xl, <x1,…,xl> là ký hiệu xâu bit độ dài l, gồm các bit xếp theo thứ tự đã cho.
Với xâu bit x = <x1,…,xl>, độ dài l của x được ký hiệu là |x|, và nếu l > 0 thì x1 được gọi là bit đầu, xl được gọi là bit cuối của x.
Với hai xâu bít x và y, x||y ký hiệu kết quả ghép x và y, bởi vậy nếu x = <x1,…,xl>, y = <y1,…,ym> thì x||y = <x1,…,xl,y1,…,ym>
Nếu x và y là hai xâu bit có cùng độ dài l, thì x Å y ký hiệu phép cộng bit XOR của x và y.
Xâu bit có độ dài bằng 0 được gọi là xâu bit rỗng.
CHÚ THÍCH Không có một toán tử nào được định nghĩa dành riêng cho xâu bit, nên nếu x là xâu bit, thì xi không nhất thiết ký hiệu một bit cụ thể của x.
5.2.2. Bộ tám (octet) và xâu bộ tám (octet)
Bộ tám là xâu bit có độ dài bằng 8.
Xâu bộ tám là dãy các bộ tám.
Cho các octet x1,…,xl, thì <x1,…,xl> là ký hiệu xâu bộ tám độ dài l gồm các bộ tám x1,…,xl theo thứ tự đã cho.
Cho xâu bộ tám x = <x1,…,xl>, độ dài l của x được ký hiệu là |x|, nếu / > 0 thì x1 được gọi là bộ tám đầu, xl được gọi là bộ tám cuối của x.
Với hai xâu bộ tám x và y, x||y là ký hiệu kết quả ghép x và y, bởi vậy nếu x = <x1,…,xl>, y = <y1,…,yl> thì x||y = <x1,…,xl,y1,…,ym>
Nếu x và y là hai xâu bộ tám có cùng độ dài, thì x Å y ký hiệu phép cộng bit XOR của x và y.
Xâu bộ tám có độ dài bằng 0 được gọi là xâu bộ tám rỗng.
CHÚ THÍCH 1 Không có toán tử nào được xác định dành riêng cho tập các xâu octet. Do đó nếu x là xâu bộ tám, thi xi không nhất thiết ký hiệu một bộ tám cụ thể của x.
CHÚ THÍCH 2 Để ý rằng, vì bộ tám là xâu bit có độ dài bằng 8, nên nếu x và y là các bộ tám, thì x||y có độ dài bằng 16, nếu <x> và <y> mỗi xâu có độ dài bằng 1 thì <x> II <y> = <x,y> là xâu bộ tám độ dài bằng 2.
5.2.3. Chuyển đổi giữa xâu bit và xâu bộ tám
Các nguyên thủy OS2BSP và BS2OSP chuyển đổi giữa các xâu bit và xâu bộ tám được định nghĩa như sau:
Hàm OS2BSP(x): đầu vào là xâu bộ tám x = <x1,…,xl> và đầu ra là xâu bit y = x1||x2…||xl.
Hàm BS2OSP(y): đầu vào là xâu bit y với độ dài là bội số của 8, đầu ra là xâu bộ tám duy nhất X sao cho y = OS2BSP(x).
5.2.4. Chuyển đổi giữa xâu bit và số nguyên
Các nguyên thủy BS2IP và I2BSP thực hiện chuyển đổi giữa xâu bit và số nguyên được định nghĩa như sau.
Hàm BS2IP (x) ánh xạ xâu bit x vào giá trị nguyên x', như sau. Nếu x = <xl-1,…,x0>, ở đây x0,…xl-1 là các bit, khi đó giá trị x' bằng
![]()
Hàm I2BSP(m, l) nhận đầu vào là hai số nguyên không âm m và l, đầu ra là xâu bit duy nhất x độ dài l sao cho BS2IP(x) = m, nếu tồn tại X như vậy. Ngược lại, hàm thất bại.
Độ dài tính bằng bit của số nguyên không âm n là số bit trong biểu diễn nhị phân của nó, tức
![]()
Để tiện ký hiệu, đặt Oct(m) = I2BSP(m, 8).
CHÚ THÍCH Lưu ý rằng l2BSP(m,l) thất bại khi và chỉ khi độ dài của m tính bằng bít lớn hơn l.
5.2.5. Chuyển đổi giữa xâu bộ tám và số nguyên
Các phép biến đổi nguyên thủy OS2IP và I2OSP chuyển đổi giữa xâu bộ tám và số nguyên được xác định như sau.
Hàm OS2IP(x): đầu vào là xâu bộ tám, đầu ra là số nguyên BS2IP(OS2BSP(x)).
Hàm I2OSP(m,l): đầu vào là hai số nguyên không âm m, l, đầu ra là xâu bộ tám (octet) duy nhất x, độ dài l, thỏa mãn hệ thức OS2IP(x) = m, nếu số nguyên x như vậy tồn tại. Ngược lại, hàm thất bại.
Độ dài tính bằng octet của số nguyên không âm n là số chữ số trong biểu diễn cơ số 256, nghĩa là ![]() ; đại lượng này được ký hiệu là £(n).
; đại lượng này được ký hiệu là £(n).
CHÚ THÍCH Chú ý rằng I2OSP(m, l) thất bại khi và chỉ khi độ dài của m tính bằng bộ tám (octet) lớn hơn l.
5.3. Trường hữu hạn
Điều này mô tả một cấu trúc rất khái quát để mô tả các trường hữu hạn đặc biệt. Trường hữu hạn được xác định bằng cách này được gọi là trường hữu hạn được cho dưới dạng tường minh, và được xác định bởi dữ liệu hiện.
Với trường hữu hạn F có lực lượng q = pe, ở đây p là số nguyên tố và e ≥ 1, dữ liệu hiện của F bao gồm p và e, cùng với “bảng nhân” là ma trận T = (Tij)1≤i,j≤e, trong đó mỗi Tij là bộ e phần tử (e-tuple) từ tập hợp [0,…,p).
Tập hợp các phần tử của trường F là tập hợp tất cả các bộ e phần tử trên [0,…,p). Đầu vào của T được coi như các phần tử của F.
Phép cộng trong F được định nghĩa như sau:
Nếu
a = (a1,…,ae) Î F và b = (b1,…,be) Î F,
Khi đó a + b = c, với
c = (c1,…,ce) và ci = (ai + bi) mod p (1 ≤ i ≤ e).
Phép nhân vô hướng trong F (nhân một phần tử của F với một số thuộc [0,…,p)) như sau:
Nếu
a = (a1,…,ae) Î F và d Î [0…p),
Khi đó d.a = c với
c = (c1,…,ce) và ci = (d.ai) mod p (1 ≤ i ≤ e).
Phép nhân trên trường F được xác định thông qua bảng nhân T, như sau:
Nếu
a = (a1,…,ae) Î F và b = (b1,…,be) Î F,
thì ![]() ,
,
Trong công thức trên cách tích (aibj mod p)Tij được xác định theo quy tắc tích vô hướng đã nêu trên, và chúng được cộng lại theo quy tắc phép cộng trong F. Giả thiết là bảng nhân xác định một cấu trúc đại số thỏa mãn các tiên đề thông thường của trường; nói riêng, tồn tại các phần tử đồng nhất đối với phép cộng và phép nhân (tức phần tử trung hòa và đơn vị), mỗi phần tử của trường có phần tử nghịch đảo đối với phép cộng (phần tử đối) và phần tử nghịch đảo đối với phép nhân.
Nhận thấy rằng phần tử đồng nhất đối với phép cộng của F, ký hiệu là 0F, chính là bộ e phần tử gồm các phần tử 0 và phần tử đồng nhất đối với phép nhân được ký hiệu là 1F, là bộ e phần tử khác không với định dạng chính xác của 1F phụ thuộc vào T.
CHÚ THÍCH 1 Trường F là không gian véc tơ có số chiều là e, xác định trên trường nguyên tố F’, có lực lượng bằng p, với phép nhân vô hướng đã được định nghĩa trên đây. Số nguyên tố p được gọi là đặc số của trường F. Với 1 ≤ i ≤ e, ký hiệu qi là bộ e-phần tử (e-tuple) trên F' sao cho thành phần thứ i của nó là 1 và tất cả thành phần còn lại bằng 0. Các phần tử q1,..,qe tạo thành cơ sở của không gian véc tơ F trên F'. Lưu ý rằng với mọi 1 ≤ i, j ≤ e, ta có qiqj = Tij.
CHÚ THÍCH 2 Với e > 1, có hai kiểu cơ sở cùng được sử dụng trong thực thi các phép toán số học trên trường hữu hạn:
- q1,…qe được gọi là cơ sở đa thức cho F trên F' nếu tồn tại q thuộc F sao cho qi = qe-1 với mọi 1 ≤ i ≤ e. Rõ ràng ta có 1F = qe.
- q1,…qe được gọi cơ sở chuẩn tắc cho F trên F' nếu tồn tại q thuộc F sao cho ![]() với mọi 1 ≤ i ≤ e. Rõ ràng trong trường hợp này, ta có
với mọi 1 ≤ i ≤ e. Rõ ràng trong trường hợp này, ta có ![]() với c Î [1,..,p); Nếu p = 2, khi đó chỉ có một lựa chọn duy nhất cho c là 1; hơn nữa luôn luôn có thể chọn cơ sở chuẩn tắc với c = 1.
với c Î [1,..,p); Nếu p = 2, khi đó chỉ có một lựa chọn duy nhất cho c là 1; hơn nữa luôn luôn có thể chọn cơ sở chuẩn tắc với c = 1.
CHÚ THÍCH 3 Định nghĩa trường hữu hạn dưới dạng tường minh được trích dẫn từ [23].
5.3.1. Chuyển đổi giữa xâu bộ tám và số nguyên/trường hữu hạn
Các phép biến đổi nguyên thủy OS2FEPF và FE2OSPF giữa xâu bộ tám và các phần tử của trường hữu hạn được cho dưới dạng tường minh F, cũng như phép biến đổi nguyên thủy FE2IPF chuyển đổi các phần tử của F thành số nguyên, được định nghĩa như sau.
Hàm FE2IPF ánh xạ phần tử a Î F vào giá trị nguyên a', như sau. Nếu lực lượng của F là q = pe, ở đây p là số nguyên tố và e ≥ 1, khi đó phần tử a của trường F là bộ e phần tử (a1,…ae), ai Î [0,…,p), 1 ≤ i ≤ e và giá trị a' được xác định theo công thức:
![]()
Hàm FE2OSPF(a) nhận đầu vào là phần tử a của trường, đầu ra là xâu bộ tám I2OSP(a',l), a' = FE2OSPF(a) và l là độ dài tính bằng bộ tám của |F| - 1, nghĩa là ![]() . Như vậy đầu ra của FE2OSPF(a) luôn là xâu bộ tám có độ dài chính xác bằng
. Như vậy đầu ra của FE2OSPF(a) luôn là xâu bộ tám có độ dài chính xác bằng ![]() .
.
Hàm OS2FEPF(x) nhận đầu vào là xâu bộ tám x, đầu ra (duy nhất) là phần tử trường a Î F sao cho FE2OSPF(a) = x, nếu tồn tại a như thế, và ngược lại thì thất bại. Lưu ý rằng OS2FEPF(x) thất bại khi và chỉ khi hoặc x không có độ dài đúng bằng ![]() , hoặc OS2IP(x) ≥ |F|.
, hoặc OS2IP(x) ≥ |F|.
5.4. Đường cong elliptic
Đường cong elliptic trên trường hữu hạn dạng tường minh là tập hợp các điểm P = (x, y), ở đây x và y là các phần tử của trường F, thỏa mãn phương trình xác định, với "điểm tại vô cùng" được ký hiệu là ![]() . Trong phần này của tiêu chuẩn ISO/IEC-18033, đường cong elliptic E được xác định bởi hai phần tử của trường a,b Î F, các phần tử này được gọi là các hệ số của E.
. Trong phần này của tiêu chuẩn ISO/IEC-18033, đường cong elliptic E được xác định bởi hai phần tử của trường a,b Î F, các phần tử này được gọi là các hệ số của E.
Giả sử P là đặc trưng của trường F.
Nếu p > 3 thì a và b thỏa mãn điều kiện 4a3 + 27b2 ¹ 0F, và mỗi điểm P = (x,y) trên E (khác phần tử ![]() ) thỏa mãn phương trình
) thỏa mãn phương trình
y2 = x3 + ax + b.
Nếu p = 2, thì a và b thỏa mãn điều kiện b ¹ 0F, và mỗi điểm P = (x,y) trên E (khác phần tử ![]() ) thỏa mãn phương trình
) thỏa mãn phương trình
y2 + xy = x3 + ax2 + b.
Nếu p = 3, thì a và b thỏa mãn điều kiện a ¹ 0F và b ¹ 0F, và mỗi điểm P = (x,y) trên E (khác phần tử ![]() ) thỏa mãn phương trình
) thỏa mãn phương trình
y3 = x3 + ax2 + b.
Các điểm nằm trên đường cong elliptic tạo thành nhóm abel, với phần tử không ![]() của E là phần tử trung hòa. Tồn tại những thuật toán hiệu quả để thực thi các phép toán nhóm của đường cong elliptic, tuy nhiên việc thực thi các thuật toán này nằm ngoài phạm vi của phần này của ISO/IEC 18033.
của E là phần tử trung hòa. Tồn tại những thuật toán hiệu quả để thực thi các phép toán nhóm của đường cong elliptic, tuy nhiên việc thực thi các thuật toán này nằm ngoài phạm vi của phần này của ISO/IEC 18033.
CHÚ THÍCH Xem ISO/IEC 15946-1, cũng như [9], để biết thêm thông tin về cách thực thi hiệu quả phép toán nhóm trên đường cong elliptic.
5.4.1. Các điểm nén của đường cong elliptic
Giả sử E là đường cong elliptic trên trường hữu hạn dạng tường minh F, ở đây F có đặc trưng bằng p.
Điểm P ¹ ![]() có thể được biểu diễn dưới dạng nén, không nén và hoặc lai ghép.
có thể được biểu diễn dưới dạng nén, không nén và hoặc lai ghép.
Nếu P = (x,y), thì (x,y) là dạng không nén của P.
Giả sử P = (x,y) là điểm trên đường cong elliptic E. Dạng nén của P là cặp (x,ỹ), ở đây ỹ Î {0,1} được xác định như sau:
- Nếu p ¹ 2 và y = 0F, thì ỹ = 0.
- Nếu p ¹ 2 và y ¹ 0F, thì ỹ = ((y' / pf) mod p) mod 2, ở đây y' = FE2IPF(y) và f là số nguyên không âm lớn nhất sao cho pf|y'.
- Nếu p = 2 và x = 0F thì ỹ = 0.
- Nếu p = 2 và x ¹ 0F thì ỹ = ![]() mod 2, ở đây z = y/x và z' = FE2IPF(y) và f là số nguyên không âm nhỏ nhất thỏa mã điều kiện 2f chia hết FE2IPF(1F).
mod 2, ở đây z = y/x và z' = FE2IPF(y) và f là số nguyên không âm nhỏ nhất thỏa mã điều kiện 2f chia hết FE2IPF(1F).
Dạng lai ghép của P = (x,y) là bộ ba (x,ỹ,y) với ỹ được xác định như ở Điều trước.
5.4.2. Các thuật toán giải nén điểm
Tồn tại các thuật toán hiệu quả giải nén điểm, tức là tính ỹ từ (x, ỹ). Dưới đây sẽ mô tả vắn tắt các thuật toán đó.
- Giả sử p ¹ 2 và (x,ỹ) là dạng nén của (x,y). Điểm (x,y) thỏa mãn phương trình y2 = f(x) với f(x) là đa thức trên F. Nếu f(x) = 0F, thì chỉ có một khả năng chọn y, chính là y = 0F. Ngược lại, nếu f(x) ¹ 0 thì có hai khả năng chọn y, các khả năng này chỉ khác nhau về dấu, việc chọn đúng được xác định bởi ỹ. Có hai thuật toán tính căn bậc hai trên trường hữu hạn được biết đến nhiều, và do đó hai lựa chọn y dễ dàng tính được.
- Giả sử p = 2 và (x,ỹ) là dạng nén của (x,y). Các điểm (x,y) thỏa mãn phương trình y2 + xy = x3 + ax2 + b. Nếu x = 0F, khi đó y2 = b, từ đây y được tính toán dễ dàng và duy nhất. Ngược lại nếu x ¹ 0F khi đó đặt z = y/x, ta có z2 + z = g(x) ở đây g(x) = (x + a + bx-2). Giá trị của y được xác định một cách duy nhất và dễ dàng tính ra được từ các giá trị z và x, do đó chỉ cần tính z. Để tính z, ta lưu ý rằng với x cố định, nếu z là một trong các nghiệm của phương trình z2 + z = g(x), khi đó có đúng một nghiệm khác, chính là z + 1F. Dễ dàng tính được hai giá trị ứng cử viên của z và dễ thấy rằng việc chọn đúng z được xác định bởi ỹ.
5.4.3. Chuyển đổi giữa xâu bộ tám và đường cong elliptic
Các nguyên thủy EC2OSPE và OS2ECPE chuyển đổi giữa các điểm trên đường cong elliptic và xâu bộ tám được xác định như sau.
Giả sử E là đường cong elliptic trên trường hữu hạn được cho ở dạng hiện F.
Hàm EC2OSPE(P, fmt) nhận đầu vào là điểm P trên E và bộ định dạng fmt là một trong các giá trị ký hiệu được nén, không được nén, hoặc lai ghép. Đầu ra là xâu bộ tám EP, được tính như sau:
- Nếu P = ![]() thì EP =
thì EP = ![]() .
.
- Nếu P = (x,y) ¹ ![]() với dạng nén (x,ỹ), khi đó
với dạng nén (x,ỹ), khi đó
EP = ![]() ,
,
ở đây,
- H là bộ tám đơn có dạng Oct(4U + C.(2 + ỹ)), trong đó,
- U = 1 nếu fmt hoặc là dạng không nén hoặc dạng lai ghép, ngược lại U = 0;
- C = 1 nếu fmt hoặc dạng nén hoặc dạng lai ghép, ngược lại C = 0;
- X là xâu bộ tám FE2OSPF(x):
- Y là xâu bộ tám FE2OSPF(y), nếu fmt hoặc dạng không nén hoặc dạng lai ghép; ngược lại y là xâu bộ tám rỗng.
CHÚ THÍCH Nếu (biến) định dạng fmt không ở dạng nén, thi không cần tính giá trị ỹ .
Hàm OS2ECPE(EP) nhận đầu vào là xâu bộ tám EP. Nếu tồn tại điểm P trên đường cong elliptic E và (biến) định dạng fmt thỏa mãn EC2OSPE(P, fmt) = EP, khi đó đầu ra của hàm là P (ở dạng không nén), ngược lại-hàm thất bại. Lưu ý rằng điểm P, nếu tồn tại, được xác định duy nhất và do đó hàm OS2ECPE(EP) đã được xác định rõ.
6. Các biến đổi mật mã
Điều này mô tả một số phép biến đổi mật mã sẽ được tham chiếu ở các Điều tiếp theo. Các dạng biến đổi đó là: hàm băm mật mã, hàm dẫn xuất khóa, mã xác thực thông báo, mã khối, và mã đối xứng. Với mỗi dạng biến đổi sẽ đưa ra các đặc trưng đầu ra/đầu vào ngắn gọn, tiếp đó sẽ đặc tả các thực thi cụ thể các phép biến đổi này, chúng được phép sử dụng trong phần này của ISO/IEC18003.
6.1. Các hàm băm mật mã
Hàm băm mật mã là hàm ánh xạ các xâu bộ tám có độ dài thay đổi vào xâu bộ tám có độ dài cố định. Chính xác hơn, hàm băm (hash function) mật mã xác định
- số nguyên dương Hash.Len ký hiệu độ dài đầu ra của hàm băm,
- số nguyên dương Hash.MaxInputLen ký hiệu độ dài lớn nhất của đầu vào hàm băm,
- và hàm Hash.eval ký hiệu bản thân hàm băm, ánh xạ xâu bộ tám có độ dài lớn nhất Hash.MaxInputLen vào xâu bộ tám độ dài Hash.Len.
Việc gọi hàm Hash.eval thất bại khi và chỉ khi độ dài đầu ra vượt quá giá trị Hash.MaxInputLen.
6.1.1. Các hàm băm mật mã cho phép
Với mục đích của phần này của ISO/IEC 18033, các hàm băm mật mã là những hàm được mô tả trong ISO/IEC 10118-2 và ISO/IEC 10118-3 với những quy định sau đây:
- Hàm băm trong ISO/IEC 10118 ánh xạ xâu bit vào xâu bit, trong khi đó trong ISO/IEC 18033 hàm băm ánh xạ xâu bộ tám vào xâu bộ tám. Do đó hàm băm trong ISO/IEC 10118-2 và ISO/IEC 10118-3 được phép áp dụng vào phần này của tiêu chuẩn ISO/IEC 18033, chỉ khi độ dài tính bằng bit của đầu ra là bội số của 8, trong trường hợp này ánh xạ giữa các xâu bộ tám và xâu bit bị tác động bởi các hàm OS2BSP và BS2OSP.
- Ngược lại, nếu như hàm băm trong ISO/IEC 10118 không xác định đối với đầu vào vượt quá độ dài cho trước, thì hàm băm trong phần này của ISO/IEC 18033 được xác định là thất bại đối với những đầu vào như vậy.
6.2. Hàm dẫn xuất khóa
Hàm dẫn xuất khóa là hàm KDF(x,l), nhận đầu vào là xâu bộ tám x và số nguyên l ≥ 0, và đầu ra là xâu bộ tám độ dài l. Xâu x có độ dài bất kỳ, mặc dù trong khi thực thi có thể xác định độ dài cực đại (rất lớn) cho x là kích thước cực đại cho l và thất bại nếu các giới hạn này bị vượt qua.
CHÚ THÍCH Trong một số tài liệu và tiêu chuẩn khác, thuật ngữ “hàm tạo mặt nạ“ ("mask generation function") được sử dụng thay cho "hàm dẫn xuất khóa".
6.2.1. Hàm dẫn xuất khóa được phép
Các hàm dẫn xuất khóa được phép trong phần này của ISO/IEC 18033 là KDF1 được mô tả phía dưới, ở Điều 6.2.2 và KDF2 được mô tả ở Điều 6.2.3.
6.2.2. KDF1
6.2.2.1. Các tham số hệ thống
KDF1 là họ các hàm dẫn xuất khóa được tham số hóa bởi các tham số hệ thống sau đây:
- Hash: hàm băm mật mã được mô tả ở Điều 6.1.
6.2.2.2. Đặc tả
Với xâu bộ tám x và số nguyên không âm l, KDF1(x, l) được xác định cho l bộ tám đầu tiên của xâu Hash.eval (x||I2OSP(0,4)||...|| Hash.eval(x||I2OSP(k -1,4),
ở đây ![]()
CHÚ THÍCH Hàm này sẽ thất bại khi và chỉ khi k > 232 hoặc khi |x|+ 4 >Hash.MaxIputLen.
6.2.3. KDF2
6.2.3.1. Các tham số hệ thống
KDF2 là hộ các hàm dẫn xuất khóa, được tham số bởi các tham số hệ thống sau:
- Hash: hàm băm mật mã được mô tả tại Điều 6.1.
6.2.3.2. Đặc tả
Với xâu bộ tám x và số nguyên không âm l, KDF2 (x,l) được xác định như là bộ tám đầu tiên của xâu
Hash.eval (x||I2OSP(1,4)||...||Hash.eval(x||I2OSP(k,4)).
ở đây ![]()
CHÚ THÍCH 1 Hàm này sẽ thất bại khi và chỉ khi k > 232 hoặc |x|+4>Hash.MaxlnputLen.
CHÚ THÍCH 2 KDF2 cũng giống như KDF1, trừ việc tính từ 1 đến k thay vì từ 0 đến k -1.
6.3. Các thuật toán MAC
Thuật toán xác thực thông báo MA là lược đồ xác định hai số nguyên dương MA.KeyLen, MA. MACLen, cùng hàm MA.eval(k',T), hàm này nhận khóa mật k’ là xâu bộ tám độ dài bằng MA.KeyLen, và xâu bộ tám tùy ý T làm đầu vào và tính đầu ra là xâu bộ tám MAC độ dài MA.MACLen.
Việc thực thi có thể hạn chế giá trị cực đại cho độ dài của T và MA.eval(k',T) sẽ thất bại nếu giới hạn này bị vượt qua.
CHÚ THÍCH Tham khảo Phụ lục B.1 xem thảo luận về các tính chất bảo mật mong muốn của các thuật toán MAC.
6.3.1. Các thuật toán MAC được phép
Với mục đích của phần này của ISO/IEC 18033, các thuật toán MAC được phép được mô tả trong ISO/IEC 9797-1 và ISO/IEC 9797-2, với các quy định sau:
- Đối với các thuật toán MAC được mô tả trong ISO/IEC 9797-1 và ISO/IEC 9797-2, đầu ra là các xâu bit, khóa bí mật và đầu ra là những xâu có độ dài cố định. Bởi vậy, một thuật toán trong ISO/IEC 9797-1 hoặc ISO/IEC 9797-2 được phép áp dụng trong phần này của ISO/IEC 18033 chỉ khi độ dài tính bằng bit của MAC và khóa mật là bội số của 8, trong trường hợp này ánh xạ giữa các xâu bộ tám và các xâu bit bị ảnh hưởng bởi OS2BSP và BS2OSP.
- Nếu các thuật toán trong ISO/IEC 9797-1 và ISO/IEC 9797-2 không xác định đối với đầu vào vượt quá độ dài cho trước, thì thuật toán MAC trong phần này của ISO/IEC 18033, được xác định là thất bại đối với những đầu vào như vậy.
6.4. Mã khối
Mã khối BC đặc tả như sau:
- số nguyên dương BC.KeyLen, là độ dài của khóa mật tính bằng octet,
- số nguyên dương BC. BlockLen, là độ dài tính bằng octet của khối bản mã hoặc bản rõ,
- hàm BC.Encrypt(k,b), nhận đầu vào là khóa bí mật k, với k là xâu bộ tám, độ dài BC.KeyLen và khối bản rõ b là xâu bộ tám độ dài BC.BlockLen, và đầu ra là khối mã b' với b' là xâu bộ tám độ dài BC.BlockLen, và
- hàm BC.Decrypt(k,b'), nhận đầu vào là khóa bí mật là xâu bộ tám, độ dài BC.KeyLen, và khối bản mã b' là xâu bộ tám độ dài BC.BlockLen, và đầu ra là khối bản rõ là xâu bộ tám, độ dài BC.BlockLen.
Với khóa bí mật cố định bất kỳ k, hàm b →BC.Encrypt(k,b) tác động như một phép hoán vị trên tập các xâu bộ tám độ dài BC.BlockLen, và hàm b'→BC.Decrypt(k,b) tác động như một phép hoán vị nghịch đảo.
CHÚ THÍCH Xem thảo luận trong Phụ lục B.2 về tính chất bảo mật mong muốn của mã khối.
6.4.1. Mã khối được phép
Trong phần này của ISO/IEC 18033, mã khối được phép là những mã khối được mô tả trong ISO/IEC 18033-3, với các quy định sau:
- Trong ISO/IEC 18033-3, các khối bản rõ/bản mã và khóa bí mật là những xâu bit có độ dài cố định, còn trong phần này của ISO/IEC 18033, chúng là những xâu bộ tám có độ dài cố định. Bởi vậy, mã khối trong ISO/IEC 18033-3 được phép áp dụng trong phần này của ISO/IEC 18033 chỉ khi độ dài tính bằng bit của các khối bản rõ/bản mã và của khóa bí mật là bội số của 8, trong trường hợp này ánh xạ giữa các xâu bộ tám và xâu bị tác động bởi các hàm OS2OSP và BS2OSP.
6.5. Mã đối xứng
Mã đối xứng SC xác định độ dài khóa SC. KeyLen, cùng với các thuật toán mã hóa, giải mã:
- Thuật toán mã hóa SC.Encrypt(k,M) nhận đầu vào là khóa bí mật k, khóa này là xâu bộ tám độ dài SC.KeyLen và bản rõ M là xâu bộ tám độ dài bất kỳ, đầu ra là bản mã c là xâu bộ tám.
Thuật toán mật mã có thể thất bại, nếu độ dài của M vượt quá một giá trị lớn nào đó, được xác định bởi quá trình thực thi.
- Thuật toán giải mã SC.Decrypt(k,c) nhận đầu vào là khóa bí mật k, khóa này là xâu bộ tám độ dài SC.KeyLen, và bản mã c là xâu bộ tám độ dài bất kỳ, đầu ra là bản rõ M là xâu bộ tám.
Thuật toán giải mã có thể thất bại trong một số tình huống nào đó.
Các thuật toán mã hóa và giải mã là tất định. Đồng thời, đối với tất cả khóa bí mật k và tất cả bản rõ M, nếu M không vượt quá giới hạn độ dài của thuật toán mã hóa và nếu c = SC.Encryt(k,M), thì SC.Decrypt (k, c) không thất bại và SC.Decrypt (k,c) = M.
CHÚ THÍCH Xem thảo luận trong phụ lục B.3 về các tính chất bảo mật mong muốn của mã đối xứng.
6.5.1. Mật mã đối xứng được phép
Mật mã đối xứng được phép sử dụng trong phần này của ISO/IEC 18033 là:
- SC1, được mô tả tại Điều 6.5.2, và
- SC2, được mô tả tại Điều 6.5.3.
6.5.2. SC1
Mã khối đối xứng này đạt được bằng cách sử dụng mã khối ở chế độ CBC (cipher block chaining - xem ISO/IEC 10116), cùng với lược đồ đệm (padding) cụ thể, để bổ sung bản rõ sao cho độ dài của chúng là bội số của kích thước khối của mã khối cơ sở.
6.5.2.1. Các tham số hệ thống
SC1 là họ mã khối đối xứng được tham số hóa bằng các tham số hệ thống sau đây:
- BC: mã khối, được mô tả trong Điều 6.4.
Nói một cách chặt chẽ, cần hạn chế sao cho BC.BlockLen < 256. Và hạn chế này luôn được đáp ứng trên thực tế.
6.5.2.2. Đặc tả
SC1.KeyLen = BC.KeyLen.
Hàm SC1.Encrypt(K,M) làm việc như sau:
a) Đặt PadLen = BC.BlockLen - (|M| mod BC.BlockLen).
b) Giả sử P1 = Oct(padLen).
c) Giả sử P2 là xâu bộ tám được hình thành bằng cách lặp lại octet P1 với tổng số lần lặp bằng PadLen (bởi vậy |P2| = padLen).
d) Giả sử M’ = M||P2.
e) Tạo cú pháp cho M’: M' = ![]()
![]()
![]() , ở đây với 1 ≤ i ≤ l,
, ở đây với 1 ≤ i ≤ l,![]() là xâu bộ tám độ dài BC.BlockLen.
là xâu bộ tám độ dài BC.BlockLen.
f) Giả sử c0 là xâu bộ tám, bao gồm các bản sao BC.BlockLen của octet 0ct(0) và với 1 ≤ i ≤ l, đặt ci = BC. Encrypt(k,![]() Å ci-1).
Å ci-1).
g) Giả sử c = c1 ![]() cl.
cl.
h) Đưa ra c.
Hàm SC1. Decrypt(k,c) làm việc như sau:
a) Nếu |c| không phải là bội số khác không của BC.BlockLen, hàm sẽ thất bại.
b) Tạo cú pháp cho c, c = c1 ![]() cl với 1 ≤ i ≤ l là xâu bộ tám độ dài BC.BlockLen, đồng thời giả sử c0 là xâu bộ tám bao gồm các bản sao BC. BlockLen của Oct(0).
cl với 1 ≤ i ≤ l là xâu bộ tám độ dài BC.BlockLen, đồng thời giả sử c0 là xâu bộ tám bao gồm các bản sao BC. BlockLen của Oct(0).
c) Với 1 ≤ i < l, đặt ![]() = BC.Decrypt(k,ci) Å ci-1.
= BC.Decrypt(k,ci) Å ci-1.
d) Giả sử P1 là octet cuối cùng của ![]() , và giả sử padLen = BS2IP(P1).
, và giả sử padLen = BS2IP(P1).
e) Nếu padLen Ï [1..BC.BlockLen] thì sẽ thất bại.
f) Kiểm tra nếu bộ tám cuối cùng padLen của ![]() bằng hay không; nếu không bằng thì thất bại.
bằng hay không; nếu không bằng thì thất bại.
g) Giả sử M’’l là xâu bộ tám bao gồm từ những octet đầu tiên BC.BlockLen - padlen của ![]() .
.
h) Đặt M - ![]()
![]()
![]()
![]()
i) Đưa ra M.
6.5.3. SC2
6.5.3.1. Các tham số hệ thống
SC2 là họ các mã đối xứng, được tham số hóa bởi các tham số hệ thống sau đây:
- KDF Hàm dẫn xuất khóa được mô tả tại Điều 6.2;
- KeyLen: số nguyên dương.
6.5.3.2. Đặc tả
Giá trị của SC2. KeyLen bằng giá trị của tham số hệ thống KeyLen.
Hàm SC2.Encrypt(k,M) làm việc như sau;
a) Đặt mask = KDF(k,|M|).
b) Đặt c = mask Å M.
c) Đưa ra c
Hàm SC2.Decrypt(k,c) làm việc như sau:
d) Đặt mask = KDF(k, |c|).
e) Đặt M = mask Å c.
f) Đưa ra M.
7. Mật mã phi đối xứng
Mật mã phi đối xứng AC bao gồm từ ba thuật toán:
- Thuật toán tạo khóa AC.KeyGen(), với đầu ra là cặp khóa công khai/khóa bí mật (PK, pk). Cấu trúc của PK và pk phụ thuộc vào mật mã cụ thể.
- Thuật toán mã hóa AC.Encrypt (PK,L,M,opt), nhận đầu vào là khóa công khai, nhãn L, bản rõ M và tùy chọn opt, đầu ra là bản mã C. Lưu ý rằng L, M và C là các xâu bộ tám. Xem thêm Điều 7.2 phía dưới về nhãn. Xem Điều 7.4 để biết thêm về tùy chọn mật mã.
Thuật toán mã hóa có thể thất bại, nếu độ dài L hoặc M vượt quá giới hạn trong thực thi.
- Thuật toán giải mã AC.Decrypt(pk,L,C), nhận đầu vào là khóa riêng pk, nhãn L, bản mã C và đầu ra là bản rõ M.
Thuật toán giải mã có thể thất bại trong một số tình huống nào đấy.
Nhìn chung, các thuật toán tạo khóa, mã hóa là các thuật toán xác suất, còn thuật toán giải mã là thuật toán tất định.
CHÚ THÍCH 1 Mục đích của tất cả mật mã phí đối xứng trong phần này của ISO/IEC18033 là cung cấp độ an toàn thích hợp chống lại kiểu tấn công chọn bản mã thích hợp (được định nghĩa trong [30], và điều này tương đương với khái niệm “khả năng không bị uốn" (“non-malleability"), được định nghĩa trong [17]). Khái niệm an toàn này nhìn chung được cộng đồng nghiên cứu mật mã đánh giá như một hình thức an toàn phù hợp mà mật mã phi đối xứng cần cung cấp. Định nghĩa hình thức của khái niệm an toàn này được trình bày tại phụ lục B.4, và đã được điều chỉnh phù hợp với bản rõ có độ dài thay đổi và vai trò của nhãn; đồng thời cũng định nghĩa một khái niệm yếu hơn một ít về tính an toàn, được gọi là “dễ bị uốn nhẹ" (benign malleability). Khái niệm "dễ bị uốn thích hợp", nếu không phải với tất cả, thì cũng với đại đa số ứng dụng của mật mã phi đối xứng, và một số mật mã phi đối xứng trong phần này của ISO/IEC 18033 chỉ đạt được mức an toàn này.
CHÚ THÍCH 2 Yêu cầu cơ bản của bất kỳ mật mã phi đối xứng là tính đúng đắn: Với bất kỳ cặp khóa công khai/khóa riêng (PK, pk), với cặp bất kỳ nhãn/bản rõ (L,M) sao cho độ dài L, M không vượt quá giới hạn do thực thi quyết định, bất kỳ sự mã hóa bản rõ M với nhãn L và PK được giải mã bằng nhãn L và pk để nhận được bản rõ.
CHÚ THÍCH 3 Một ví dụ mật mã phi đối xứng chứng tỏ yêu cầu trên đây về tính đúng đắn không phải luôn luôn thỏa mãn là mật mã dựa trên RSA với n = pq, p và q là hai số nguyên tố. Thuật toán tạo khóa có thể sử dụng các thuật toán xác suất để kiểm tra liệu p và q có phải là các số nguyên tố không, và thuật toán này có thể đưa ra kết quả sai với xác suất không đáng kể. Nếu xảy ra điều đó, thì thuật toán giải mã có thể không phải là thuật toán nghịch đảo của thuật toán mã hóa.
7.1. Độ dài bản rõ
Một điều quan trọng cần chú ý là, bản rõ có thể có độ dài thay đổi và bất kỳ, mặc dù khi thực thi có thể áp đặt một giới hạn trên (thường là rất lớn) cho độ dài này.
Tuy vậy, có hai dạng mật mã phi đối xứng suy biến, được định nghĩa như sau:
- Mật mã phi đối xứng AC độ dài bản rõ cố định chỉ mã hóa những bản rõ có độ dài (tính bằng số bộ tám) bằng một giá trị cố định AC.MsgLen.
- Mật mã phi đối xứng AC độ dài bản rõ bị giới hạn chỉ mã hóa những bản rõ có độ dài (tính bằng bộ tám) nhỏ hơn hoặc bằng một giá trị cố định AC.MaxMsgLen(PK). Ở đây độ dài cực đại của bản rõ có thể phụ thuộc vào khóa công khai của bản mã.
CHÚ THÍCH Ngoại trừ mật mã phi đối xứng độ dài bản rõ cố định và độ dài bản rõ bị giới hạn, phép mã hóa bản rõ nói chung không che giấu được độ dài bản rõ. Bởi vậy khi áp dụng mật mã phi đối xứng, cần thiết phải đảm bảo, có thể bằng cách sử dụng lược đồ đệm bản rõ, để không một thông tin nhạy cảm nào được mã hóa ở dạng ẩn có độ dài bằng độ dài bản rõ.
7.2. Sử dụng nhãn
Nhãn là xâu bộ tám mà giá trị của nó được sử dụng bởi các thuật toán mã hóa và giải mã. Nhãn có thể chứa dữ liệu công khai được che giấu khỏi ngữ cảnh và không cần thiết được mã hóa, nhưng nó lại phải liên quan đến bản mã.
Nhãn là xâu bộ tám có nhiều ý nghĩa đối với các ứng dụng sử dụng mật mã phi đối xứng và độc lập với quá trình thực thi mật mã phi đối xứng.
Nhãn có thể tùy ý, có độ dài thay đổi, mặc dù với mật mã cụ thể có thể chọn giới hạn trên (rất lớn) cho độ dài của nó.
Dạng suy biến của mật mã phi đối xứng được định nghĩa như sau:
- Mật mã phi đối xứng với độ dài nhãn cố định là mật mã với các thuật toán mã hóa và giải mã chỉ chấp nhận nhãn có độ dài (tính bằng bộ tám) bằng một giá trị cố định AC.LabelLen.
CHÚ THÍCH 1 Khái niệm an toàn truyền thống chống lại tấn công chọn bản mã, được mở rộng trong phụ lục B.4, sao cho bằng trực giác, đối với mật mã phi đối xứng, thuật toán mã hóa cần gắn nhãn vào bản mã theo một kiểu phù hợp "không có khả năng uốn”.
CHÚ THÍCH 2 Ví dụ, có những giao thức trao đổi khóa, trong đó một phía, chẳng hạn A mã hóa khóa phiên bằng khóa công khai của phía thứ hai, chẳng hạn B. Để giao thức được an toàn, định danh của phía A (hoặc khóa công khai hoặc chứng thư số) phải “không có khả năng bị uốn“ đối với bản mã. Một cách để thực hiện điều này là, đơn giản chỉ cần gắn định danh vào bản rõ. Tuy vậy, điều này làm cho bản mã trở nên dài không cần thiết, vì thường thì A đã biết định danh của B theo ngữ cảnh cụ thể của giao thức. Việc thực thi tốt cơ chế dán nhãn sẽ mang lại cùng hiệu quả, mà không cần tăng kích thước bản mã.
7.3. Định dạng bản mã
Mật mã phi đối xứng được đề xuất trong phần này của ISO/IEC 18033 mô tả chính xác cách định dạng bản mã như một xâu bộ tám. Tuy vậy, việc thực thi có thể tiến hành độc lập với lưu trữ và/hoặc truyền bản bản mã trong định dạng đã lựa chọn để thay thế, nếu như điều đó là thuận tiện. Hơn nữa, quá trình mã hóa bản rõ và biến đổi bản mã thu được theo định dạng đã chọn, có thể suy biến thành một quá trình đơn tương đương về chức năng. Tương tự như thế quá trình biến đổi từ định dạng đã chọn và giải mã bản mã có thể suy biến thành một quá trình đơn, tương đương về chức năng. Như vậy, trong hệ thống cho trước, bản mã nhất thiết không được xuất hiện ở dạng đã quy định ở đây.
CHÚ THÍCH Bên cạnh việc tăng cường tính liên tác, việc quy định định dạng của bản mã là cần thiết để đưa ra các mệnh đề có ý nghĩa và lập luận cứ cho tính an toàn của mật mã phi đối xứng chống lại các tấn công chọn bản mã phù hợp.
7.4. Lựa chọn mật mã
Một số mật mã phi đối xứng cho phép một số dạng tùy chọn cụ thể ở dạng lược đồ để chuyển sang thuật toán mật mã, điều này cắt nghĩa vì sao biến tùy chọn mật mã bổ sung opt lại được cho phép trong giao diện trừu tượng cho mật mã phi đối xứng.
Một số mật mã phi đối xứng được trình bày ở đây, một cách tự nhiên có thể xem như không chứa bất kỳ tùy chọn mật mã, trong những trường hợp như thế mật mã được coi là không có tùy chọn.
Hệ thống có thể cung cấp giá trị “mặc định” của biến opt. Tuy vậy, vấn đề này nằm ngoài phạm vi của phần này.
CHÚ THÍCH Trong các mật mã phi đối xứng được mô tả trong phần này của ISO/IEC 18033, chỉ có mật mã dựa trên đường cong elliptic là sử dụng chế độ tùy chọn mật mã, chế độ này được sử dụng nhằm chỉ dẫn định dạng mong muốn để mã hóa các điểm trên đường cong elliptic.
7.5. Phương pháp vận hành mật mã phi đối xứng
Thông thường, thuật toán tạo khóa do một bên thực hiện, đó là chủ nhân của cặp khóa, hoặc là bên được tin cậy được chủ nhân ủy thác. Khóa công khai được tạo ra cho tất cả các bên, những người muốn gửi thông báo được mã hóa đến cho chủ nhân, nhưng khóa riêng thì không được tiết lộ cho bất kỳ bên nào trừ chủ nhân của nó. Về cơ chế và các giao thức tạo khóa công khai cho các bên khác nằm ngoài phạm vi của phần này. Về vấn đề này xem hướng dẫn tại ISO/IEC 11770.
Mỗi một mật mã phi đối xứng được trình bày ở phần này của ISO/IEC 18033 là thành phần của họ các mật mã phi đối xứng, ở đấy mật mã cụ thể được chọn từ họ mật mã bằng cách chọn giá trị cụ thể của các tham số hệ thống, các tham số này xác định họ các mật mã.
Đối với mỗi mật mã cụ thể được chọn từ họ mật mã, các giá trị cụ thể được chọn trước khi tạo khóa. Tùy vào các quy ước được sử dụng để mã hóa khóa công khai, một số lựa chọn của tham số hệ thống có thể được nhúng vào quá trình mã hóa khóa công khai. Những tham số hệ thống này sẽ được cố định suốt cả thời gian sống của khóa công khai.
CHÚ THÍCH Ví dụ, nếu mã phi đối xứng có thể được tham số hóa theo thuật ngữ của hàm băm mật mã, thì việc chọn hàm hash nên được cố định và nói chung tại một điểm nào đó trước khi tạo cặp khóa công khai/khóa riêng, và các thuật toán mã hóa, giải mã nên sử dụng để chọn hàm băm suốt thời gian sống của khóa công khai. Bỏ qua nguyên tắc này không chỉ làm chệch việc thực thi, mà còn làm mất ý nghĩa của việc phân tích tính an toàn của mật mã, và có thể trong một số trường hợp, đẩy việc thực thi vào những rủi ro nghiêm trọng.
7.6. Mật mã phi đối xứng được phép
Người dùng muốn khai thác mật mã phi đối xứng trong phần này của ISO/IEC 18033 sẽ chọn một trong số các mật mã sau đây:
- Mật mã kết hợp vạn năng, được chọn từ họ HC các mật mã lai ghép, được mô tả tại Điều 8.3;
- Mã phi đối xứng với độ dài bản mã giới hạn từ họ RSAES các mật mã, được mô tả tại Điều 11.4;
- Mã phi đối xứng với độ dài bản rõ bị giới hạn thuộc họ HIME(R) được mô tả tại Điều 12.3.
CHÚ THÍCH Vì HC, RSAES và HIME là họ mật mã được tham số hóa bởi các tham số hệ thống khác nhau, người dùng sẽ phải chọn các giá trị cụ thể của các tham số hệ thống từ tập các tham số hệ thống được phép, được xác định trong các Điều tương ứng, trong đó mỗi họ mật mã được mô tả.
8 . Mật mã lai ghép tổng quát
Khi thiết kế mật mã phi đối xứng hiệu quả, một cách tiếp cận hữu ích là thiết kế mật mã lai ghép, ở đó có thể sử dụng kỹ thuật mật mã phi đối xứng để mã hóa khóa bí mật, khóa bí mật này sau đó được sử dụng để mã thông báo, sử dụng kỹ thuật mật mã đối xứng. Điều này mô tả một dạng mật mã lai đặc biệt, được gọi là mật mã lai ghép tổng quát. Mật mã lai ghép tổng quát được xây dựng từ hai “khối kiến tạo" mức thấp hơn: cơ chế bọc khóa và cơ chế bọc dữ liệu. Điều 8.3 đặc tả chi tiết họ HC các mật mã lai ghép tổng quát.
8.1. Cơ chế bọc khóa
Cơ chế bọc khóa KEM bao gồm ba thuật toán:
- Thuật toán tạo khóa KEM.KeyGen(), với đầu ra là cặp khóa công khai/khóa riêng (PK,pk). Cấu trúc của PK và pk phụ thuộc vào lược đồ cụ thể.
- Thuật toán mã hóa KEM.Encrypt(PK,opt), nhận đầu vào là khóa công khai PK và tùy chọn mật mã opt, đầu ra là cặp khóa mật/bản mã (K, C0). K và C0 là các xâu bộ tám. Vai trò của opt ở đây cũng tương tự như trong mật mã phi đối xứng (xem Điều 7.4).
- Thuật toán giải mã KEM.Decrypt (pk,C0) với đầu vào là khóa riêng pk và bản mã C0, đầu ra là khóa bí mật K, K và C0 là các xâu bộ tám.
Thuật toán giải mã có thể thất bại trong một số bối cảnh nhất định.
Cơ chế bọc khóa cũng xác định một số nguyên dương KEM.KeyLen - độ dài khóa bí mật là đầu ra của KEM.Encrypt và KEM.Decrypt.
CHÚ THÍCH Cơ chế bọc khóa cần thỏa mãn tính đúng đắn, tương tự tính đúng đắn của mật mã phi đối xứng: với bất kỳ cặp khóa công khai/khóa riêng (PK,pk), bất kỳ đầu ra (K, C0) của thuật toán mã hóa với đầu vào (PK,opt), bản mã C0 có thể được giải mã nhờ pk để thu được K. Yêu cầu này có thể được giảm nhẹ, bởi vậy nói chung chỉ nó chỉ giữ một phần không đáng kể cặp khóa công khai/bí mật.
8.1.1. Tính chất phi tiền tố
Ngoài ra, cơ chế bọc khóa còn phải thỏa mãn tính chất sau đây. Tập hợp tất cả các đầu ra - các bản mã có thể - của thuật toán mã hóa là tập con của tập ứng cử viên các xâu bộ tám (có thể phụ thuộc vào khóa công khai), sao cho tập ứng cử viên này là phi tiền tố và các phần tử của tập này dễ dàng được nhận dạng (hoặc cho trước khóa công khai hoặc khóa riêng).
8.1.2. Các cơ chế bọc khóa được phép
Cơ chế bọc khóa được phép trong phần này của tiêu chuẩn ISO/IEC 18033 gồm:
- ECIES - KEM (được mô tả tại Điều 10.2),
- PSEC - KEM (được mô tả tại Điều 10.3),
- ACE - KEM (được mô tả tại Điều 10.4), và
- RSA - KEM (được mô tả tại Điều 11.5).
CHÚ THÍCH 1 Để thuận tiện, các mật mã lai ghép tổng quát tương ứng được xây dựng từ các cơ chế bọc khóa trên thông qua cấu trúc lai ghép tổng quát tại Điều 8.3 tương ứng được gọi là ECIES - HC, PSEC - HC, ACE - HC, và RSA - HC.
CHÚ THÍCH 2 Nói một cách đại thể, cơ chế bọc khóa làm việc tương tự như mật mã phi đối xứng, ngoại trừ một điều là thuật toán mã hóa không nhận đầu vào nào khác ngoài khóa công khai của người nhận: thay vì nhận đầu vào là thông báo và tạo ra bản mã, thuật toán mã hóa tạo ra cặp khóa bí mật/bản mã (K, C0), ở đây K là xâu bộ tám có độ dài xác định và C0 là mã hóa của K, như vậy thuật toán giải mã áp dụng vào C0 và đưa ra K.
CHÚ THÍCH 3 Luôn luôn có thể sử dụng mật mã phi đối xứng (với độ dài bản rõ cố định hay độ dài bản rõ bị giới hạn) để tạo ra xâu bộ tám ngẫu nhiên K và sau đó mã hóa nó bằng khóa công khai của người nhận (và tùy chọn nào đó để thu được C0). Tuy nhiên, cũng có thể thiết kế cơ chế bọc khóa theo cách khác hiệu quả hơn.
CHÚ THÍCH 4: Để xây dựng mật mã lai ghép tổng quát an toàn chống lại tấn công chọn bản mã phù hợp, tồn tại khái niệm an toàn tương ứng cho cơ chế bọc khóa. Điều này được thảo luận chi tiết tại Phụ lục B.5.
8.2. Các cơ chế bọc dữ liệu
Cơ chế bọc dữ liệu DEM xác định độ dài khóa DEM.KeyLen, và các thuật toán mã hóa và giải mã.
- Thuật toán mã hóa DEM.Encrypt(K,L,M) nhận đầu vào là khóa bí mật K, nhãn L và bản rõ M. Thuật toán cho đầu ra là bản mã C1. Ở đây K, L, M và C1 là các xâu bộ tám, trong đó L và M có thể có độ dài tùy ý, còn K có độ dài DEM.KeyLen.
Thuật toán mã hóa có thể bị thất bại, nếu độ dài L hoặc M vượt qua giới hạn (rất lớn) được xác định bởi quá trình thực thi.
- Thuật toán giải mã DEM.Decrypt(K,L,C1) nhận đầu vào là khóa bí mật K, nhãn L và bản mã C1 cho đầu ra là bản rõ M.
Thuật toán giải mã có thể thất bại trong một số bối cảnh nhất định.
CHÚ THÍCH Các thuật toán mã hóa và giải mã nên là thuật toán tất định, thỏa mãn yêu cầu sau đây về tính đúng đắn: với mọi khóa bí mật, tất cả L vá tất cả bản rõ, đều có độ dài L và M không vượt quá giới hạn được xác định bởi thực thi,
DEM.Decrypt(K,L,DEM.Encrypt(K,L,M)) = M.
8.2.1. Các dạng cơ chế bọc dữ liệu suy biến
Có hai dạng cơ chế bọc dữ liệu suy biến được xác định như sau:
- Cơ chế bọc dữ liệu với độ dài nhãn cố định là cơ chế mà thuật toán mã hóa và giải mã chỉ chấp nhận nhãn có độ dài bằng giá trị cố định DEM.LabelLen.
- Cơ chế bọc dữ liệu với độ dài bản rõ cố định là cơ chế mã thuật toán mã hóa chỉ chấp nhận các bản rõ có độ dài bằng giá trị cố định DEM.MsgLen.
8.2.2. Cơ chế bọc dữ liệu được phép
Cơ chế bọc dữ liệu trong phần này của tiêu chuẩn ISO/IEC 18033 được mô tả tại Điều 9.
CHÚ THÍCH 1 Nói đại thể, cơ chế bọc dữ liệu cung cấp “phong bì số", bảo vệ cả tính bí mật lẫn tính toàn vẹn của dữ liệu sử dụng kỹ thuật mật mã đối xứng. Nó đồng thời gắn dữ liệu vào nhãn công khai.
CHÚ THÍCH 2 Để xây dựng mã lai ghép tổng quát, chống được tấn công chọn bản mã, tồn tại khái niệm tương ứng về an toàn cho cơ chế bọc dữ liệu. Điều này được xem xét chi tiết tại Phụ lục B.6.
8.3. HC
8.3.1. Các tham số hệ thống
HC là họ mật mã phi đối xứng được tham số hóa như sau:
- KEM: cơ chế bọc khóa được mô tả tại Điều 8.1;
- DEM: cơ chế bọc khóa được mô tả tại Điều 8.2.
Mọi sự kết hợp giữa KEM và DEM đều có thể sử dụng, nếu đảm bảo điều kiện KEM.KeyLen = DEM.KeyLen.
CHÚ THÍCH 1 Nếu DEM là cơ chế bọc dữ liệu với độ dài nhãn cố định, trong đó độ dài nhãn bị hạn chế bởi DEM.LabelLen, thì HC là mã đối xứng với độ dài nhãn cố định và HC.LabelLen = DEM.KeyLen.
CHÚ THÍCH 2 Nếu DEM là cơ chế bọc dữ liệu với độ dài bản rõ cố định, trong đó bản rõ có độ dài hạn chế bởi DEM.MsgLen, thì HC là mã đối xứng với độ dài bản rõ cố định và HC.MsgLen = DEM.MsgLen.
CHÚ THÍCH 3 Với tất cả sự lựa chọn được phép của KEM, giá trị của KEM.KeyLen là tham số hệ thống có thể được chọn bằng DEM.KeyLen. Như vậy mọi sự kết hợp có thể của KEM và DEM có thể được thực hiện bằng cách chọn thích hợp các tham số hệ thống.
8.3.2. Tạo khóa
Thuật toán tạo khóa, khóa công khai và khóa riêng cho HC cũng như cho KEM; Tùy chọn mật mã của HC cũng như của KEM.
Giả sử (PK, pk) là cặp khóa công khai/khóa riêng.
8.3.3. Mã hóa
Thuật toán mã hóa HC.Encrypt nhận đầu vào là khóa công khai PK, nhãn L, bản rõ M và tùy chọn mật mã opt. Thuật toán này chạy như sau:
a) Tính (K,C0) = KEM.Encrypt(PK,opt).
b) Tính C1 = DEM.Encrypt(K,L,M).
c) Tạo C = C0 || C1.
d) Đưa ra C.
8.3.4. Giải mã
Thuật toán giải mã HC.Decrypt nhận đầu vào là khóa riêng pk, nhãn L và bản mã C. Thuật toán chạy như sau:
a) Sử dụng tính chất phi tiền tố của bản mã liên kết với KEM (xem Điều 8.1.1), tạo cú pháp C, C = C0||C1, ở đây C0 và C1 là các xâu bộ tám sao cho C0 là phần tử của tập hợp ứng cử viên của các bản mã có thể liên kết với KEM. Bước này sẽ thất bại nếu C không được tạo cú pháp.
b) Tính K = KEM.Decrypt(pk, C0).
c) Tính M = DEM.Decrypt (K, L, C1).
d) Đưa ra M.
CHÚ THÍCH độ an toàn của HC được xem xét tại phụ lục B.7. Tại đây lưu ý rằng chừng nào KEM và DEM thỏa mãn các tính chất an toàn tương ứng, thì HC sẽ là an toàn đối với tấn công chọn bản mã thích hợp.
9. Thiết kết các cơ chế bọc dữ liệu
Điều khoản này đưa ra các cơ chế bọc dữ liệu, gồm:
- DEM1, được mô tả trong Điều 9.1,
- DEM2, được mô tả trong Điều 9.2, và
- DEM3, được mô tả trong Điều 9.3.
9.1. DEM1
9.1.1. Các tham số hệ thống
DEM1 là họ các cơ chế bọc dữ liệu, được tham số hóa bằng các tham số hệ thống sau:
- SC: mật mã đối xứng, được mô tả tại Điều 6.5;
- MA: thuật toán MAC được mô tả trong Điều 6.3.
Giá trị của DEM1.KeyLen được xác định như sau: DEM1.KeyLen = SC.KeyLen + MA. KeyLen.
9.1.2. Mã hóa
Thuật toán DEM1.Encrypt nhận đầu vào là khóa bí mật K, nhãn L, và bản rõ M. Thuật toán chạy như sau:
a) Tạo cú pháp K, K = ![]() , ở đây k và k' là các xâu bộ tám sao cho |k| = SC.KeyLen và |k'| = MA.KeyLen.
, ở đây k và k' là các xâu bộ tám sao cho |k| = SC.KeyLen và |k'| = MA.KeyLen.
b) Tính c = SC.Encrypt(k,M).
c) Giả sử T = ![]()
d) Tính MAC = MA.eval(k',T).
e) Thiết lập C1 = c || MAC.
f) Đưa ra C1.
9.1.3. Giải mã
Thuật toán DEM1.Decrypt nhận đầu vào là khóa bí mật K, nhãn L, và bản mã C1. Thuật toán chạy như sau:
a) Tạo cú pháp K,K = ![]() ở đấy k và k' là các xâu bộ tám với |k| = SC.KeyLen và |k'| = MA.KeyLen.
ở đấy k và k' là các xâu bộ tám với |k| = SC.KeyLen và |k'| = MA.KeyLen.
b) Nếu |C1| < MA.MACLen thì thất bại.
c) Tạo cú pháp C1 : C1 = ![]() , ở đây c và MAC là các xâu bộ tám với |MAC| = MA.MACLen.
, ở đây c và MAC là các xâu bộ tám với |MAC| = MA.MACLen.
d) Giả sử T = ![]()
e) Tính MAC' = MA.eval(k',T).
f) Nếu MAC ¹ MAC' thì thất bại.
g) Tính M = SC.Decrypt(k,c).
h) Đưa ra M.
CHÚ THÍCH Việc xem xét chi tiết tính an toàn của cấu trúc này được đưa ra trong Phụ lục B.6.1. Ở đây chỉ lưu ý là các SA và MA cơ sở được cung cấp thỏa mãn các yêu cầu tương ứng, sau đó là cả DEM1 cũng thỏa mãn các yêu cầu này.
9.2. DEM2
9.2.1. Các tham số hệ thống
DEM2 là họ các cơ chế bọc dữ liệu với độ dài nhãn cố định, được tham số hóa bằng các tham số hệ thống sau đây:
- SC: mã đối xứng được mô tả tại Điều 6.5;
- MA: thuật toán MAC, được mô tả tại Điều 6.3;
- LabelLen: số nguyên không âm.
Giá trị DEM2.LabelLen được xác định là bằng giá trị của tham số hệ thống LabelLen.
Giá trị DEM2.KeyLen được xác định bằng: DEM2.KeyLen = SC.KeyLen + MA.KeyLen.
9.2.2. Mã hóa
Thuật toán DEM2.Encrypt nhận đầu vào là khóa bí mật K, nhãn L độ dài LabelLen, bản rõ M. Thuật toán chạy như sau:
a) Tạo cú pháp K, K = ![]() ở đấy k và k' là các xâu bộ tám sao cho |k| = SC.KeyLen và |k'| = MA.KeyLen.
ở đấy k và k' là các xâu bộ tám sao cho |k| = SC.KeyLen và |k'| = MA.KeyLen.
b) Tính c = SC.Encrypt(k,M).
c) Đặt T = ![]() .
.
d) Tính MAC = MA.eval (k',T).
e) Thiết lập C1= c || MAC.
f) Đưa ra C1.
9.2.3. Giải mã
Thuật toán DEM2.Decrypt nhận đầu vào là khóa bí mật K, nhãn L độ dài LabelLen và bản mã C1. Thuật toán chạy như sau:
a) Tạo cú pháp K, K = ![]() ở đấy k và k’ là các xâu bộ tám sao cho |k| = SC.KeyLen và |k'| = MA. KeyLen.
ở đấy k và k’ là các xâu bộ tám sao cho |k| = SC.KeyLen và |k'| = MA. KeyLen.
b) Nếu |C1| < MA.MACLen thì thất bại.
c) Tạo cú pháp C1,C1 = ![]() , ở đây c và MAC là các xâu bộ tám sao cho |MAC| = MA.MACLen.
, ở đây c và MAC là các xâu bộ tám sao cho |MAC| = MA.MACLen.
d) Giả sử T = c || L.
e) Tính MAC' = MA.eval (k',T).
f) Nếu MAC' ¹ MAC thì thất bại.
g) Tính M = SC.Decrypt(k,c).
h) Đưa ra M.
CHÚ THÍCH 1 Việc xem xét chi tiết tính an toàn của thiết kế trên được trình bày trong Phụ lục B.6.1. Ở đây chỉ lưu ý là các SC và MA thỏa mãn các yêu cầu an toàn tương ứng, khi đó DEM2 cũng thỏa mãn các yêu cầu này.
CHÚ THÍCH 2 DEM2 được cung cấp chủ yếu để so sánh với các tiêu chuẩn khác.
9.3. DEM3
9.3.1. Các tham số hệ thống
DEM3 là họ các cơ chế bọc dữ liệu với độ dài bản rõ cố định, được tham số hóa bởi các tham số hệ thống sau đây:
- MA: thuật toán MAC được mô tả ở Điều 6.3;
- MsgLen: số nguyên dương.
Giá trị của DEM3.MsgLen được định nghĩa bằng giá trị của tham số hệ thống MsgLen.
Giá trị của DEM3.KeyLen được xác định bằng,
DEM3.KeyLen = MsgLen + MA.KeyLen.
9.3.2. Mã hóa
Thuật toán DEM3.Encrypt nhận đầu vào là khóa bí mật K, nhãn L, bản rõ M với độ dài MsgLen. Thuật toán chạy như sau:
a) Tạo cú pháp K, K = ![]() ở đấy k và k’ là các xâu bộ tám (octet) với |k| = MsgLen và |k'| = MA.KeyLen.
ở đấy k và k’ là các xâu bộ tám (octet) với |k| = MsgLen và |k'| = MA.KeyLen.
b) Tính c = k Å M.
c) Giả sử T = ![]() .
.
d) Tính MAC = MA.eval (k',T).
e) Đặt C1 = c || MAC.
f) Đưa ra C1.
9.3.3. Giải mã
Thuật toán DEM3.Decrypt nhận đầu vào là khóa bí mật K, nhãn L và bản mã C1. Thuật toán chạy như sau:
a) Tạo cú pháp cho K, K = ![]() ở đấy k và k’ là các xâu bộ tám với |k| = MsgLen và |k'| = MA.KeyLen.
ở đấy k và k’ là các xâu bộ tám với |k| = MsgLen và |k'| = MA.KeyLen.
b) Nếu C1 ¹ MsgLen + MA.MACLen thì thất bại.
c) Tạo cú pháp C1:C1 = ![]() , ở đây c và MAC là các xâu bộ tám với |c| = Msglen và |MAC| = MA.MACLen.
, ở đây c và MAC là các xâu bộ tám với |c| = Msglen và |MAC| = MA.MACLen.
d) Đặt T = ![]() .
.
e) Tính MAC’ = MA.eval (k',T).
f) Nếu MAC ¹ MAC' thì thất bại.
g) Tính M = k Å c.
h) Đưa ra M
CHÚ THÍCH 1 Việc xem xét chi tiết tính an toàn của thiết kế này được trình bày ở Phụ lục B.6.1. Cần lưu ý ở đây là nếu SC và MA thỏa mãn các yêu cầu an toàn tương ứng thì DEM3 cũng thỏa mãn các yêu cầu đó.
CHÚ THÍCH 2 DEM3 được cung cấp chủ yếu để so sánh với các tiêu chuẩn khác.
10. Cơ chế bọc khóa dựa vào EIGamal
Điều này mô tả một số cơ chế bọc khóa dựa trên bài toán logarit rời rạc:
- ECIES-KEM được mô tả trong Điều 10.2;
- PSEC-KEM được mô tả trong Điều 10.3;
- ACE-KEM được mô tả trong Điều 10.4.
CHÚ THÍCH Tất cả các lược đồ trên đều là những biến thể của lược đồ mật mã góc EIGamal [18].
10.1. Các nhóm cụ thể
Mật mã EIGamal dựa trên các phép toán số học trên nhóm hữu hạn. Để mô tả cơ chế bọc khóa dựa trên mật mã EIGamal, khái niệm nhóm được mô tả như một kiểu dữ liệu trừu tượng. Việc mô tả và phân tích các lược đồ dựa vào giao diện trừu tượng này, tuy nhiên trong phần này của tiêu chuẩn ISO/IEC 18033, chỉ cho phép sử dụng một số dạng nhóm nhất định bằng cách cụ thể hóa kiểu dữ liệu trừu tượng này.
Để tiện, khái niệm phép cộng luôn được sử dụng cho nhóm. Đồng thời các phần tử của nhóm sẽ được viết bằng chữ cái thường, đậm nét và 0 ký hiệu phần tử đồng nhất của nhóm.
Nhóm cụ thể G là bộ ![]()
- ![]() là nhóm Abel hữu hạn. Chú ý rằng nhóm không nhất thiết là tuần hoàn.
là nhóm Abel hữu hạn. Chú ý rằng nhóm không nhất thiết là tuần hoàn.
- ![]() là nhóm con tuần hoàn của
là nhóm con tuần hoàn của ![]()
- ![]() là phần tử sinh của
là phần tử sinh của ![]()
- μ là bậc của ![]() , và v là chỉ số của
, và v là chỉ số của ![]() trong
trong ![]() , nghĩa là v = |
, nghĩa là v = |![]() |/μ
|/μ
Ở đây đòi hỏi μ phải là số nguyên tố. Trong một số lược đồ mật mã, đòi hỏi thêm điều kiện gcd(μ,v) = 1.
- ε(a,fmt) là hàm “mã hóa" (encoding function), ánh xạ phần tử nhóm ![]() vào xâu bộ tám; biến thứ hai fmt là bộ định dạng, được sử dụng để chọn một trong số lượng nhỏ các định dạng có thể để mã hóa phần tử của nhóm. Các giá trị được phép của biến fmt phụ thuộc vào nhóm.
vào xâu bộ tám; biến thứ hai fmt là bộ định dạng, được sử dụng để chọn một trong số lượng nhỏ các định dạng có thể để mã hóa phần tử của nhóm. Các giá trị được phép của biến fmt phụ thuộc vào nhóm.
Các yêu cầu sau phải được thỏa mãn:
- Tập tất cả các đầu ra ε là tập phi tiền tố.
- Phần tử trung hòa được mã hóa (encoding) duy nhất, bởi vậy với tất cả các biến định dạng fmt, fmt’ ta có: ε(0,fmt) = ε(0,fmt’).
- Trừ phần tử trung hòa, hàm mã hóa là ánh xạ một-một, do đó với tất cả a và a’ ![]() và tất cả các biến định dạng fmt,fmt', nếu (a,fmt) ¹ (a',fmt') và nếu a ¹ 0 hoặc a’ ¹ 0, thì ε(a,fmt) ¹ ε(a',fmt').
và tất cả các biến định dạng fmt,fmt', nếu (a,fmt) ¹ (a',fmt') và nếu a ¹ 0 hoặc a’ ¹ 0, thì ε(a,fmt) ¹ ε(a',fmt').
Xâu bộ tám x được gọi là mã hợp lệ (valid encoding) của phần tử nhóm ![]() , nếu x = ε(a,fmt) với một biến định dạng fmt nào đó.
, nếu x = ε(a,fmt) với một biến định dạng fmt nào đó.
- D(x) là hàm sao cho nó sẽ trả về nếu x không phải là mã hợp lệ của phần tử thuộc ![]() , ngược lại, hàm hoàn lại phần tử nhóm duy nhất
, ngược lại, hàm hoàn lại phần tử nhóm duy nhất ![]() , sao cho ε(a,fmt) = x với một biến định dạng fmt nào đó.
, sao cho ε(a,fmt) = x với một biến định dạng fmt nào đó.
- ε'(a) là hàm "mã từng phần”, ánh xạ mỗi phần tử nhóm ![]() , vào xâu bộ tám.
, vào xâu bộ tám.
Điều này đòi hỏi tập hợp tất cả đầu ra của ε' là phi tiền tố.
Xâu bộ tám x được gọi là mã từng phần hợp lệ (valid partial encoding) của phần tử nhóm a nếu x = ε'(a).
- D'(x) là hàm sao cho hoặc là thất bại nếu x không phải là mã cụ thể của phần tử thuộc ![]() ; ngược lại, nó sẽ trả về một tập hợp chứa tất cả các phần tử nhóm
; ngược lại, nó sẽ trả về một tập hợp chứa tất cả các phần tử nhóm ![]() , sao cho ε'(a) = x. Giả thiết kích thước của tập hợp này bị giới hạn bởi một hằng số nhỏ.
, sao cho ε'(a) = x. Giả thiết kích thước của tập hợp này bị giới hạn bởi một hằng số nhỏ.
Giả thiết có thể thực hiện hiệu quả các phép toán số học trong ![]() . Đồng thời, tất cả các thuật toán trên đây đều được thực thi hiệu quả. Hàm D' sẽ không được sử dụng bởi bất kỳ lược đồ nào, nhưng sự tồn tại của hàm này là cần cho việc phân tích tính an toàn các lược đồ đó.
. Đồng thời, tất cả các thuật toán trên đây đều được thực thi hiệu quả. Hàm D' sẽ không được sử dụng bởi bất kỳ lược đồ nào, nhưng sự tồn tại của hàm này là cần cho việc phân tích tính an toàn các lược đồ đó.
Giả sử có thể kiểm tra hiệu quả, liệu một phần tử của ![]() có nằm trong nhóm con
có nằm trong nhóm con ![]() hay không. Lưu ý rằng nếu tất cả các phần tử của
hay không. Lưu ý rằng nếu tất cả các phần tử của ![]() , có bậc μ nằm trong
, có bậc μ nằm trong ![]() , thì có thể kiểm tra
, thì có thể kiểm tra ![]() bằng cách kiểm tra điều kiện μ.a = 0. Bởi vậy phép kiểm tra này có thể áp dụng được nếu bản thân
bằng cách kiểm tra điều kiện μ.a = 0. Bởi vậy phép kiểm tra này có thể áp dụng được nếu bản thân ![]() là nhóm tuần hoàn và gcd(μ,v) = 1. Với các nhóm cụ thể, có thể có các phép kiểm tra hiệu quả hơn về việc phần tử cho trước có thuộc nhóm con hay không.
là nhóm tuần hoàn và gcd(μ,v) = 1. Với các nhóm cụ thể, có thể có các phép kiểm tra hiệu quả hơn về việc phần tử cho trước có thuộc nhóm con hay không.
Tập hợp {ε(a1,fmt1),....,ε(am,fmtm)} các mã hợp lệ được gọi là tập bền vững, nếu mã (encodings) của các phần tử nhóm không phải là phần tử trung hòa sử dụng cùng một biến định dạng fmt; bởi vậy với mọi 1 ≤ i, j ≤ m, nếu ai ≠ 0, aj ≠ 0 thì fmti = fmtj. Với những giả thiết như trên có thể kiểm tra một cách hiệu quả một tập hợp các mã hợp lệ cho trước có bền vững hay không.
CHÚ THÍCH Các ứng dụng mật mã khác nhau sẽ đưa ra các giả thiết khác nhau về tính khó giải của nhóm. Những giả thiết này được xem xét tại Phụ lục B.8.
10.1.1. Các nhóm cụ thể được phép
Phần này của ISO/IEC 18033 chỉ cho phép hai họ nhóm cụ thể sau đây, được mô tả tại các Điều 10.1.2 va 10.1.3.
10.1.2. Nhóm con của các trường hữu hạn được cho dưới dạng tường minh
Giả sử F là trường hữu hạn dạng tường minh, được định nghĩa tại Điều 5.3 và F* là nhóm nhân các đơn vị của F. Giả sử ![]() là ký hiệu của F* và
là ký hiệu của F* và ![]() là nhóm con của F* có bậc nguyên tố, g là phần tử sinh của
là nhóm con của F* có bậc nguyên tố, g là phần tử sinh của ![]() . Đặt μ = |
. Đặt μ = |![]() | và v = (|F| - 1) /μ.
| và v = (|F| - 1) /μ.
Vì ![]() là nhóm tuần hoàn, suy ra
là nhóm tuần hoàn, suy ra ![]() chứa tất cả các phần tử của
chứa tất cả các phần tử của ![]() có bậc chia hết μ, thậm chí khi gcd (μ, v) ≠ 1. Như vậy, luôn luôn có thể kiểm tra phần tử
có bậc chia hết μ, thậm chí khi gcd (μ, v) ≠ 1. Như vậy, luôn luôn có thể kiểm tra phần tử ![]() có thuộc
có thuộc ![]() hay không bằng cách kiểm tra hệ thức μ.a = 0. Tuy nhiên, còn có thể có những phép kiểm tra hiệu quả hơn, ví dụ nếu F là trường hữu hạn nguyên tố và v = 2, thì phép kiểm tra này có thể thực hiện bằng cách tính ký hiệu Jacobi.
hay không bằng cách kiểm tra hệ thức μ.a = 0. Tuy nhiên, còn có thể có những phép kiểm tra hiệu quả hơn, ví dụ nếu F là trường hữu hạn nguyên tố và v = 2, thì phép kiểm tra này có thể thực hiện bằng cách tính ký hiệu Jacobi.
Ánh xạ mã hóa ε(encoding map) được thực thi bằng cách sử dụng hàm FE2OSPF, bởi vậy tất cả các phần tử nhóm được mã hóa dưới dạng các xâu bộ tám có độ dài ![]() .Chỉ cho phép một định dạng. Ánh xạ
.Chỉ cho phép một định dạng. Ánh xạ ![]() được thực thi bằng cách sử dụng OS2FEPF và thất bại nếu OS2FEPF thất bại hoặc đưa ra 0F. Hàm ε' cũng giống như ε và
được thực thi bằng cách sử dụng OS2FEPF và thất bại nếu OS2FEPF thất bại hoặc đưa ra 0F. Hàm ε' cũng giống như ε và ![]() cũng giống như
cũng giống như ![]()
10.1.3. Nhóm con của đường cong Elliptic
Giả sử E là đường cong elliptic trên trường hữu hạn dạng tường minh F, được mô tả tại Điều 5.4. Ký hiệu ![]() là nhóm các điểm trên E,
là nhóm các điểm trên E, ![]() là nhóm con bậc nguyên tố của
là nhóm con bậc nguyên tố của ![]() là phần tử sinh của
là phần tử sinh của ![]() ; giả sử μ là bậc của
; giả sử μ là bậc của ![]() , v là chỉ số của nó trong
, v là chỉ số của nó trong ![]() .
.
Ta thấy, nói chung ![]() không phải là nhóm tuần hoàn. Nếu gcd (μ,v) = 1 thì có thể kiểm tra phần tử
không phải là nhóm tuần hoàn. Nếu gcd (μ,v) = 1 thì có thể kiểm tra phần tử ![]() có nằm trong
có nằm trong ![]() hay không, bằng cách kiểm tra hệ thức μ.a = 0. Nếu gcd(μ, v) ≠ 1 khi đó yêu cầu phải có nhiều thông tin hơn về cấu trúc nhóm của E để xây dựng nên phép kiểm tra hiệu quả về việc phần tử thuộc
hay không, bằng cách kiểm tra hệ thức μ.a = 0. Nếu gcd(μ, v) ≠ 1 khi đó yêu cầu phải có nhiều thông tin hơn về cấu trúc nhóm của E để xây dựng nên phép kiểm tra hiệu quả về việc phần tử thuộc ![]() có nằm trong
có nằm trong ![]() hay không.
hay không.
Các ánh xạ mã hóa/ giải mã ε và …… được thực thi bằng cách sử dụng các hàm EC2OSPE và OS2ECPE. Như vậy mã hóa của điểm là xâu bộ tám có độ dài hoặc bằng 1 hoặc bằng ![]() , hoặc
, hoặc ![]() . Tập tất cả các biến định dạng được phép có thể được chọn là tập con không rỗng bất kỳ của tập {không nén, nén, lai ghép}. Như vậy nhóm cụ thể được xác định nhờ sử dụng đường cong elliptic, có thể, nhưng không nhất thiết, cho phép sử dụng các định dạng đa mã hóa.
. Tập tất cả các biến định dạng được phép có thể được chọn là tập con không rỗng bất kỳ của tập {không nén, nén, lai ghép}. Như vậy nhóm cụ thể được xác định nhờ sử dụng đường cong elliptic, có thể, nhưng không nhất thiết, cho phép sử dụng các định dạng đa mã hóa.
Ánh xạ mã hóa cụ thể ε' được xác định như sau: Cho điểm P trên E, nếu P = ![]() thì đầu ra là FE2OSPF(0F) và nếu P = (x,y) ≠
thì đầu ra là FE2OSPF(0F) và nếu P = (x,y) ≠ ![]() ,ở đấy x,y Î F, thì đầu ra là FE2OSPF(x). Như vậy đầu ra của ε' là xâu bộ tám độ dài
,ở đấy x,y Î F, thì đầu ra là FE2OSPF(x). Như vậy đầu ra của ε' là xâu bộ tám độ dài ![]()
10.2. ECIES-KEM
Điều này mô tả cơ chế bọc khóa ECIES - KEM.
CHÚ THÍCH ECIES - KEM dựa trên công trình của Adballa, Bellare và Rogaway [1,2].
10.2.1. Các tham số hệ thống
ECIES - KEM là họ các cơ chế bọc khóa, được tham số hóa bởi các tham số hệ thống sau đây:
- G: nhóm cụ thể
![]()
như mô tả trong Điều 10.1;
- KDF: Hàm dẫn xuất khóa, như đã mô tả tại Điều 6.2;
- CofactorMode: một trong hai giá trị 0 hoặc 1.
- OldCofactorMode: một trong hai giá trị 0 hoặc 1.
- CheckMode:một trong hai giá trị 0 hoặc 1.
- SingleHashMode: một trong hai giá trị 0 hoặc 1.
- KeyLen: số nguyên.
Bất kỳ một tổ hợp nào các tham số hệ thống đều cho phép, trừ các hạn chế sau:
- Nhiều nhất một trong các tham số CofactorMode, OldCofactorMode và CheckMode có thể là 1.
- Nếu v > 1 và CheckMode = 0, khi đó phải có gcd(μ, v) = 1.
Giá trị ECIES - KEM.KeyLen được định nghĩa bằng giá trị của tham số hệ thống Keylen.
CHÚ THÍCH Các giá trị của CofactorMode và CheckMode chỉ được sử dụng bởi thuật toán giải mã.
10.2.2. Tạo khóa
Thuật toán tạo khóa ECIES - KEM.KeyGen không nhận đầu vào, và chạy như sau:
a) Tạo số ngẫu nhiên x Î [1 ...μ).
b) Tính h = x.g.
c) Đưa ra khóa công khai đầu ra:
- h: phần tử khác không của ![]()
d) Đưa ra khóa riêng đầu ra:
- x: số nguyên thuộc tập hợp [1,...,μ).
10.2.3. Mã hóa
Thuật toán ECIES - KEM.Encrypt nhận đầu vào là khóa công khai, gồm phần tử ![]() cùng với tùy chọn mật mã fmt xác định định dạng dùng để mã hóa các phần tử của nhóm. Thuật toán được thực hiện như sau:
cùng với tùy chọn mật mã fmt xác định định dạng dùng để mã hóa các phần tử của nhóm. Thuật toán được thực hiện như sau:
a) Tạo số ngẫu nhiên r Î [1,...,μ).
b) Nếu OldCofactorMode = 1 thì đặt r' = r.vmod μ, ngược lại thì đặt r’ = r.
c) Tính ![]() = r.g và
= r.g và ![]() = r'.h
= r'.h
d) Đặt C0 = ε{![]() ,fmt).
,fmt).
e) Nếu SingleHashMode = 1 thì Z là xâu bộ tám gồm toàn phần tử 0; ngược lại đặt Z = C0.
f) Đặt PEH = ε'(![]() ).
).
g) Đặt K = KDF(Z || PEH,KeyLen).
h) Đưa ra bản mã C0 và khóa bí mật K.
10.2.4. Giải mã
Thuật toán giải mã ECIES - KEM.Decrypt nhận đầu vào là khóa bí mật K, gồm phần tử r Î [1 ...μ), và bản mã C0. Thuật toán thực hiện như sau:
a) Đặt ![]() ; bước này sẽ thất bại nếu C0 không phải là mã hợp lệ của phần tử thuộc
; bước này sẽ thất bại nếu C0 không phải là mã hợp lệ của phần tử thuộc ![]()
b) Nếu CheckMode = 1, Kiểm tra ![]() nếu không thỏa mãn thì thất bại.
nếu không thỏa mãn thì thất bại.
c) Nếu CofactorMode = 1 hoặc OldCofactorMode = 1, đặt ![]() , nếu ngược lại thì đặt
, nếu ngược lại thì đặt ![]()
d) Nếu Cofactor = 1, khi đó ![]() = v-1xmod μ, ngược lại đặt
= v-1xmod μ, ngược lại đặt ![]() = x.
= x.
e) Tính ![]() =
= ![]() .
.
f) Nếu ![]() = 0 thì thất bại.
= 0 thì thất bại.
g) Nếu SingleHashMode = 1 thì cho Z là xâu bộ tám rỗng, ngược lại giả sử Z = C0.
h) Đặt PEH = ε’(![]() ).
).
i) Đặt K = KDF(Z || PEH, KeyLen).
j) Đưa ra là khóa bí mật K
CHÚ THÍCH Sử dụng CofactorMode = 1 hoặc OldCofactorMode = 1 có thể mang lại lợi ích đáng kể trong thực thi, nếu v thật sự nhỏ. Ưu điểm của việc sử dụng CofactorMode = 1 là ở chỗ hành vi của thuật toán mã hóa không bị ảnh hưởng bởi giá trị của CofactorMode.
CHÚ THÍCH 2 Khi sử dụng CofactorMode = 1, việc thực thi có thể đơn giản là tính trước và lưu giá trị ![]() thay vì tính x.
thay vì tính x.
CHÚ THÍCH 3 Khi sử dụng SingleHashMode = 1, thậm chí nếu G hỗ trợ định dạng đa mã, giá trị của fmt được sử dụng trong khi mã hóa không ảnh hưởng lên bất kỳ tính toán nào, ngoại trừ định dạng cho bản mã cuối cùng. Như vậy, nếu bản mã cho trước C0 là kết quả mã hóa của phần tử nhóm ![]() , thì một bản mã khác C'0 đồng thời cũng là kết quả mã hóa (encoding) của
, thì một bản mã khác C'0 đồng thời cũng là kết quả mã hóa (encoding) của ![]() cũng sẽ được giải mã bằng cách như với C0.
cũng sẽ được giải mã bằng cách như với C0.
CHÚ THÍCH 4: Việc xem xét tính an toàn của lược đồ này được trình bày trong Phụ lục B.9.
10.3. PSEC-KEM
Điều này mô tả cơ chế bọc khóa PSEC - KEM.
CHÚ THÍCH PSEC - KEM dựa trên công trình của Fujisaki và Okamoto [26].
10.3.1. Các tham số hệ thống
PSEC - KEM là họ các cơ chế bọc khóa, được tham số hóa bởi các tham số hệ thống sau đây:
- G: nhóm cụ thể
![]()
được mô tả ở Điều 10.1;
- KDF: Hàm xuất khóa được mô tả ở Điều 6.2;
- SeedLen: số nguyên dương;
- KeyLen: số nguyên dương.
10.3.2. Tạo khóa
Thuật toán tạo PSEC - KEM.KeyGen không có đầu vào, thực hiện như sau:
a) Tạo số ngẫu nhiên x Î [0...μ).
b) Tính h = x.g.
c) Đưa ra khóa công khai:
- h: phần tử của ![]()
d) Đưa ra khóa bí mật:
x: số nguyên thuộc tập hợp [0,...,μ).
10.3.3. Mã hóa
Giả sử I0 = I2OSP(0,4) và I1 = I2OSP(1,4).
Thuật toán mã hóa PSEC - KEM.Encrypt nhận đầu vào là khóa công khai, gồm phần tử h Î ![]() , cùng với tùy chọn mật mã fmt, đưa ra định dạng dùng để mã hóa phần tử của nhóm. Thuật toán được thực hiện như sau:
, cùng với tùy chọn mật mã fmt, đưa ra định dạng dùng để mã hóa phần tử của nhóm. Thuật toán được thực hiện như sau:
a) Tạo xâu bộ tám ngẫu nhiên seed độ dài SeedLen.
b) Tính ![]() ,
,
là xâu bộ tám độ dài ![]()
c) Tạo cú pháp cho t, t = u || K, ở đây u và K là các xâu bộ tám sao cho ![]() và |K| = KeyLen.
và |K| = KeyLen.
d) Tính r = OS2IP(u) mod μ.
e) Đặt ![]() = r.g,
= r.g, ![]() = r.h.
= r.h.
f) Đặt EG = ε(![]() ,fmt) và PEH = ε'(
,fmt) và PEH = ε'(![]() ).
).
g) Đặt SeedMask = KDF(I1 || EG || PEH,SeedLen).
h) Đặt MaskedSeed = seedÅSeedMask.
i) Đặt C0 = EG || MaskedSeed.
j) Đưa ra là bản mã C0 và khóa bí mật K.
10.3.4. Giải mã
Giả sử I0 = I2OSP(0,4) và I1 = I2OSP(1,4).
Thuật toán giải mã PSEC - KEM.Decrypt nhận đầu vào là khóa bí mật K, gồm phần tử x Î [0 ... μ) và bản mã C0. Thuật toán thực hiện như sau:
a) Tạo cú pháp C0, C0 = EG || MaskedSeed, EG và MaskedSeed là các xâu bộ tám sao cho |MaskedSeed| = SeedLen; bước này sẽ thất bại nếu |C0| < SeedLen.
b) Đặt ![]() , bước này sẽ thất bại nếu EG không phải là mã hợp lệ của phần tử nhóm.
, bước này sẽ thất bại nếu EG không phải là mã hợp lệ của phần tử nhóm.
c) Tính ![]()
d) Đặt PEH = ε'(![]() ).
).
e) Đặt SeedMask = KDF(I1 || EG || PEH,SeedLen).
f) Đặt seed = MaskedSeed Å SeedMask.
g) Tính
![]()
là xâu bộ tám độ dài ![]()
h) Tạo cú pháp t, t = u || K ở đây u và K là xâu bộ tám thỏa mãn ![]() và |K| = KeyLen.
và |K| = KeyLen.
i) Tính r = OS2IP(u) mod μ.
j) Tính ![]() = r.g.
= r.g.
k) Kiểm tra ![]() , nếu không phải thì thất bại.
, nếu không phải thì thất bại.
I) Đưa ra khóa bí mật K.
CHÚ THÍCH Việc xem xét tính an toàn của lược đồ trên có thể tìm tại phụ lục B.10.
10.4. ACE-KEM
Điều này mô tả cơ chế bọc khóa ACE - KEM.
CHÚ THÍCH ACE - KEM được xây dựng dựa trên công trình của Cramer và Shoup [13,14].
10.4.1. Các tham số hệ thống
ACE - KEM là họ các cơ chế bọc khóa, được tham số hóa bởi các tham số hệ thống sau:
- G: nhóm cụ thể
![]()
được mô tả tại Điều 10.1;
- KDF: hàm xuất khóa được mô tả ở Điều 6.2;
- Hàm băm mật mã được mô tả ở Điều 6.1;
- CofactorMode: một trong hai giá trị 0 hoặc 1.
- KeyLen: số nguyên dương.
Bất kỳ sự kết hợp nào của các tham số hệ thống được phép đều cho phép, ngoại trừ các hạn chế sau:
- HashLen: phải nhỏ hơn log256μ.
- Nếu v = 1 thì CofactorMode sẽ bằng 0.
- Nếu v > 1 CofactorMode có thể bằng 1 với điều kiện gdc(μ, v) = 1.
CHÚ THÍCH Giá trị của Cofactormode chỉ được sử dụng bởi thuật toán giải mã.
10.4.2. Tạo khóa
Thuật toán tạo khóa ACE - KEM.KeyGen không có đầu vào, thực hiện như sau:
a) Tạo số ngẫu nhiên w,x,y,z Î [0...μ).
b) Tính các phần tử của nhóm
g' = w.g,c = x.g,d = y.g,h = z.g.
c) Đưa ra khóa công khai:
- g',c,d,h: các phần tử thuộc ![]()
d) Đưa ra khóa riêng:
- w,x,y,z: các số nguyên thuộc tập [0 ...μ).
10.4.3. Mã hóa
Thuật toán mã hóa ACE = KEM.Encrypt nhận đầu vào là khóa công khai, gồm
g',c,d,h Î ![]()
cùng tùy lựa chọn mật mã fmt xác định định dạng dùng để mã hóa phần tử nhóm. Thuật toán thực hiện như sau:
a) Tạo số ngẫu nhiên r Î [0…μ)
b) Tính các phần tử nhóm
u = r.g,u' = r.g',![]() = r.h.
= r.h.
c) Tính các xâu bộ tám
EU = ε(u,fmt),EU' = ε(u',fmt')
d) Tính số nguyên
α = OS2IP(Hash.eval(EU || EU')).
e) Tính số nguyên
r' = a.r mod μ.
f) Tính phần tử nhóm
v = r.c + r'.d.
g) Đặt EV= ε(v,fmt).
h) Đặt PEH = ε'(![]() ).
).
i) Đặt C0 = EU || EU' || EV.
j) Đặt K = KDF(EU || PEH,KeyLen).
k) Đưa ra là bản mã C0 và khóa bí mật K.
10.4.4. Giải mã
Thuật toán ACE - KEM.Decrypt nhận đầu vào là khóa bí mật, gồm w,x,y,zÎ [0...μ) và bản mã C0. Thuật toán chạy như sau:
a) Tạo cú pháp cho C0, C0 = EU || EU' || EV, ở đấy EU, EU', và EV là các xâu bộ tám sao cho đối với một số phần tử nhóm (xác định duy nhất) u,u',vÎ H, ta có u = ![]() (EU), u’ =
(EU), u’ = ![]() (EU'), v =
(EU'), v = ![]() (EV). Bước này sẽ thất bại nếu C0 không được tạo cú pháp như vậy.
(EV). Bước này sẽ thất bại nếu C0 không được tạo cú pháp như vậy.
b) Kiểm tra tập hợp {EU, EU', EV} có phải là tập bền vững các mã hợp lệ không, nếu không thì thất bại.
c) Nếu CofactorMode = 1, đặt
![]()
Ngược lại, thì đặt ![]() .
.
d) Nếu CofactorMode ≠ 1 và v > 1: kiểm tra u Î ![]() nếu u Ï
nếu u Ï ![]() thì thất bại.
thì thất bại.
e) Tính số nguyên
α = OS2IP(Hash. eval(EU || EU')).
f) Tính số nguyên ![]()
g) Kiểm tra
![]()
nếu không thỏa mãn, thì thất bại.
h) Tính phần tử nhóm ![]() .
.
i) Đặt PEH = ε'(![]() ).
).
j) Đặt K - KDF(EU || PEH, KeyLen).
k) Đưa ra là khóa bí mật K.
Vì lý do an toàn, khuyến cáo rằng việc thực thi không được để lộ bất kỳ thông tin nào về lý do sinh ra lỗi tại bước g. Nói riêng, việc thực thi có thể đưa ra cùng một thông báo lỗi tại cùng thời điểm bất kể lý do sinh ra lỗi.
CHÚ THÍCH 1 Sử dụng CofactorMode = 1 có thể mang lại lợi ích cho thực thi nếu v đủ nhỏ. Chú ý rằng ở chế độ này việc thực thi có thể tính toán trước và lưu trữ giá trị ![]() thay vì tính các giá trị w,x,y,z…
thay vì tính các giá trị w,x,y,z…
CHÚ THÍCH 2 Việc thực thi không phụ thuộc vào việc sử dụng phiên bản tương đương về chức năng sau đây của thuật toán giải mã. Trong thực thi không cần thiết phải tính u' và v tại bước a của thật toán giải mã, mà đơn giản là tạo ra cú pháp C0 sau khi nhận được EU, EU', và EV, và chỉ biến đổi EU thành phần tử nhóm u. Bước b có thể bỏ qua. Tiếp đó việc kiểm tra tại bước g của thuật toán giải mã thực hiện như sau: Nếu u = 0 thì kiểm tra EU' và EV có phải là mã (duy nhất) của 0 hay không; nếu không thì giả sử fmt là biến định dạng của EU và kiểm tra các điều kiện ε(![]() = EU' và ε(
= EU' và ε(![]() = EV.
= EV.
CHÚ THÍCH 3 Việc xem xét chi tiết tính an toàn của lược đồ này được đề cập ở Phụ lục B.11.
11. Mật mã phi đối xứng dựa trên RSA và các cơ chế bọc khóa
Điều này mô tả mật mã phi đối xứng và các cơ chế bọc khóa dựa trên biến đổi RSA. Mã RSAES được mô tả tại Điều 11.4; cơ chế bọc khóa RSA - KEM được mô tả ở Điều 11.5.
CHÚ THÍCH 1 Các lược đồ này là sự cải biên của lược đồ mật mã gốc RSA [31].
CHÚ THÍCH 2 Trong một số tiêu chuẩn ISO khác, thuật ngữ “phân tích số“ được sử dụng ở những nơi "dựa vào RSA"; tuy nhiên, vì tiêu chuẩn này xác định một số lược đồ khác nhau dựa trên phân tích số, nên nó chấp nhận thỏa thuận đặt tên mới.
11.1. Các thuật toán tạo khóa RSA
Thuật toán tạo khóa RSA, RSAKeyGen() là thuật toán xác suất không có đầu vào, đầu ra là bộ ba (n, e, d), ở đây:
- Số nguyên n là tích của hai số nguyên tố p và q, có độ dài tương tự nhau, p ≠ q,
- e là số nguyên dương thỏa mãn điều kiện gcd(e, (p - 1)(q -1)) = 1 và
- d là số nguyên dương thỏa mãn ed ≡ 1(modλ(n)) ở đây λ(n) là bội số chung nhỏ nhất của (p -1) và (q -1).
Phân phối đầu ra của thuật toán tạo khóa RSA phụ thuộc vào thuật toán cụ thể. Thuật toán này được phép cho kết quả đầu ra không thỏa mãn các điều kiện trên đây, chừng nào điều đó còn xảy ra với xác suất không đáng kể.
CHÚ THÍCH 1 Trong việc mô tả mật mã dựa trên RSA, các mật mã này được tham số hóa bằng thuật ngữ RSAKeyGen; ví dụ RSAKeyGen được coi như một tham số hệ thống của mật mã. Trong những thực thi thông thường, thuật toán tạo khóa cụ thể có thể được chọn từ họ các thuật toán, được tham số hóa bởi “tham số an toàn’ (ví dụ, độ dài của n).
CHÚ THÍCH 2 Xem ISO/IEC 18033 hướng dẫn thuật toán tạo các số nguyên tố p và q được đề cập trên đây.
11.2. Biến đổi RSA
Thuật toán RSATransform (X, α, n) nhận đầu vào là
- Xâu bộ tám X,
- Số nguyên α, và
- Số nguyên n,
Và đầu ra là xâu bộ tám. Thuật toán thực hiện như sau:
a) Kiểm tra việc thực hiện |X| = ![]() (n); nếu không thực hiện thì thất bại.
(n); nếu không thực hiện thì thất bại.
b) Đặt x = OS2IP(X).
c) Kiểm tra x < n; nếu không thỏa mãn thì thất bại.
d) Đặt y = xa mod n.
e) Đặt Y = OS2IP(y,![]() (n)).
(n)).
f) Đưa ra là Y.
CHÚ THÍCH Như đã biết, nếu (n, e, d) là đầu ra của thuật toán tạo khóa RSA và X = I2OSP(x,![]() (n)) với số nguyên x nào đó thỏa mãn 0 ≤ x ≤ n, khi đó
(n)) với số nguyên x nào đó thỏa mãn 0 ≤ x ≤ n, khi đó
RSATransform (RSATransform(X,e,n),d,n) = X.
11.3. Các cơ chế mã hóa RSA
Cơ chế mã hóa RSA, REM xác định hai thuật toán:
- REM.Encode(M, L, ELen) nhận đầu vào là bản rõ M, nhãn L và độ dài đầu ra là ELen. Ở đây, M và L là các xâu bộ tám với độ dài bị hạn chế được mô tả dưới đây. Đầu ra là xâu bộ tám E độ dài Elen.
- REM.Decode(E,L) nhận đầu vào là xâu bộ tám E, nhãn L và tìm bản rõ M thỏa mãn REM.Encode(M,L,|E|) = E. Nếu không đưa ra được M như vậy thì thất bại.
Ngoài ra, cơ chế cũng nên xác định giới hạn REM.Bound, sao cho khi gọi REM.Encode(M,L,ELen), thì điều kiện |M| ≤ ELen - REM sẽ được thỏa mãn. Nếu không thuật toán mã hóa sẽ thất bại. Ngoài ra thuật toán mã hóa cũng có thể thất bại, nếu |L| vượt quá giới hạn được xác định bởi quá trình thực thi.
Nói chung thuật toán REM.Encode là thuật toán xác suất, bởi cùng một bản rõ có thể được mã hóa bằng một số cách khác nhau. Đồng thời vì lý do kỹ thuật, yêu cầu bộ tám đầu tiên của đầu ra phải là Oct(0).
11.3.1. Các cơ chế mã hóa RSA được phép
Trong phần này của ISO/IEC, Cơ chế mã hóa RSA được phép là REM1, được mô tả dưới đây ở Điều 11.3.2.
11.3.2. REM1
Điều này mô tả cơ chế mã hóa cụ thể được gọi là REM1.
CHÚ THÍCH REM1 được xây dựng trên cơ sở OAEP của Bellare và Rogaway [8].
11.3.2.1. Các tham số hệ thống
REM1 là họ các cơ chế mã hóa RSA được tham số hóa bởi các tham số hệ thống sau đây:
- Hash: hàm băm mật mã được mô tả tại Điều 6.1;
- KDF: hàm dẫn xuất khóa được mô tả ở Điều 6.2.
Giá trị REM.Bound được xác định bằng:
REM1.Bound = 2.Hash.len + 2.
11.3.2.2. Hàm mã hóa
Hàm mã hóa REM1.Encode(M, L, ELen) chạy như sau:
a) Kiểm tra |M| ≤ ELen-2.HashJen-2, nếu không thì thất bại.
b) Giả sử phần đệm (pad) là xâu bộ tám độ dài ELen-|M|-2.Hash.Ien-2 gồm một xâu bộ tám Oct(0).
c) Tạo mầm là xâu bộ tám ngẫu nhiên mầm độ dài Hash.len.
d) Đặt check = Hash.eval(L).
e) Đặt DataBlock = check ![]()
f) Đặt DataBlockMask = KDF(seed, Elen - Hash.len - 1).
g) Đặt MaskedDataBlock = DataBlockMask Å DataBlock.
h) Đặt SeedMask = KDF(MaskedDataBlock, Hash.len).
i) Đặt MaskedSeed = SeedMask Å seed.
j) Đặt E = ![]() || MaskedSeed || MaskedDataBlock.
|| MaskedSeed || MaskedDataBlock.
k) Đưa ra E.
11.3.2.3. Hàm giải mã (Decoding function)
Thuật toán REM1.Decode(E,L) chạy như sau:
a) Giả sử Elen = |E|.
b) Kiểm tra ELen ≥ 2.Hash.len + 2; nếu không thì thất bại.
c) Đặt Check = Hash.eval(L).
d) Tạo cú pháp E, E = ![]() || MaskedSeed || MaskedDataBlock; ở đây X là bộ tám và MaskedSeed và MaskedDataBlock là các bộ tám thỏa mãn hệ thức
|| MaskedSeed || MaskedDataBlock; ở đây X là bộ tám và MaskedSeed và MaskedDataBlock là các bộ tám thỏa mãn hệ thức
|MaskedSeed| = Hash.len,|MaskedDataBlock| = Elen-Hash.len-1.
e) Đặt SeedMask = KDF(MaskedDataBlock, Hash.len).
f) Đặt seed = MaskedSeed Å SeedMask.
g) Đặt DataBlockMask = KDF(seed,Elen - Hash.len - 1).
h) Đặt DataBlock = MaskedDataBlock Å DataBlockMask.
i) Tạo cú pháp cho DataBlock, DataBlock=check'![]() ; Check’ và M' là các xâu bộ tám với |check'| = Hash.len;|M'| = ELen-2.Hash.len-1.
; Check’ và M' là các xâu bộ tám với |check'| = Hash.len;|M'| = ELen-2.Hash.len-1.
j) Giả sử ![]() là các bộ tám và l - Elen - 2.Hash.len - 1; đồng thời giả sử m là số nguyên dương lớn nhất sao cho m ≤ l, và M1 = M2 =
là các bộ tám và l - Elen - 2.Hash.len - 1; đồng thời giả sử m là số nguyên dương lớn nhất sao cho m ≤ l, và M1 = M2 = ![]() = Oct(0) và T là ký hiệu bộ tám Mm, giả sử M là ký hiệu xâu bộ tám
= Oct(0) và T là ký hiệu bộ tám Mm, giả sử M là ký hiệu xâu bộ tám ![]() .
.
k) Nếu check’ ≠ check, X ≠ Oct(0), hoặc T ≠ Oct(1) thì thất bại.
l) Đưa ra M.
Vì lý do an toàn, điều quan trọng là trong quá trình thực thi không để lộ bất kỳ thông tin nào về nguyên nhân phát sinh lỗi tại bước k. Nói riêng, thực thi có thể cho ra thông báo cùng lỗi tại cùng thời điểm, bất kể nguyên nhân việc sinh ra lỗi.
11.4. RSAES
11.4.1. Các tham số hệ thống
RSAES là họ các mã phi đối xứng với độ dài bản rõ bị hạn chế, được tham số hóa bởi các tham số hệ thống sau:
- RSAKeyGen: Thuật toán tạo khóa RSA được mô tả tại Điều 11.1;
- REM: cơ chế mã hóa RSA được mô tả tại Điều 11.3.
Bất kỳ một tổ hợp các tham số hệ thống nào cũng được phép với các hạn chế sau:
- Độ dài tính bằng octet của đầu ra n của RSAKeyGen() phải luôn luôn lớn hơn REM.Bound.
11.4.2. Tạo khóa
Thuật toán RSAES.KeyGen không có đầu vào, chạy như sau:
a) Tính (n, e,d) = RSAKeyGen().
b) Khóa công khai đầu ra PK:
- n: số nguyên dương.
- e: số nguyên dương.
c) Đưa ra khóa riêng pk:
- n: số nguyên đương.
- d: số nguyên dương.
RSAES là mật mã phi đối xứng với độ dài bản rõ bị hạn chế. Đối với khóa công khai cho trước PK = (n, e), giá trị của RSAES.MaxMsgLen(PK) là ![]() (n) - REM. Bound.
(n) - REM. Bound.
Các thuật toán mã hóa và giải mã đều sử dụng biến đổi thuật toán RSA được định nghĩa tại Điều 11.2.
11.4.3. Mã hóa
Thuật toán RSAES.Encrypt nhận đầu vào;
- Khóa công khai, gồm số nguyên dương n và số nguyên dương e,
- Nhãn L,
- Bản rõ M với độ dài lớn nhất ![]() (n) - REM.Bound, và
(n) - REM.Bound, và
- Không có tùy chọn mật mã.
Thuật toán chạy như sau:
a) Đặt E = REM.Encode(M, L,![]() (n)).
(n)).
b) Đặt C = RSATransform(E, e, n).
c) Đưa ra C.
11.4.4. Giải mã
Thuật toán RSAES.Decrypt nhận đầu vào:
- Khóa riêng, gồm số nguyên dương n và số nguyên dương e,
- Nhãn L, và
- Bản mã C.
Thuật toán chạy như sau:
a) Đặt E = RSATransform (C,d,n); chú ý rằng bước này cũng có thể thất bại.
b) Đặt M = REM. Decode(E,L); chú ý rằng bước này cũng có thể thất bại.
c) Đưa ra M.
CHÚ THÍCH Tính an toàn của RSAES được xem xét tại Phụ lục B.13.
11.5. RSA-KEM
11.5.1. Các tham số hệ thống
RSA - KEM là họ các cơ chế bọc khóa, được tham số hóa bởi các tham số hệ thống sau đây:
- RSAKeyGen: Thuật toán tạo khóa RSA, được mô tả ở Điều 11.1;
- KDF: hàm dẫn xuất khóa được mô tả ở Điều 6.2;
- KeyLen: số nguyên dương.
Giá trị của RSA - KEM.KeyLen được xác định bằng giá trị của tham số hệ thống Keylen.
11.5.2. Tạo khóa
Thuật toán RSA - KEM.KeyGen không có đầu vào, chạy như sau:
a) Tính (n,e,d) = RSAKeyGen().
b) Đưa ra khóa công khai PK:
- n: số nguyên dương.
- e: số nguyên dương.
c) Đưa ra khóa riêng pk:
- n: số nguyên dương.
- d: số nguyên dương.
Thuật toán mã hóa và giải mã sử dụng thuật toán biến đổi RSA được định nghĩa tại Điều 11.2.
11.5.3. Mã hóa
Thuật toán mã hóa RSA - KEM.Encrypt nhận đầu vào là:
- Khóa công khai, bao gồm các số nguyên dương n và e, và
- Không có tùy chọn mật mã.
Thuật toán chạy như sau:
a) Tạo số ngẫu nhiên r Î [0..n).
b) Đặt R = I2OSP(r,![]() (n)).
(n)).
c) Đặt C0 = RSATransform(R, e,n).
d) Tính K = KDF(R,KeyLen).
e) Đưa ra là bản rõ C0 và khóa bí mật K.
11.5.4. Giải mã
Thuật toán RSA - KEM.Decrypt nhận đầu vào:
- Khóa mật gồm các số nguyên dương n và d
- Bản mã C0.
Thuật toán chạy như sau:
a) Đặt R = RSATransform(C0, d, n); chú ý rằng bước này cũng có thể thất bại.
b) Tính K = KDF(R, KeyLen).
c) Đầu ra là khóa bí mật K.
CHÚ THÍCH Tính an toàn của RSA - KEM được xem xét tại phụ lục B.14.
12. Mật mã dựa trên phép bình phương modulo
Điều này mô tả họ các mật mã phi đối xứng dựa trên phép bình phương modulo. Mã HIME(R) được mô tả tại Điều 12.3.
12.1. Các thuật toán tạo khóa HIME
Với số dương l và d >1 và thuật toán tạo khóa l - bit HIME - HIMEKeyGen là thuật toán xác suất không có đầu vào, đầu ra là các số nguyên dương (p,q,n,d),ở đấy:
- p là số nguyên tố, với 2l-1 ≤ p < 2l; p ≡ 3 (mod 4),
- q là số nguyên tố với 2l-1 ≤ q < 2l; q ≡ 3 (mod 4) và p ≠ q,
- n = pdq.
Phân phối đầu ra của thuật toán tạo khóa HIME bit phụ thuộc vào thuật toán cụ thể. Thuật toán này được phép cho kết quả đầu ra không thỏa mãn các điều kiện trên đây, chừng nào điều đó còn xảy ra với xác suất không đáng kể.
CHÚ THÍCH 1 Trong mô tả mật mã dựa trên HIME, những lược đồ này được tham số hóa theo thuật ngữ của HIMEKeyGen, nghĩa là HlMEKeyGen được xem như tham số hệ thống của mật mã.
CHÚ THÍCH 2 Tham khảo ISO/IEC 18032 về hướng dẫn thiết kế thuật toán tạo các số nguyên tố p và q ở trên.
12.2. Các cơ chế mã hóa HIME
Cơ chế mã hóa theo HIME, ký hiệu HIME là HEM đưa ra hai thuật toán:
- HEM.Encode(M,L,ELen,KLen) nhận đầu vào là bản rõ M, nhãn L, độ dài đầu ra Elen, và số nguyên dương KLen.M và L là các xâu bộ tám với độ dài bị giới hạn, được mô tả dưới đây. KLen thỏa mãn điều kiện 1 ≤ KLen ≤ 8. Đầu ra là xâu bộ tám E độ dài ELen.
- HEM.Decode(E,L,KLen) nhận đầu vào là xâu bộ tám E, nhãn L, và số nguyên dương KLen. Đầu ra là bản rõ M sao cho HEM.Encode(M,L,|E|,KLen) = E. Thuật toán sẽ đưa ra M, nếu không thì thất bại.
12.2.1. Các cơ chế mã hóa HIME được phép
Trong phần này của ISO/IEC 18033, cơ chế mã hóa HIME được phép là HEM1, được mô tả ở Điều 12.2.2 dưới đây.
12.2.2. HEM1
Điều này mô tả một cơ chế mã hóa HIME cụ thể, được gọi là HEM1.
CHÚ THÍCH HEM1 dựa trên OAEP do Bellare và Rogaway xây dựng [8].
12.2.2.1. Các tham số hệ thống
HEM1 là họ các cơ chế mã hóa HEM được tham số hóa bởi các tham số hệ thống sau:
- Hash: hàm băm mật mã được mô tả tại Điều 6.1;
- KDF: hàm dẫn xuất khóa được mô tả tại Điều 6.2.
Độ lớn của HEM1.Bound được định nghĩa bằng
MEM1.Bound = 2.Hash.len + 2.
12.2.2.2. Hàm mã hóa
Thuật toán HEM1.Encode(M,L,ELen,KLen) chạy như sau:
a) Kiểm tra điều kiện |M| ≤ ELen-2.HashJen-2, nếu không thỏa mãn thì thất bại.
b) Giả sử phần pad là xâu bộ tám độ dài ELen-|M|-2Hash.len-2 gồm một xâu octet Oct(0).
c) Tạo xâu bộ tám ngẫu nhiên seed với độ dài Hash.len +1.
d) Xóa đi KLen - bít có nghĩa nhất của seed.
e) Đặt check = Hash.eval(L).
f) Đặt Data.Block = ![]()
g) Đặt DataBlockMask = KDF(seed, ELen - HashLen - 1).
h) Đặt MaskedDataBlock = DataBlockMask Å DataBlock.
i) Đặt SeedMask = KDF(MaskedDataBlock,Hash.len + 1).
j) Xóa đi KLen - bit có nghĩa nhất của SeedMask.
k) Đặt MaskedSeed = SeedMask Å seed.
I) Đặt E = MaskedSeed II MaskedDataBlock.
m) Đưa ra E.
12.2.2.3. Hàm giải mã
Thuật toán HEM1.Decode(E,L,KLen) chạy như sau:
a) Đặt ELen = |E|.
b) Đặt check = Hash.eval(L).
c) Tạo cú pháp E, E = MaskedSeed II MaskedDataBlock, MaskedDataBlock và MaskedSeed là các xâu bộ tám thỏa mãn điều kiện |MaskedSeed| = Hash.len +1 và |MaskedDataBlock| = Elen - Hash.len - 1.
d) Đặt SeedMask = KDF(MaskedDataBlock, Hash.len + 1).
d) Xóa Klen - bit có nghĩa nhất của SeedMask.
f) Đặt seed = MaskedSeed Å SeedMask.
g) Đặt DataBlockMask = KDF(seed,ELen - Hash.len - 1).
h) Đặt DataBlock = MaskedDataBlock Å DataBlockMask.
i) Tạo cú pháp cho DataBlock, DataBlock = check'||M' ở đây check’ và M’ là các xâu bộ tám thỏa mãn điều kiện |check'| = Hash.len và |M'| = ELen - 2.Hash.len - 1.
j) Đặt M’ = ![]() ,ở đây M1,…,Ml là các bộ tám và l = Elen - 2.Hash. len - 1; đồng thời giả sử m là số nguyên dương lớn nhất sao cho m ≤ /, và M1 = M2 =...= Mm-1= Oct(0) và T là ký hiệu Mm, M ký hiệu xâu bộ tám
,ở đây M1,…,Ml là các bộ tám và l = Elen - 2.Hash. len - 1; đồng thời giả sử m là số nguyên dương lớn nhất sao cho m ≤ /, và M1 = M2 =...= Mm-1= Oct(0) và T là ký hiệu Mm, M ký hiệu xâu bộ tám ![]()
k) Nếu check' ≠ check, phần KLen - bit có nghĩa nhất nhất của seed ≠ xâu bit gồm các số 0, hoặc T ≠ Oct(1), thì thất bại.
l) Đưa ra M.
Vì lý do an toàn, điều quan trọng là trong quá trình thực thi không để lộ bất kỳ thông tin nào về nguyên nhân phát sinh lỗi tại bước k. Nói riêng, việc thực thi có thể đưa ra cùng thông báo lỗi tại cùng thời điểm bất kể nguyên nhân sinh ra lỗi.
12.3. HIME(R)
12.3.1. Các tham số hệ thống
HIME(R) là họ các mật mã phi đối xứng với độ dài bản rõ bị hạn chế, được tham số hóa bởi các tham số hệ thống sau:
- d: số nguyên >1,
- HIMEKeyGen: thuật toán tạo khóa HIME l-bit được mô tả tại Điều 12.1;
- HEM: cơ chế mã hóa HIME được mô tả ở Điều 12.2.
12.3.2. Tạo khóa
Thuật toán HIME(R).KeyGen không có đầu vào, chạy như sau:
a) Tính (p,q,n) = HIMEKeyGen().
b) Đưa ra khóa công khai PK:
- n: số nguyên dương.
c) Đưa ra khóa riêng pk:
- n, p, q: các số nguyên dương.
12.3.3. Mã hóa
Thuật toán mã hóa HIME(R).Encrypt nhận đầu vào là
- khóa công khai là số nguyên dương n,
- Nhãn L,
- Bản rõ M với độ dài lớn nhất là ![]() (n) - HEM.Bound, và
(n) - HEM.Bound, và
- Không có tùy chọn mật mã.
Thuật toán chạy như sau:
a) Đặt k = 8.![]() (n) - (độ dài bit của n) + 1.
(n) - (độ dài bit của n) + 1.
b) Đặt E = HEM.Encode(M, L,![]() (n), k).
(n), k).
c) Đặt e = OS2IP (E).
d) Đặt c = e2mod n.
e) Đặt C = I2OSP(c,![]() (n)).
(n)).
f) Đưa ra C.
12.3.4. Giải mã
Thuật toán giải mã HIME(R).Decrypt nhận đầu vào là:
- Khóa riêng gồm các số nguyên dương n, p, q,
- Nhãn L,
- Bản mã C.
Thuật toán chạy như sau:
a) Đặt c = OS2IP(C).
b) Đặt k= 8.![]() (n)-(độ dài bit của n) + 1.
(n)-(độ dài bit của n) + 1.
c) Đặt z = p-1 mod. q.
d) Đặt cp = c mod p, cq= c mod q.
e) Đặt α1 = ![]() mod p,α2 = p - α1.
mod p,α2 = p - α1.
f) Đặt β1 = ![]() mod q,β2 = q - β1
mod q,β2 = q - β1
g) Đặt
1) ![]() và
và ![]() z mod q.
z mod q.
2) ![]() và
và ![]() z mod q.
z mod q.
3) ![]() và
và ![]() z mod q.
z mod q.
4) ![]() và
và ![]() z mod q.
z mod q.
h) Với i từ 1 đến 4, thực hiện:
1) Đặt ![]()
2) Với t từ 2 đến d, thực hiện:
i) Đặt ![]()
ii) Đặt ![]()
3) Đặt ![]()
i) Với i từ 1 đến 4, đặt Xi = I2OSP (xi,![]() (n)).
(n)).
j) Nếu tồn tại duy nhất i sao cho HEM.Decode(Xi,L, k) không bị thất bại và ![]() mod n = c, thì với i đó đặt M = HEM.Decode(Xi,L,k), nếu không thì thất bại.
mod n = c, thì với i đó đặt M = HEM.Decode(Xi,L,k), nếu không thì thất bại.
k) Đưa ra M.
CHÚ THÍCH Việc xem xét tính an toàn của lược đồ này được trình bày tại Phụ lục B.15.
PHỤ LỤC A
(Quy định)
CÚ PHÁP ASN.1 CHO CÁC BỘ ĐỊNH DANH ĐỐI TƯỢNG
Phụ lục cung cấp cú pháp cho các bộ định danh đối tượng, khóa công khai, và các cấu trúc tham số đi kèm với các thuật toán được đặc tả trong phần này của ISO/IEC 18033.

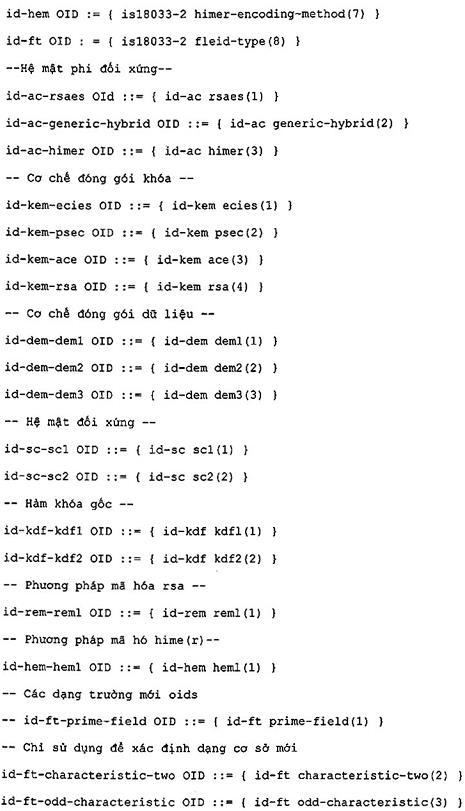











PHỤ LỤC B
(Tham khảo)
XEM XÉT TÍNH AN TOÀN
Trong Phụ lục này xem xét các đặc tính an toàn của các lược đồ mật mã khác nhau đã được mô tả trong phần này của tiêu chuẩn ISO/IEC 18033. Đối với mỗi loại lược đồ (ví dụ, mã phi đối xứng, thuật toán MAC,...) đưa ra định nghĩa hình thức tương ứng và với mỗi lược đồ cụ thể sẽ xem xét phạm vi mà định nghĩa đưa ra được thỏa mãn.
Tính an toàn của mỗi lược đồ có thể được chứng minh một cách hình thức, dựa trên các giả thuyết nhất định về tính khó, hoặc trên một giả thuyết khác là các cơ chế ở mức thấp hơn là an toàn. Các chứng minh này là “các phép quy dẫn”, trong đó chỉ ra làm thế nào để quy dẫn vấn đề kẻ địch A phá được lược đồ về lược đồ kẻ địch A' giải bài toán được giả thiết là khó, hoặc phá một cơ chế được coi là an toàn. Trong phần lớn các trường hợp, “chất lượng" của "phép quy dẫn" được chỉ ra bằng mô tả cách định lượng mối quan hệ giữa các yêu cầu về tài nguyên (ví dụ thời gian chạy thuật toán) và ưu thế (ví dụ xác suất thành công) của A và yêu cầu về tài nguyên và ưu thế của A'. Phép quy dẫn được gọi là “chặt chẽ”, nếu các yêu cầu về tài nguyên của A' lớn hơn không đáng kể so với các yêu cầu về tài nguyên của A, và nếu ưu thế của A' cũng nhỏ hơn không đáng kể so với của A.
Phương pháp tiếp cận tính an toàn ở đây là “cụ thể", như trong [6], so với cách tiếp cận có tính ‘‘tiệm cận”: phép quy dẫn của tính an toàn được phát biểu bằng thuật ngữ của các lược đồ cụ thể, chứ không phải bằng thuật ngữ của họ các lược đồ được chỉ số hóa bởi “tham số an toàn” và chỉ số này có xu hướng tiến ra vô cùng. Tuy nhiên, một số ước lượng định lượng được biểu thị bằng khái niệm “O lớn”, nhưng hoàn toàn là những hằng số bé.
Một số chứng minh tính an toàn thuộc mô hình được gọi là “tiên tri ngẫu nhiên”, mô hình này đầu tiên được hình thức hóa trong [7] và từ đó được sử dụng để phân tích nhiều lược đồ mật mã. Trong mô hình tiên tri ngẫu nhiên, hàm băm và hàm dẫn xuất khóa được mô hình như những hàm ngẫu nhiên, mà đối với mọi thuật toán hay mọi kẻ tấn công, chúng chỉ là những “hộp đen". Các loại chứng minh tính an toàn theo mô hình tiên tri ngẫu nhiên như thế tốt nhất là nên xem như những chứng minh mới ở mức tìm tòi (heuristic). Có thể, một lược đồ là an toàn theo mô hình tiên tri ngẫu nhiên, nhưng lại bị phá mà không cần giải được bài toán khó cơ sở, hoặc các giả thuyết an toàn và không cần phải tìm ra bất kỳ điểm yếu cụ thể nào trong hàm băm hay hàm dẫn xuất khóa nào [12]. Nối cách khác, chứng minh tiên tri ngẫu nhiên đã loại bỏ mất một lớp tấn công rộng.
B.1. Thuật toán MAC
Điều này mô tả đặc tính an toàn cơ bản của thuật toán MAC đă được trình bày trong phần này của tiêu chuẩn ISO/IEC 18033.
Xét thuật toán MA thuộc các thuật toán MAC được mô tả tại Điều 6.3.
Xét kịch bản tấn công sau đây. Kẻ tấn công chọn ngẫu nhiên một xâu bộ tám T* và khóa bí mật k'. Giả sử kẻ tấn công cũng sở hữu giá trị MAC* = MA.eval(k',T*). Kẻ tấn công tạo ra một danh sách các cặp (T, MAC), ở đây T là xâu bộ tám với T ≠ T* (và cũng không nhất thiết có cùng độ dài với T), và MAC là xâu bộ tám độ dài MA.MACLen. Ưu thế của kẻ tấn công được định nghĩa là xác suất sao cho với mỗi cặp (T, MAC), ta có MA.eval(k',T) = MAC.
Với kẻ tấn công A và thuật toán MA, lợi thế được ký hiệu là AdvMA(A). Nếu kẻ tấn công chạy trong khoảng thời gian nhiều nhất là t và tạo ra được một danh sách nhiều nhất là l cặp và T* và tất cả T về độ dài bị giới hạn bởi l', thì A được gọi là kẻ tấn công MA[t, l, l'].
Tính an toàn ở đây có nghĩa là lợi thế này là không đáng kể đối với bất kỳ kẻ tấn công hiệu quả nào.
Mặc dù mô hình tấn công “đơn thông báo' ở đây được xem là đủ cho việc thiết kế các cơ chế bọc dữ liệu an toàn, nhưng với nhiều ứng dụng khác là không đủ, và cần xem xét cả mô hình tấn công "đa thông báo“. Trong mô hình tấn công “đa thông báo”, thay vì thu được giá trị của MA.eval(k',.) tại đầu vào đơn lẻ T*, kẻ tấn công được phép thu được giá trị của MA.eval(k',.) tại nhiều đầu vào (được chọn phù hợp), T*1,…,T*s. Vì trước đó kẻ tấn công đã lập được danh sách các cặp (T, MAC), nhưng với hạn chế là ![]() với 1 ≤ i ≤ s
với 1 ≤ i ≤ s
Điều 6.3.1 cho phép sử dụng các thuật toán MAC được mô tả tại ISO/IEC 9797-1 và ISO/IEC 9797-2, tất cả các thuật toán này được thiết kế an toàn trong mô hình tấn công “đa thông báo' và một số trong số đó được chứng minh là an toàn theo mô hình này, dựa trên những giả thiết nhất định về hàm băm mật mã cơ sở.
B.2. Mã khối
Điều này mô tả đặc tính an toàn cơ bản của mã khối được trình bày trong phần này của ISO/IEC 18033.
Xét mã khối BC được xác định trong Điều 6.4.
BC được gọi là hoán vị giả ngẫu nhiên, nếu kẻ tấn công khó phân biệt được hoán vị ngẫu nhiên của xâu bộ tám độ dài BC.BlockLen với hoán vị b → BC.Encrypt(k,b) với khóa bí mật k được chọn ngẫu nhiên. Trong tấn công này, kẻ tấn công được cho ở dạng tiếp cận tiên tri (oracle access) tới hoán vị hoặc tới hoán vị ngẫu nhiên hoặc tới mã khối và phải đoán được đang tiếp cận trường hợp nào. Hoán vị được coi là giả ngẫu nhiên, nếu với bất kỳ kẻ tấn công hiệu quả nào, khả năng đoán thành công của nó gần bằng 1/2, với sai số không đáng kể.
Điều 6.4.1 cho phép sử dụng các mã khối được mô tả trong ISO/IEC 18033-3. Mặc dù có một ít chứng minh hình thức, nhưng kinh nghiệm cho thấy những mã khối này trong thực tế cũng hành xử như các phép hoán vị giả ngẫu nhiên.
B.3. Mã đối xứng
Điều này mô tả đặc tính an toàn cơ bản được yêu cầu đối với mã đối xứng trong phần này của ISO/IEC 18033.
Xét mã đối xứng MC được xác định trong Điều 6.5.
Xét kịch bản tấn công sau. Kẻ tấn công tạo ra hai bản rõ (hai xâu bộ tám) M0, M1 có độ dài bằng nhau, khóa bí mật k và chọn một bit ngẫu nhiên b, và Mb được mã hóa theo khóa k. Kẻ tấn công biết bản mã c. Gọi ![]() là phỏng đoán bit b của kẻ tấn công. Ưu thế của kẻ tấn công được định nghĩa bằng
là phỏng đoán bit b của kẻ tấn công. Ưu thế của kẻ tấn công được định nghĩa bằng ![]()
Giả sử A là kẻ tấn công và SC là mã đối xứng, ưu thế của A được ký hiệu là AdvSC(A). Nếu kẻ tấn công chạy thời gian nhiều nhất là t và đầu ra của thuật toán mã hóa có độ dài lớn nhất là l bộ tám, thì A được gọi là kẻ tấn công SC[t, l].
Tính an toàn ở đây có nghĩa là ưu thế này là không đáng kể đối với bất kỳ kẻ tấn công hiệu quả nào.
Mặc dù mô hình tấn công "đơn bản rõ" ở đây được xem là đủ cho việc thiết kế các cơ chế bọc dữ liệu an toàn, nhưng với nhiều ứng dụng khác là không đủ và cần xem xét thêm mô hình tấn công “đa bản rõ”, ở đó kẻ tấn công được phép có được nhiều phép mã hóa phù hợp để lựa chọn. Dạng tấn công này cũng được gọi là tấn công “chọn bản rõ”. Một dạng tấn công khác được gọi là tấn công “chọn bản mã”, ở đó kẻ tấn công có được kết quả giải mã các bản mã đã lựa chọn.
B.3.1. An toàn của SC1
Điều này xem xét tính an toàn của SC1 được định nghĩa tại Điều 6.5.2.
Đấy là mã đối xứng được tham số hóa theo thuật ngữ của mã khối BC.
Chế độ móc xích mã khối mã (CBC) với giá trị khởi đầu (IV) được phân tích trong [4], tại đây đã chỉ ra chế độ CBC là an toàn đối với tấn công “đa bản rõ” như đã thảo luận ở trên, với giả thiết BC là hoán vị giả ngẫu nhiên (xem Phụ lục B.2). Mã SC1 sử dụng giá trị khởi đầu cố định. Tuy vậy, dễ dàng điều chỉnh chứng minh tính an toàn trong [4] để chỉ ra rằng SC1 là an toàn chống lại tấn công "đơn bản rõ” vốn phù hợp với các cấu trúc trong tài liệu này.
Để ý rằng trong bài báo [35] trình bày một số tấn công lên SC1. Tuy nhiên, các tấn công trong [35] là tấn công “chọn bản mã” và do đó không liên quan ở đây. Tóm lại lược đồ bộ đệm (padding) đóng vai trò an toàn trong mã hóa CBC chỉ khi xem xét các tấn công chọn bản mã.
B.3.2. An toàn của SC2
Phần này thảo luận tính an toàn của SC2 được định nghĩa trong Điều 6.5.3.
Hiện nay chưa có một phép quy dẫn hình thức nào quy tính an toàn của SC2 về tính an toàn của một số cơ chế khác hoặc tính khó của bài toán khác. Tuy nhiên, nếu muốn mô hình hóa hàm dẫn xuất khóa như một tiên tri ngẫu nhiên thì có thể yên tâm rằng SC2 là mật mã đối xứng an toàn.
B.4. Mật mã phi đối xứng
Điều này mô tả đặc tính an toàn cơ bản được yêu cầu đối với mật mã phi đối xứng.
Xét mật mã phi đối xứng AC, được định nghĩa ở Điều 7.
Xét kịch bản tấn công “chọn bản mã phù hợp” sau đây.
Bước 1: Chạy thuật toán tạo khóa, tạo ra khóa công khai và khóa riêng. Kẻ tấn công, hiển nhiên, biết được khóa công khai nhưng không biết khóa riêng.
Bước 2: Kẻ tấn công đưa ra một loạt câu truy vấn tùy ý để tiên tri giải mã. Mỗi câu chất vấn là một cặp nhãn/bản mã (L, C), cặp này được giải mã bởi tiên tri giải mã sử dụng khóa riêng. Kết quả giải mã được trao cho kẻ tấn công. Ngoài ra, nếu thuật toán thất bại thì thông tin này được trao cho kẻ tấn công và việc tấn công được tiếp tục. Kẻ tấn công tự do thiết kế các cặp nhãn/bản mã này theo một cách tùy ý - hiển nhiên không cần sử dụng thuật toán mã hóa để tính toán chúng.
Bước 3: Kẻ tấn công chuẩn bị nhãn L* và hai bản rõ “đích" M0, M1 có cùng độ dài, và nạp chúng vào tiên tri mã hóa. Nếu lược đồ hỗ trợ các tùy chọn mật mã nào đó, thì kẻ tấn công cũng sẽ chọn chúng. Tiên tri mã hóa chọn ngẫu nhiên b Î {0,1} mã hóa Mb sử dụng nhãn L*, chuyển kết quả là bản mã "đích" C* cho kẻ tấn công.
Bước 4: Kẻ tấn công tiếp tục chuyển cặp nhãn /bản mã (L,C) tới tiên tri giải mã, chỉ với điều kiện ràng buộc là (L,C) ≠ (L*,C*).
Bước 5: Kẻ tấn công đưa ra ![]() Î {0,1}, và dừng lại.
Î {0,1}, và dừng lại.
Ưu thế của A được định nghĩa bằng giá trị ![]() . Với kẻ tấn công A và mã phi đối xứng AC, ưu thế của A được ký hiệu là AdvAC(A). Nếu kẻ địch trong thời gian thực hiện t, thực hiện nhiều nhất là q truy vấn giải mã tiên tri, tất cả các bản mã là đầu ra từ mã hóa tiên tri và đầu vào của giải mã tiên tri có độ dài lớn nhất là l, và các nhãn đầu vào của mã hóa và giải mã tiên tri lớn nhất là l', khi đó A được gọi là kẻ tấn công -AC[t,q,l,l'].
. Với kẻ tấn công A và mã phi đối xứng AC, ưu thế của A được ký hiệu là AdvAC(A). Nếu kẻ địch trong thời gian thực hiện t, thực hiện nhiều nhất là q truy vấn giải mã tiên tri, tất cả các bản mã là đầu ra từ mã hóa tiên tri và đầu vào của giải mã tiên tri có độ dài lớn nhất là l, và các nhãn đầu vào của mã hóa và giải mã tiên tri lớn nhất là l', khi đó A được gọi là kẻ tấn công -AC[t,q,l,l'].
Tính an toàn có nghĩa là ưu thế đối với tất cả kẻ tấn công hiệu quả là không đáng kể.
Định nghĩa này, ở dạng hơi khác một ít, lần đầu tiên được đề xuất bởi Rackoft và Simon trong [30], trong công trình này định nghĩa trên đã được khái quát cho trường hợp độ dài bản rõ tùy ý và tính đến vai trò của nhãn. Nói chung cộng đồng nghiên cứu mật mã nhất trí rằng đây là thuộc tính an toàn “ổn" cho mật mã phi đối xứng tổng quát. Khái niệm an toàn này kéo theo các đặc tính có lợi khác như “không dễ uốn” (xem [15,16]). Một cách trực quan, tính không dễ uốn có nghĩa là khó biến đổi một cặp nhãn/bản mã (L,C), mã hóa bản rõ M thành cặp khác (L’,C’), sao cho việc giải mã C' bằng nhãn L' liên quan đến M theo một cách nào đó. Tham khảo thêm các khái niệm khác an toàn đối với mã đối xứng trong [11,14, 5,15,16]
Trong [27] trình bày một định nghĩa yếu hơn về an toàn, đôi lúc được gọi là an toàn chống lại các tấn công “thời gian ăn trưa". Trong thiết kế này, an toàn cũng được định nghĩa giống như ở trên, chỉ trừ một điểm là kẻ tấn công không được phép thực hiện bất kỳ truy vấn tiên tri giải mã nào ở bước 4. Mặc dù, điều này có vẻ giống với một định nghĩa tự nhiên về an toàn, song nó lại không tương thích với nhiều ứng dụng và không phải là khái niệm an toàn phù hợp cho các mã phi đối xứng với mục tiêu tổng quát.
Ngoài ra trong [21] cũng trình bày một định nghĩa yếu hơn về an toàn, được gọi là an toàn “ngữ nghĩa” Trong thiết kế này khái niệm an toàn cũng được định nghĩa giống như ở đây, trừ một điểm là nói chung kẻ tấn công không được phép thực hiện bất kỳ truy vấn tiên tri giải mã nào.
B.4.1. Che giấu độ dài bản rõ
Lưu ý rằng trong cuộc tấn công, đòi hỏi kẻ tấn công phải chuyển cho tiên tri mã hóa hai bản rõ đích có cùng độ dài. Hạn chế này lên kẻ tấn công phản ánh một sự thật là, không thể che giấu kẻ tấn công độ dài của bản rõ được mã hóa - đối với nhiều hệ mật mã thì độ dài bản rõ được thấy rõ từ độ dài bản mã. Nói chung là điều này được áp dụng trong ứng dụng mật mã để đảm bảo là độ dài bản rõ không để lộ thông tin nhạy cảm.
Với mật mã độ dài bản rõ bị giới hạn, khái niệm an toàn cũng giống như trong các trường hợp thông thường, trừ một điểm là không yêu cầu kẻ tấn công trình các bản rõ đích có cùng độ dài cho tiên tri mã hóa. Điều này phản ánh một sự thật là những lược đồ này có thể che giấu độ dài của bản rõ đối với kẻ tấn công.
Với mật mã phi đối xứng độ dài bản rõ cố định, thì vấn đề trên không bị phát sinh.
B.4.2. Tính dễ bị uốn nhẹ: Khái niệm yếu hơn một ít về an toàn
Định nghĩa tính an toàn trên đây có thể coi là mạnh đến mức không cần thiết. Ví dụ, lấy một mật mã phi đối xứng AC thỏa mã định nghĩa trên và thay đổi nó để nhận được mật mã mới AC’ như sau: AC' cũng giống như AC, chỉ trừ một điểm là một bộ tám ngẫu nhiên được gắn vào bản mã sau khi mã hóa và loại bộ tám bổ sung đó trước khi giải, về phương diện kỹ thuật, AC’ không thỏa mãn định nghĩa trên đối với tính an toàn bản mã lựa chọn thích hợp mà dường như điều này là phi trực quan. Thật vậy, mặc dù về mặt kỹ thuật AC’ là “dễ bị uốn”, nhưng chỉ dễ bị uốn theo một kiểu “nhẹ": có thể tạo ra các bản mã khác nhau của cùng một bản rõ, và các bản mã khác nhau đó đều dễ dàng bị nhận dạng là bản thay thế của một bản rõ.
Điều này mô tả khái niệm hình thức về tính an toàn, phản ánh chính xác khái niệm trực giác của "tính dễ uốn nhẹ".
Đối với mật mã phi đối xứng cụ thể AC, hàm giá trị 0/1, thời gian đa thức Equiv, được gọi là thuộc tính tương đương (equivalence predicate) cho AC, nếu với xác suất trội, đầu ra của AC.KeyGen là cặp (PK,pk) sao cho với nhãn bất kỳ L và hai bản mã bất kỳ C và C', ta có:
Equiv(PK,L,C,C') = 1 suy ra AC.Decrypt(pk,L,C) = AC. Decrypt(pk,L,C').
Mã đối xứng AC được gọi là dễ uốn nhẹ, nếu tồn tại thuộc tính tương đương Equiv và nếu nó thỏa mãn định nghĩa an toàn ở trên về tính an toàn chống lại tấn công chọn bản mã thích hợp, nhưng với cải biên sau đây trong cuộc chơi tấn công: khi kẻ tấn công trình cặp nhãn/bản mã (L,C') cho tiên tri giải mã ở bước 4, thì thay vì yêu cầu cặp (L,C) ≠ (L*,C*), đòi hỏi L* ≠ L hoặc Equiv(PK,L,C,C*) = 0. Đối với kẻ tấn công A, ưu thế của nó trong cấu trúc này ký hiệu bằng Adv'AC(A).
B.5. Các cơ chế bọc khóa
Điều này mô tả thuộc tính an toàn cơ bản đòi hỏi đối với cơ chế bọc khóa.
Xét cơ chế bọc khóa KEM được định nghĩa trong Điều 8.1.
Xét kịch bản tấn công “chọn bản mã thích hợp" sau:
Bước 1: Chạy thuật toán tạo khóa, tạo ra khóa công khai và khóa riêng. Kẻ tấn công, hiển nhiên, biết được khóa công khai nhưng không biết khóa riêng.
Bước 2: Kẻ tấn công đưa ra một loạt câu truy vấn cho tiên tri giải mã. Mỗi câu truy vấn là bản mã C0, được giải mã bởi tiên tri giải mã, sử dụng khóa riêng. Kết quả giải mã được trao cho kẻ tấn công, hơn nữa nếu thuật toán thất bại thì thông tin này được trao cho kẻ tấn công và tấn công được tiếp tục. Kẻ tấn công tự do kiến thiết các bản mã này theo một cách tùy ý - không cần sử dụng thuật toán mã hóa để tính toán chúng.
Bước 3: Kẻ tấn công gọi tiên tri mã hóa bằng cách cung cấp tùy chọn mật mã nào đó, nếu lược đồ hỗ trợ điều này, Tiên tri mã hóa thực hiện như sau:
a) Chạy thuật toán mã hóa, tạo ra cặp (K*,![]() ).
).
b) Tạo ra xâu bộ tám ngẫu nhiên ![]() độ dài KEM.KeyLen.
độ dài KEM.KeyLen.
c) Chọn ngẫu nhiên b Î {0,1}.
d) Nếu b = 0, đưa ra (K*,![]() ); ngược lại đưa ra là (
); ngược lại đưa ra là (![]() ,
,![]() ).
).
Bước 4: Kẻ tấn công tiếp tục chuyển bản mã C0 cho tiên tri giải mã với điều kiện ràng buộc C0 ≠ ![]() .
.
Bước 5: Kẻ tấn công đưa ra ![]() Î {0,1} và dừng lại.
Î {0,1} và dừng lại.
Ưu thế của A được định nghĩa bằng giá trị ![]() |. Với kẻ tấn công A, và cơ chế bọc khóa KEM, ưu thế của A được ký hiệu là AdvKEM(A). Nếu kẻ tấn công thực hiện trong thời gian t, thực hiện nhiều nhất là q truy vấn tiên tri giải mã, khi đó A được gọi là kẻ tấn công - KEM[t,q].
|. Với kẻ tấn công A, và cơ chế bọc khóa KEM, ưu thế của A được ký hiệu là AdvKEM(A). Nếu kẻ tấn công thực hiện trong thời gian t, thực hiện nhiều nhất là q truy vấn tiên tri giải mã, khi đó A được gọi là kẻ tấn công - KEM[t,q].
Tính an toàn có nghĩa là ưu thế đối với tất cả kẻ tấn công hiệu quả là không đáng kể.
B.5.1. Tính dễ uốn nhẹ
Điều này định nghĩa khái niệm tính dễ uốn nhẹ cho cơ chế bọc khóa tương ứng với khái niệm tính dễ uốn đối với mã phi đối xứng, như trong Phụ lục B.4.2.
Đối với cơ chế bọc khóa cụ thể KEM, hàm giá trị 0/1, thời gian đa thức Equiv được gọi là thuộc tính tương đương đối với KEM, nếu với xác suất trội, đầu ra của KEM.KeyGen là cặp (PK, pk) sao cho với hai bản mã bất kỳ C0 và ![]() , ta có:
, ta có:
Equiv(PK,C0,![]() ) = 1 suy ra KEM.Decrypt(pk,C0) = KEM.Decrypt(pk,
) = 1 suy ra KEM.Decrypt(pk,C0) = KEM.Decrypt(pk,![]() ).
).
Cơ chế bọc khóa KEM được gọi là dễ uốn nhẹ, nếu tồn tại thuộc tính tương đương Equiv và nếu nó thỏa mãn định nghĩa an toàn ở trên về tính an toàn chống lại tấn công chọn bản mã thích hợp, nhưng với thay đổi sau đây trong cuộc tấn công: khi kẻ tấn công gửi cặp bản mã C0 cho tiên tri giải mã ở bước 4, thì yêu cầu C0 ≠ ![]() được thay bởi Equiv(PK,C0,
được thay bởi Equiv(PK,C0,![]() ) = 0. Đối với kẻ tấn công A, lợi thế của nó trong cấu trúc này ký hiệu bằng Adv'KEM(A).
) = 0. Đối với kẻ tấn công A, lợi thế của nó trong cấu trúc này ký hiệu bằng Adv'KEM(A).
B.6. Các cơ chế bọc dữ liệu
Điều này mô tả thuộc tính an toàn cơ bản được yêu cầu đối với cơ chế bọc dữ liệu.
Xét cơ chế bọc khóa DEM được định nghĩa trong Điều 8.2.
Xét kịch bản tấn công sau. Kẻ tấn công tạo ra hai bản rõ (hai xâu bộ tám) M0,M1 có độ dài bằng nhau và nhãn L*. Khóa bí mật K được tạo một cách ngẫu nhiên. Chọn ngẫu nhiên bit b và Mb được mã hóa bằng khóa bí mật K. Bản mã thu được ![]() được trao cho kẻ tấn công. Tiếp đó kẻ tấn công đưa ra một loạt các truy vấn cho tiên tri giải mã: mỗi truy vấn là một cặp nhãn/bản mã (L,C1) ≠ (L*,
được trao cho kẻ tấn công. Tiếp đó kẻ tấn công đưa ra một loạt các truy vấn cho tiên tri giải mã: mỗi truy vấn là một cặp nhãn/bản mã (L,C1) ≠ (L*,![]() ) và tiên tri giải mã tương ứng với bản giải mã của C1 với nhãn L và khóa K. Kẻ tấn công phỏng đoán giá trị
) và tiên tri giải mã tương ứng với bản giải mã của C1 với nhãn L và khóa K. Kẻ tấn công phỏng đoán giá trị ![]() của b.
của b.
Ưu thế của kẻ tấn công được định nghĩa bằng ![]()
Giả sử A là kẻ tấn công A và DEM là cơ chế bọc dữ liệu. Ưu thế của A được ký hiệu là AdvDEM(A). Nếu kẻ tấn công chạy trong thời gian t, thực hiện nhiều nhất là q truy vấn tiên tri, tất cả các bản mã là đầu ra từ mã hóa tiên tri và đầu vào của giải mã tiên tri có độ dài lớn nhất là l bộ tám và các nhãn đầu vào của mã hóa và giải mã tiên tri lớn nhất là l', khi đó A được gọi là kẻ tấn công -DEM[t,q,l,l'].
Tính an toàn có nghĩa là ưu thế trên không đáng kể đối bất kỳ kẻ tấn công hiệu quả nào.
B.6.1. An toàn DEM1, DEM2 và DEM3
Điều khoản này xem xét tính an toàn của các cơ chế bọc dữ liệu DEM1 (xem Điều 9.1), DEM2 (xem Điều 9.2), và DEM3 (xem Điều 9.3).
Xét cơ chế DEM1. Lược đồ này được tham số hóa bởi mã đối xứng SC và thuật toán xác thực thông báo MA. Có thể chỉ ra rằng nếu SC thỏa mãn định nghĩa an toàn tại Phụ lục B.3 và MA thỏa mãn định nghĩa an toàn tại Phụ lục B.1, khi đó DEM1 thỏa mãn định nghĩa an toàn tại Phụ lục B.6.
Cụ thể hơn, với bất kỳ kẻ tấn công A - DEM1[t,q,l,l'] ta có:
AdvDEM1(A) ≤ AdvSC(A1) + AdvMA(A2),
ở đây,
- A1 là kẻ tấn công [t1,l''] với t1 ≈ t,
- A2 là kẻ tấn công MA[t2,q,l''] với t2 ≈ t,và
- l" = l - MA.MACLen.
Tương tự, với bất kỳ tấn công A - DEM2[t,q,l,l''], ở đây cần thỏa mãn l' = DEM2.LabelLen, chúng ta có
AdvDEM2(A) ≤ AdvSC(A1) + AdvMA(A2),
ở đây
- A1 là kẻ tấn công SC[t1,l''], với t1 ≈ t,
- A2 là kẻ tấn công MA[t2,q,l'' + l'] với t2 ≈ t, và
- l'' = I - MA.MACLen.
Tương tự, với bất kỳ kẻ địch A - DEM3[t,q,l,l'], ở đây cần thỏa mãn l = DEM3.MsgLen + MA.MACLen, chúng ta có
AdvDEM3(A) ≤ AdvMA(A2),
Ở đây
- A2 là kẻ tấn công MA[t2,q,DEM3.MsgLen + l'], với t2 ≈ t.
Dễ dàng xác lập các giới hạn này từ định nghĩa. Xem, chẳng hạn [14], để chứng minh cho DEM2 với LabelLen = 0. Chứng minh cho những trường hợp khác có thể tiến hành theo những mạch suy luận tương tự như trong [14].
B.7. An toàn của HC
Điều khoản này mô tả độ an toàn của mật mã lai ghép HC, được quy định tại điều 8.3. Lược đồ này được tham số hóa liên quan tới cơ chế bọc khóa KEM và cơ chế bọc dữ liệu DEM.
Có thể chỉ ra rằng, nếu KEM thỏa mãn định nghĩa tính an toàn tại phụ lục B.5 và DEM thỏa mãn định nghĩa an toàn tại Phụ lục B.6, khi đó HC thỏa mãn định nghĩa tại Điều B.4.
Cụ thể hơn, với mọi kẻ tấn công A - HC[t,q,l,l’], ta có
AdvHC(A) ≤ 2.AdvDEM(A1) + AdvKEM(A2).
Ở đây,
- A1 là kẻ tấn công [t1,q], với t1 ≈ t,
- A2 là kẻ tấn công DEM[t2,q,l,l'] với t2 ≈ t, và
Bất đẳng thức trên không tính đến khả năng KEM.KeyGen đưa ra cặp khóa “tồi" (ví dụ một trong những cặp như thế là thuật toán giải mã không vận hành như thuật toán nghịch đảo của thuật toán mã hóa) với xác suất khác không. Trong trường hợp này, đơn giản là cần bổ sung xác suất này (được coi là không đáng kể) vào bên phải của bất đẳng thức trên.
Giới hạn này dễ dàng thiết lập từ các định nghĩa. Xem, chẳng hạn trong [14], chứng minh chi tiết trong trường hợp không có nhãn. Chứng minh trong trường hợp có nhãn có thể tiến hành theo các mạch suy luận tương tự như trong [14]. Nếu KEM là dễ uốn nhẹ (xem Phụ lục B.5.1), thì dễ dàng chỉ ra rằng HC cũng dễ uốn nhẹ (xem Phụ lục B.4.2) với cùng một giới hạn an toàn như trên.
B.8. Các giả thuyết về tính khó liên quan đến các nhóm cụ thể
Điều này xác định một số giả thuyết về tính khó liên quan đến các nhóm cụ thể.
Giả sử G = ![]() là nhóm cụ thể được định nghĩa ở Điều 10.1.
là nhóm cụ thể được định nghĩa ở Điều 10.1.
B.8.1. Bài toán tính toán Diffie-Hellman.
Bài toán tính toán Diffie-Hellman (CDH) đối với G phát biểu như sau. Cho đầu vào (xg, yg) với x, y Î [0,…,m) Hãy tính xy.g, giả thiết đầu vào ngẫu nhiên, tức x và y được chọn ngẫu nhiên từ tập hợp [0,…,m).
Giả thiết CDH là giả thiết rằng bài toán tính toán Diffie-Hellman là bài toán khó.
Lưu ý rằng rất khó, thậm chí, nhận dạng lời giải đúng cho bài toán CDH (đây được gọi là bài toán quyết định Diffie-Hellman-xem phần tiếp theo dưới đây). Trong khi phân tích các hệ mật, các dạng thuật toán để giải bài toán CDH mà phần lớn là phát sinh một cách tự nhiên là những thuật toán cho ra một danh sách các lời giải có thể đối với trường hợp đã cho của bài toán CDH. Với thuật toán A bất kỳ giải bài toán CDH, đầu ra của nó là một danh sách các phần tử nhóm, ta ký hiệu AdvCDHG(A) là xác suất để danh sách đó chứa lời giải đúng đối với đầu vào bài toán. Nếu A chạy trong thời gian t và tạo ra được danh sách nhiều nhất là l phần tử nhóm, thì A được gọi là kẻ tấn công CDHG(t,l).
Trong [32] đã chỉ ra, làm thế nào để, kẻ tấn công CDHG(t,l) với e =AdvCDHG(A) và giá trị δ cho trước, biến đổi thành kẻ tấn công A’ - CDHG[t',1], sao cho AdvCDHG(A’) = 1-δ và sao cho t' tương đương 0(t ∙ Î-1 log(1/δ)) cộng với thời gian thực hiện số các phép toán nhóm là:
0(Î-1l log(1/δ) logm + (logm)2)
B.8.2. Bài toán quyết định Diffie-Hellman
Bài toán quyết định Diffie-Hellman (DDH) đối với G được phát biểu như sau:
Xác định hai phân bố:
Phân bố R gồm bộ ba (xg, yg, zg), ở đây x, y, z được chọn ngẫu nhiên từ tập hợp [0,...,m). Giả sử XR là biến ngẫu nhiên được lấy mẫu từ phân bố này.
Phân bố D bao gồm bộ ba (xg, yg, zg), ở đây x, y được chọn ngẫu nhiên từ tập hợp [0,...,m), còn z = xy mod m. Ký hiệu XD là biến ngẫu nhiên với mẫu được lấy từ phân bố D.
Bài toán quyết định Diffie-Hellman là phân biệt hai phân bố nói trên (R và D)
Với thuật toán A mà đầu ra hoặc là 0 hoặc là 1, “Ưu thế DDH“ của nó được định nghĩa bằng
AdvCDHG(A) = |Pr[A(XR) = 1] - Pr[A(XD) = 1]|.
Nếu A chạy trong thời gian t thì A được gọi là kẻ tấn công DDHG[t].
Giả thiết DDH là: Ưu thế này là không đáng kể đối với tất cả các thuật toán hiệu quả.
Tham khảo thêm [10, 25, 26] về DDH và các vấn đề liên quan.
B.8.3. Bài toán Gap-CDH
Bài toán Gap-CDH là bài toán giải bài toán CDH với sự hỗ trợ của tiên tri cho bài toán DDH. Trong trường hợp này, vì thuật toán cho bài toán này sử dụng tiên tri DDH, có thể giả thiết là đầu ra của thuật toán là phần tử nhóm đơn lẻ, chứ không phải một danh sách các phần tử nhóm.
Giả thiết rằng bài toán Gap-CDH là bài toán khó.
Với bất kỳ thuật toán "tiên tri” A, AdvGapCDHG(A) được định nghĩa là xác suất để cho ra lời giải đúng cho trường hợp ngẫu nhiên của bài toán CDH, sử dụng tiên tri đối với G. Nếu A chạy trong thời gian nhiều nhất là t, và thực hiện nhiều nhất q truy vấn đối với DDH-tiên tri, thì A được gọi là kẻ tấn công GapCDHG[t,q].
Tham khảo [29] để biết thêm chi tiết về giả thiết này.
B.9. Tính an toàn của ECIES-KEM
Điều này xem xét tính an toàn của cơ chế bọc khóa ECIES - KEM được định nghĩa ở Điều 10.2.
Lược đồ này được tham số hóa theo thuật ngữ của nhóm cụ thể G (xem Điều 10.1) và hàm dẫn xuất khóa KDF (xem Điều 6.2).
Có thể chứng minh lược đồ này là an toàn theo mô hình tiên tri ngẫu nhiên, nơi KDF được mô hình hóa như tiên tri ngẫu nhiên, với giả thiết là bài toán Gap-CDH là bài toán khó.
Cụ thể hơn, giả sử rằng các tham số hệ thống của ECIES-KEM được chọn sao cho SingleHashMode = 0 và
CheckMode + CofactorMode + OldCofactorMode > 0.
Khi đó nếu A là kẻ tấn công ECIES - KEM[t,q] và thực hiện nhiều nhất q’ truy vấn tiên tri ngẫu nhiên, khi đó ta có
AdVECIES-KEM (4) = O(AdvGapCDHG(A')),
ở đấy,
- A' là kẻ tấn công GapCDHG(t',O(q'),t’ ≈ t.
Giới hạn này về cơ bản đã được chứng minh trong [14], ít nhất cũng cho trường hợp khi CheckMode = 1 và các phần tử nhóm có mã duy nhất. Các trường hợp khác có thể chứng minh bằng lập luận tương tự.
Giả sử các tham số hệ thống của ECIES - KEM được chọn sao cho SingleHashMode = 1 và
CheckMode + CofactorMode + OldCofactorMode > 0.
Trong trường hợp này ECIES - KEM sẽ không còn an toàn chống lại tấn công chọn bản mã, nhưng lại dễ uốn nhẹ (tham khảo Phụ lục B.5.1). Nếu khi đó nếu A là kẻ tấn công ECIES - KEM[t,q] và thực hiện nhiều nhất q’ truy vấn tiên tri ngẫu nhiên, khi đó ta có
Adv'ECIES-KEM (A) = O(AdvGapCDHG(A’)),
ở đây,
- A’ là kẻ tấn công GapCDHG(t',O(q.q'), t' ≈ t.
Ngoài ra, chỉ thỏa mãn định nghĩa yếu về an toàn, thì phép quy dẫn này sẽ không chặt chẽ như trong trường hợp ở đó SingleHashMode = 0. Đồng thời chất lượng của phép quy dẫn bị suy giảm, thậm chí còn giảm hơn với SingleHashMode = 1, khi xem xét mô hình đa bản rõ được định nghĩa một cách hình thức trong [3], ngược lại phép quy dẫn không suy giảm đáng kể khi SingleHashMode = 0.
Nếu
CheckMode + CofactorMode + OldCofactorMode = 0,
khi đó, trong cả hai ước lượng trên, thuật ngữ AdvGapCDHG(A'), cần được thay thế bởi v.AdvGapCDHG(A').
Bởi vậy, sự lựa chọn tham số hệ thống này chỉ nên sử dụng khi v rất bé.
Thay vì phân tích ECIES - KEM theo thuật ngữ của giả thiết Gap-CDH trong mô hình tiên tri ngẫu nhiên, có thể phân tích nó mà không cần sử dụng các tiên tri ngẫu nhiên, nhưng với giả thiết rất cụ thể và không chuẩn tắc. Tham khảo tại [1, 2] để biết thêm chi tiết.
B.10. Tính an toàn của PSEC-KEM
Điều này xem xét tính an toàn của cơ chế bọc khóa PSEC - KEM được định nghĩa tại Điều 10.3.
Lược đồ này được tham số hóa bằng thuật ngữ của nhóm cụ thể G (xem Điều 10.1) và hàm dẫn xuất khóa KDF (Điều 6.2).
Có thể chứng minh sự an toàn của lược đồ này theo mô hình tiên tri ngẫu nhiên, coi KDF như tiên tri ngẫu nhiên và giả thiết bài toán CDH là bài toán khó.
Cụ thể hơn, với giá trị cho trước của tham số hệ thống SeedLen và với A-kẻ tấn công PSEC - KEM[t,q] thực hiện nhiều nhất q' truy vấn ngẫu nhiên, ta có
AdvPSEC.KEM(A) = O(AdvCDHG(A') + (q+ q')(m-1 + 2-SeedLen)),
ở đây A' là kẻ tấn công AdvCDHG[t',O(q + q')], t' ≈ t.
Giới hạn này được chứng minh trong [41].
Đồng thời tính an toàn cũng không bị suy giảm đáng kể trong mô hình đa bản rõ được định nghĩa trong [10].
B.11. Tính an toàn của ACE-KEM
Điều này xem xét tính an toàn của cơ chế bọc khóa ACE-KEM, được định nghĩa trong 10.4.
Lược đồ này được tham số hóa bằng thuật ngữ của nhóm cụ thể G (xem Điều 10.1), hàm dẫn xuất khóa KDF(xem Điều 6.2) và hàm băm hash (Điều 6.1).
Lược đồ này có thể được chứng minh là an toàn, với giả thiết bài toán DDH là bài toán khó-cần nhấn mạnh là chứng minh về tính an toàn này không có trong mô hình tiên tri ngẫu nhiên. Thay vì điều này, một số giả thiết cụ thể và tương đối chuẩn tắc đã được đưa ra về hàm dẫn xuất khóa và hàm băm.
Cụ thể hơn, với bất kỳ kẻ tấn công A, ACE - KEM [t,q], ta có
AdvACE-KEM (A) = O (AdvDDHG(A1) + AdvHash(A2) + AdvKDF(A3) + q.m-1),
ở đây:
- A1, A2, A3 là những kẻ tấn công, thực hiện với lượng thời gian như A
- AdvHaSh(A2) là ký hiệu xác suất mà kẻ tấn công A2, với mã cho trước EU1* và EU2* của hai phần tử độc lập, ngẫu nhiên thuộc …….., có thể tìm thấy mã EU1, và EU2 của các phần tử thuộc ……., sao cho (EU1, EU2) ≠ (EU1*, EU2*), nhưng
Hash.eval (EU1 || EU2) = Hash.eval (EU1* || EU2*).
Nếu nhóm hỗ trợ đa mã hóa, thì kẻ tấn công có thể chọn định dạng theo ý muốn, khi EU1* và EU2* được tạo ra. Hơn nữa kẻ tấn công có thể chọn sử dụng các định dạng như nhau hoặc khác nhau trong hai lựa chọn của nó là EU1 và EU2. Tuy nhiên EU1* và EU2* phải là các mã hóa bền vững, và EU1 và EU2 cũng sở hữu các tính chất đó.
Nếu CofactorMode = 1, thì kẻ tấn công có thể chọn EU1 làm mã của phần tử thuộc ![]() mà không nhất thiết thuộc
mà không nhất thiết thuộc ![]()
Lưu ý rằng bài toán này là bài toán xung đột tiền ảnh thứ hai, bài toán này nói chung là bài toán khó giải hơn nhiều so với bài toán tìm một cặp bất kỳ đầu vào xung đột.
- AdvKDF(A3) ký hiệu ưu thế của A3 trong việc phân biệt giữa hai phân bố sau. Giả sử u1 và ![]() là các phần tử độc lập, ngẫu nhiên trong
là các phần tử độc lập, ngẫu nhiên trong ![]() và giả sử EU1 là mã của u1. Giả sử R là xâu các bộ tám ngẫu nhiên độ dài KeyLen. Phân bố thứ nhất là (R, EU1), và phân bố thứ hai là (KDF(EU1 || e'(
và giả sử EU1 là mã của u1. Giả sử R là xâu các bộ tám ngẫu nhiên độ dài KeyLen. Phân bố thứ nhất là (R, EU1), và phân bố thứ hai là (KDF(EU1 || e'(![]() ),KeyLen),EU1).
),KeyLen),EU1).
Độc giả có thể tham khảo [14] để xem chứng minh chi tiết cho trường hợp CofactorMode = 0 và các phần tử nhóm có mã duy nhất. Dễ dàng chuyển chứng minh sang các trường hợp khác, sử dụng yếu tố là thuật toán giải mã kiểm tra các mã hóa bền vững.
Trong [14] đồng thời cũng chỉ ra rằng, độ an toàn của ACE - KEM không kém hơn ECIES - KEM, tức là với bất kỳ kẻ tấn công - ACE - KEM [t,q] A tồn tại một kẻ tấn công - ECIES - KEM [t',q] A' với t’ ≈ t và AdvECIES-KEM(A') ≈ AdvACE-KEM(A). Chứng minh trong [14] chỉ cho trường hợp CofactorMode = 0 và các phần tử của nhóm có mã hóa duy nhất. Chứng minh này dễ dàng thích hợp để xử lý các trường hợp khác, một lần nữa làm cho việc sử dụng thực tế là kiểm tra thuật toán giải mã cho mã hóa thích hợp.
Trong [14] đồng thời cũng chỉ ra rằng, nếu coi KDF như tiên tri ngẫu nhiên, thì tính an toàn của ACE - KEM có thể được chứng minh dựa trên giả thiết CDH. Tuy nhiên, phép quy dẫn này về tính an toàn cũng không hoàn toàn chặt chẽ. Chứng minh trong [14] chỉ để cho trường hợp CofactorMode = 0 và các phần tử nhóm có mã duy nhất. Chứng minh này dễ dàng chuyển sang cho các trường hợp khác.
Như đã chỉ ra trong Điều 10.4.4, nên lưu ý đến việc thực thi ACE - KEM.Decrypt. Đặc biệt, việc thực thi ACE - KEM.Decrypt không nên để lộ nguyên nhân của sai sót trong bước g. Nếu kẻ tấn công có thể thu được thông tin từ tiên tri giải mã, việc chứng minh tính an toàn trong giả thiết DDH sẽ không còn giá trị nữa. Tuy nhiên, thậm chí nếu thông tin này tiếp cận được, thì hiện chưa biết tấn công nào vào lược đồ này, và hơn nữa lược đồ vẫn không kém an toàn hơn so với ECIES-KEM.
B.12. Bài toán ngược RSA
Điều này xem xét bài toán ngược RSA.
Giả sử RSAKeyGen là thuật toán tạo khóa RSA (xem Điều 11.1).
Bài toán ngược RSA phát biểu như sau: Cho đầu vào n và e của thuật toán RSAKeyGen(), cho x Î [0 ...n) hãy tính y sao cho ye ≡ x (mod n). Với thuật toán A bất kỳ và thuật toán tạo khóa cho trước RSAKeyGen, AdvRSAKeyCen(A) ký hiệu xác suất của A giải thành công bài toán ngược nói trên. Nếu A chạy trong lượng thời gian nhiều nhất t, thì được gọi là kẻ tấn công RSAKeyGen[t].
Giả thiết RSA đối với RSAKeyGen là giả thiết: AdvRSAKeyGen(A) không đáng kể đối với bất kỳ thuật toán hiệu quả A nào.
B.13. Tính an toàn của RSAES
Điều này xem xét tính an toàn của mật mã có độ dài bản rõ hạn chế RSAES, được định nghĩa trong Điều 11.4.
Trong [8] đã phân tích một cài đặt tổng quát hơn, trong đó (phương án thứ yếu của) cơ chế mã hóa REM1 (được định nghĩa tại Điều 11.3.2) được áp dụng cho phép “hoán vị cửa sập một chiều” tổng quát, chứ không chỉ cho hàm RSA một chiều cụ thể. Việc phân tích được tiến hành theo mô hình tiên tri ngẫu nhiên, ở đấy hàm dẫn xuất khóa và hàm băm được mô hình như những tiên tri.
Trong [8] cũng đã chứng minh rằng lược đồ thu được thỏa mãn một tính chất kỹ thuật, được gọi là “nhận thức bản rõ' (plaintext awareness), với giả thiết rằng phép hoán vị cơ sở thực sự là hàm một phía. Ngoài ra, như đã chỉ ra trong [33], việc nhận biết bản rõ không suy ra được tính an toàn chống lại tấn công chọn bản mã - nó chỉ suy ra khái niệm yếu hơn về an toàn, đó là an toàn chống lại tấn công “thời gian ăn bữa trưa” (xem Phụ lục B.4). Hơn nữa, trong [33] cũng đã chứng minh rằng nói chung REM1 không tạo ra mật mã an toàn chống lại tấn công chọn bản mã, nếu phép hoán vị cơ sở là tùy ý. Kết quả phủ định này không suy ra rằng RSAES là không an toàn chống lại tấn công chọn bản mã - chỉ suy ra rằng phân tích trong [8] không đạt được điều này.
Trong [33], đã chỉ ra rằng RSAES là an toàn, nếu số mũ mã hóa e là rất bé (ví dụ e = 3). Kết quả này đã được tổng quát trong [20] cho số mũ mã hóa tổng quát. Tuy nhiên có thể chỉ ra rằng phép quy dẫn của tính an toàn trong [20] là rất không chặt chẽ - thật vậy, nói chung chưa có thể nói gì về tính an toàn của RSAES đối với modulo RSA kích thước tới hàng ngàn bit. Phép quy dẫn an toàn trong [33] cho số mũ mã hóa nhỏ là tốt hơn đáng kể, nhưng vẫn không hoàn toàn chặt chẽ như đòi hỏi.
Như đã chỉ ra trong Điều 11.3.2.3, cần quan tâm đến vấn đề thực thi RSAES. Đặc biệt là việc thực thi REM1.Decode không nên để lộ nguyên nhân sai sót tại bước thứ k; Nếu kẻ tấn công có thể thu được thông tin này từ tiên tri giải mã, thì lược đồ có thể dễ dàng bị phá, như mô tả trong [24].
B.14. Tính an toàn của RSA-KEM
Điều này xem xét tính an toàn của cơ chế bọc khóa RSA-KEM, được định nghĩa trong Điều 11.5.
Có thể chứng minh tính an toàn của lược đồ này theo mô hình tiên tri ngẫu nhiên, nơi các tham số hệ thống KDF được mô hình hóa dưới dạng tiên tri ngẫu nhiên và giả thiết bài toán ngược RSA là bài toán khó.
Cụ thể hơn, với bất kỳ thuật toán tạo khóa RSAKeyGen, sao cho đầu ra (n,e,d) luôn luôn thỏa mãn điều kiện n ≥ nBound, và với mỗi kẻ tấn công A, RSA - KEM[t,q] ta có
AdvRSA-KEM (A) ≤ AdvRSAKeyGen (A') + q/nBound.
ở đây,
- A' là kẻ tấn công RSAKeyGen[t'] với t' ≈ t.
Bất đẳng thức này không tính đến khả năng của biến cố RSAKeyGen tạo ra khóa RSA “tồi" với xác suất khác không. Trong trường hợp này, đơn giản là cần bổ sung xác suất này (giả thiết là không đáng kể) vào vế phải của bất đẳng thức trên.
Xem chứng minh tại [34].
Phép quy dẫn này hoàn toàn chặt chẽ, khác với phép quy dẫn cho RSAES được thảo luận ở trên trong Phụ lục B.13. Ngoài ra, trong mô hình đa bản rõ được định nghĩa trong [3], tính an toàn của RSA-KEM nói chung không suy giảm do tính tự quy dẫn ngẫu nhiên của bài toán ngược RSA. Ngược lại, tính an toàn của RSAES suy giảm một cách tuyến tính theo số lượng bản rõ, vì không may là tính chất tự quy dẫn ngẫu nhiên không thể khai thác được trong bối cảnh này.
Đồng thời, không giống như RSAES, không có cảm giác là RSA-KEM dễ bị tổn thương đối với các tấn công “thực thi", như tấn công trong [24].
B.15. Tính an toàn của HIME(R)
Có thể chỉ ra rằng theo mô hình tiên tri ngẫu nhiên, nơi hàm Hash và KDF trong HEM1 được mô hình hóa dưới dạng tiên tri ngẫu nhiên, rằng HIME(R) là an toàn chống lại tấn công chọn bản rõ phù hợp, với giả thiết là bằng tính toán để không thể phân tích số nguyên ở dạng mà ra bởi thuật toán HIMEKeyGen. Để xem chi tiết, tham khảo [29, 35] - lưu ý là [35] đã chỉnh sửa một số sai sót trong [29].
PHỤ LỤC C
(Tham khảo)
CÁC VÉC TƠ KIỂM TRA
Phụ lục này đưa ra các véc tơ kiểm tra cho lược đồ mã hóa được đặc tả trong phần này của tiêu chuẩn ISO/IEC 18033.
Đối với các cơ chế bọc khóa dựa trên ELGamal, nhóm “Modp” là một nhóm con của ![]() với số nguyên tố p cho trước; nhóm “ECModp” là các đường cong elliptic trên Zp, đôi khi được gọi là “P192" trong các tiêu chuẩn khác; nhóm “ECGF2" là các đường cong elliptic trên trường hữu hạn gồm có 2163 phần tử, đôi khi được gọi là "B163“ trong các tiêu chuẩn khác (các phần tử trong trường được mô tả với quan hệ của đa thức cơ sở cho đa thức bất khả quy p đã cho).
với số nguyên tố p cho trước; nhóm “ECModp” là các đường cong elliptic trên Zp, đôi khi được gọi là “P192" trong các tiêu chuẩn khác; nhóm “ECGF2" là các đường cong elliptic trên trường hữu hạn gồm có 2163 phần tử, đôi khi được gọi là "B163“ trong các tiêu chuẩn khác (các phần tử trong trường được mô tả với quan hệ của đa thức cơ sở cho đa thức bất khả quy p đã cho).
C.1. Véc tơ kiểm tra cho DEM1
C.1.1. Véc tơ kiểm tra

C.1.2 Véc tơ kiểm tra
![]()

C.2. Véc tơ kiểm tra cho ECIES-KEM
C.2.1. Véc tơ kiểm tra


C.2.2. Véc tơ kiểm tra


C.2.3. Véc tơ kiểm tra ECIES-KEM


C.2.4. Véc tơ kiểm tra ECIES-KEM


C.2.5. Véc tơ kiểm tra ECIES-KEM
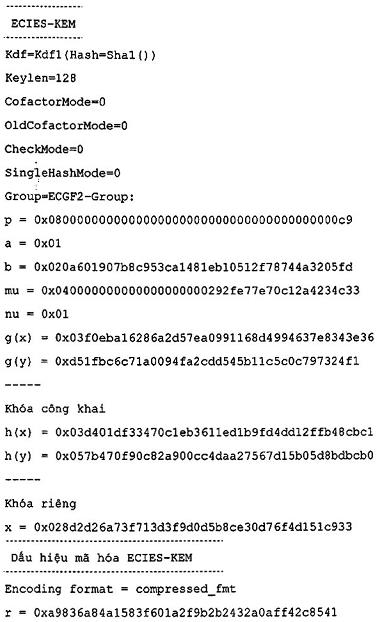

C.3. Véc tơ kiểm tra cho PSEC-KEM
C.3.1. Véc tơ kiểm tra


C.3.2. Véc tơ kiểm tra


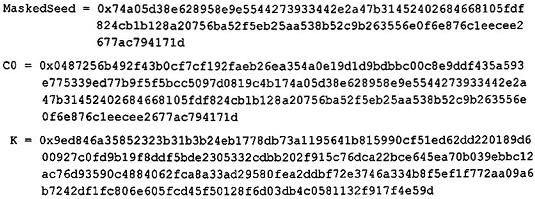
C.3.3. Véc tơ kiểm tra


C.3.4 Véc tơ kiểm tra



C.3.5. Véc tơ kiểm tra


C.4. Véc tơ kiểm tra cho ACE-KEM
C.4.1. Véc tơ kiểm tra



C.4.2. Véc tơ kiểm tra



C.4.3. Véc tơ kiểm tra ACE-KEM


C.4.4. Véc tơ kiểm tra



C.4.5. Véc tơ kiểm tra



C.5. Véc tơ kiểm tra cho RSAES
C.5.1. Véc tơ kiểm tra


C.5.2. Véc tơ kiểm tra
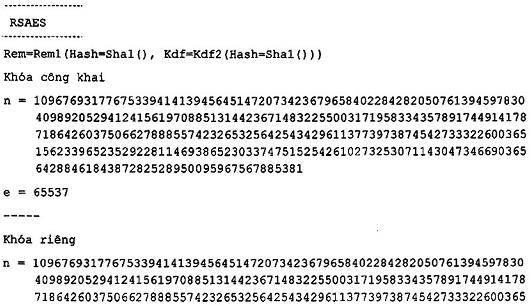

C.5.3. Véc tơ kiểm tra


C.5.4. Véc tơ kiểm tra


C.6. Véc tơ kiểm tra cho RSA-KEM
C.6.1. Véc tơ kiểm tra


C.6.2. Véc tơ kiểm tra


C.6.3. Véc tơ kiểm tra


C.6.4. Véc tơ kiểm tra

C.7. Véc tơ kiểm tra cho HC
Kết hợp mỗi KEM với DEM là khá đơn giản, nhưng liệt kê tất cả các kết hợp khác nhau có thể khó và mất nhiều thời gian. Chúng tôi cung cấp ở đây chỉ là một vector thử nghiệm như là một minh họa.
C.7.1. Véc tơ kiểm tra



C.8. Véc tơ kiểm tra cho HIME(R)
C.8.1. Véc tơ kiểm tra
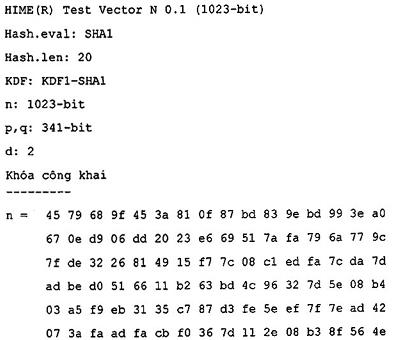



C.8.2. Véc tơ kiểm tra
Véc tơ kiểm tra HIME (R). No.2 (1023-bit)
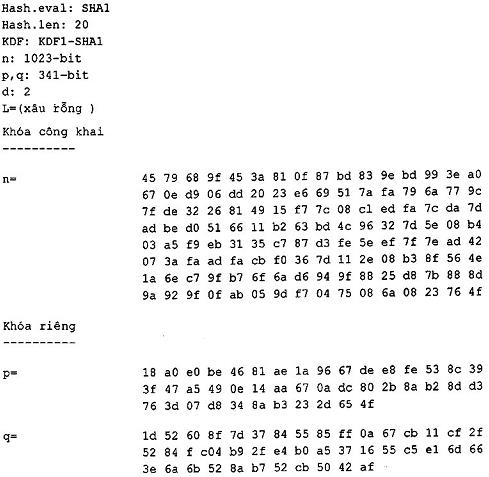

C.8.3. Véc tơ kiểm tra
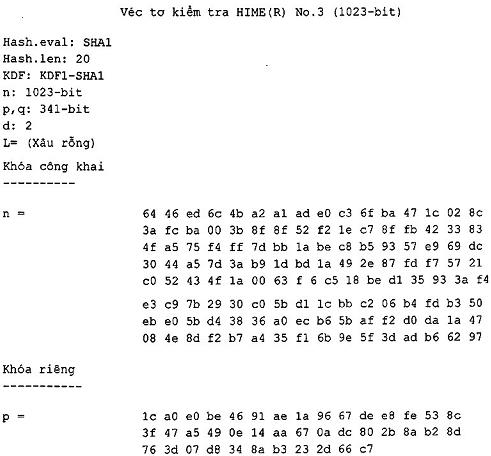

C.8.4. Véc tơ kiểm tra




C.8.5. Véc tơ kiểm tra


C.8.6. Véc tơ kiểm tra



THƯ MỤC TÀI LIỆU THAM KHẢO
[1]. ISO/IEC 10116:1997, Information technology - Security techniques - Modes of operation for an n-bit block cipher
[2]. ISO/I EC 10118 (all parts), Information technology - Security techniques - Hash-functions
[3]. ISO/IEC 11770 (all parts), Information technology - Security techniques - Key management
[4]. ISO/IEC 15946-1:2002, Information technology - Security techniques - Cryptographic techniques based on elliptic curves - Part I: General
[5]. ISO/IEC 18031:2005, Information technology - Security techniques - Random bit generation
[6]. ISO/IEC 18032:2005, Information technology - Security techniques - Prime number generation
[7]. ISO/IEC18033-1:2005, Information technology - Security techniques - Encryption algorithms - Part I: General
[8]. [8] M. Abdalla, M. Bellare, and P. Rogaway. DHAES: an encryption scheme based on the Diffie- Hellman problem. Cryptology ePrint Archive, Report 1999/007, 1999. <http://eprint.iacr.org>
[9]. M. Abdalla, M. Bellare, and P. Rogaway. The Oracle Diffie-Hellman assumptions and an analysis of DHIES. In Topics in Cryptology - CT-RSA 2001, pages 143-158, 2001. Springer LNCS 2045
[10]. M. Bellare, A. Boldyreva, and S. Micali. Public-key encryption in a multi-user setting: security proofs and improvements. In Advances in Cryptology - Eurocrypt 2000, pages 259-274, 2000
[11]. M. Bellare, A. Desai, E. Jokipii, and P. Rogaway. A concrete security treatment of symmetric encryption: analysis of the DES modes of operation. In 38th Annual Symposium on Foundations of Computer Science, 1997
[12]. M. Bellare, A. Desai, D. Pointcheval, and P. Rogaway. Relations among notions of security for public-key encryption schemes. In Advances in Cryptology-Crypto '98, pages 26-45, 1998
[13]. M. Bellare, J. Kilian, and P. Rogaway. On the security of cipher block chaining. In Advances in Cryptology - Crypto '94, pages 341-358, 1994
[14]. M. Bellare and P. Rogaway. Random oracles are practical: a paradigm for designing efficient protocols. In First ACM Conference on Computer and Communications Security, pages 62-73, 1993
[15]. M. Bellare and P. Rogaway. Optimal asymmetric encryption. In Advances in Cryptology - Eurocrypt '94, pages 92-111,1994
[16]. I. Blake, G. Seroussi, and N. Smart. Elliptic Curves in Cryptography. Cambridge University Press, 1999
[17]. D. Boneh. The Decision Diffie-Hellman Problem. In Ants-lll, pages 48-63, 1998. Springer LNCS 1423
[18]. R. Canetti, Universally composable security: a new paradigm for cryptographic protocols. Cryptology ePrint Archive, Report 2000/067, 2000. <http://eprint.iacr.org>
[19]. R. Canetti, O. Goldreich, and S. Halevi. The random oracle methodology, revisited. In 30th Annual ACM Symposium on Theory of Computing, pages 209-218, 1998
[20]. R. Cramer and V. Shoup. A practical public key cryptosystem provably secure against adaptive chosen ciphertext attack. In Advances in Cryptology-Crypto '98, pages 13-25, 1998
[21]. R. Cramer and V. Shoup. Design and analysis of practical public-key encryption schemes secure against adaptive chosen ciphertext attack. Cryptology ePrint Archive, Report 2001/108, 2001. <http://eprint.iacr.org>
[22]. D. Dolev, C. Dwork, and M. Naor. Non-malleable cryptography. In 23rd Annual ACM Symposium on Theory of Computing, pages 542-552,1991
[23]. Dolev, C. Dwork, and M. Naor. Non-malleable cryptography, 1998. Manuscript (updated, full length version of STOC paper)
[24]. Dolev, C. Dwork, and M. Naor. Non-malleable cryptography. SIAM J. Comput., 30(2):391-437, 2000
[25]. T. EIGamal. A public key cryptosystem and signature scheme based on discrete logarithms. IEEE Trans. Inform. Theory, 31:469-472,1985
[26]. Fujisaki and T.Okamoto. Secure integration of asymmetric and symmetric encryption schemes. In Advances in Cryptology-Crypto '99, pages 537-554, 1999
[27]. E. Fujisaki, T. Okamoto, D. Pointcheval, and J. Stern. RSA-OAEP is secure under the RSA assumption. In Advances in Cryptology-Crypto 2001, pages 260-274, 2001
[28]. S. Goldwasser and S. Micali. Probabilistic encryption. Journal of Computer and System Sciences, 28:270-299,1984
[29]. Self-evaluation report: HIME(R) cryptosystem, Oct. 2003. Available from <http://www.sdl.hitachi.co.jp/crypto/hime/index.html>
[30]. H. W. Lenstra. Finding isomorphisms between finite fields. Math. Comp., 56:329-347,1991
[31]. J. Manger. A chosen ciphertext attack on RSA Optimal Asymmetric Encryption Padding (OAEP) as standardized in PKCS # 1 v2.0. In Advances in Cryptology-Crypto 2001, pages 230-238, 2001
[32]. U. Maurer and S. Wolf. The Diffie-Hellman protocol. Designs, Codes, and Cryptography, 19:147-171, 2000
[33]. M. Naor and O. Reingold. Number-theoretic constructions of efficient pseudo-random functions. In 38th Annual Symposium on Foundations of Computer Science, 1997
[34]. M. Naor and M. Yung. Public-key cryptosystems provably secure against chosen ciphertext attacks. In 22nd Annual ACM Symposium on Theory of Computing, pages 427-437,1990
[35]. M. Nishioka, H. Satoh, and K. Sakuri. Design and analysis of fast provably secure public-key cryptosystems based on a modular squaring. In Proc. ICISC 2001, LNCS 2288, pages 81-102, 2001
[36]. T. Okamoto and D. Pointcheval. The gap-problems; a new class of problems for the security of cryptographic schemes. In Proc. 2001 International Workshop on Practice and Theory in Public Key Cryptography (PK.C 2001), 2001
[37]. C. Rackoff and D. Simon. Noninteractive zero-knowledge proof of knowledge and chosen ciphertext attack. In Advances in Cryptology-Crypto '91, pages 433-444,1991
[38]. R. L. Rivest, A. Shamir, and L. M. Adleman. A method for obtaining digital signatures and public-key cryptosystems. Communications of the ACM, 21(2): 120-126, 1978
[39]. V. Shoup. Lower bounds for discrete logarithms and related problems. In Advances in Cryptology - Eurocrypt '97, pages 256-266, 1997
[40]. V. Shoup. OAEP reconsidered. In Advances in Cryptology-Crypto 2001, pages 239-259, 2001
[41]. V. Shoup. A proposal for an ISO Standard for public key encryption. Cryptology ePrint Archive, Report 2001/112, 2001 <http://eprint.iacr.org>
[42]. S. Vaudenay. Security flaws induced by CBC padding - applications to SSL, IPSEC, WTLS. In Advances in Cryptology-Eurocrypt 2002, 2002
MỤC LỤC
Lời nói đầu
Giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Định nghĩa
4. Ký hiệu và khái niệm
5. Cơ sở toán học
6. Các biến đổi mật mã
7. Mật mã phi đối xứng
8. Mật mã lai ghép tổng quát
9. Thiết kết các cơ chế bọc dữ liệu
10. Cơ chế bọc khóa dựa vào EIGamal
11. Mật mã phi đối xứng dựa trên RSA và các cơ chế bọc khóa
12. Mật mã dựa trên phép bình phương modulo
Phụ lục A (Quy định) Cú pháp ASN.1 cho các bộ định danh đối tượng
Phụ lục B (Tham khảo) Xem xét tính an toàn
Phụ lục C (Tham khảo) Các véc tơ kiểm tra
Thư mục tài liệu tham khảo
Bạn chưa Đăng nhập thành viên.
Đây là tiện ích dành cho tài khoản thành viên. Vui lòng Đăng nhập để xem chi tiết. Nếu chưa có tài khoản, vui lòng Đăng ký tại đây!
 Tiêu chuẩn Việt Nam TCVN 11367-2:2016 PDF (Bản có dấu đỏ)
Tiêu chuẩn Việt Nam TCVN 11367-2:2016 PDF (Bản có dấu đỏ) Tiêu chuẩn Việt Nam TCVN 11367-2:2016 DOC (Bản Word)
Tiêu chuẩn Việt Nam TCVN 11367-2:2016 DOC (Bản Word)