- Tổng quan
- Nội dung
- Tiêu chuẩn liên quan
- Lược đồ
- Tải về
Tiêu chuẩn Quốc gia TCVN 10860:2015 ISO 2602:1980 Giải thích thống kê kết quả thử-Ước lượng trung bình-Khoảng tin cậy
| Số hiệu: | TCVN 10860:2015 | Loại văn bản: | Tiêu chuẩn Việt Nam |
| Cơ quan ban hành: | Bộ Khoa học và Công nghệ | Lĩnh vực: | Khoa học-Công nghệ |
|
Ngày ban hành:
Ngày ban hành là ngày, tháng, năm văn bản được thông qua hoặc ký ban hành.
|
2015 |
Hiệu lực:
|
Đã biết
|
| Người ký: | Đang cập nhật |
Tình trạng hiệu lực:
Cho biết trạng thái hiệu lực của văn bản đang tra cứu: Chưa áp dụng, Còn hiệu lực, Hết hiệu lực, Hết hiệu lực 1 phần; Đã sửa đổi, Đính chính hay Không còn phù hợp,...
|
Đã biết
|
TÓM TẮT TIÊU CHUẨN VIỆT NAM TCVN 10860:2015
Nội dung tóm tắt đang được cập nhật, Quý khách vui lòng quay lại sau!
Tải tiêu chuẩn Việt Nam TCVN 10860:2015
TIÊU CHUẨN QUỐC GIA
TCVN 10860:2015
ISO 2602:1980
GIẢI THÍCH THỐNG KÊ KẾT QUẢ THỬ - ƯỚC LƯỢNG TRUNG BÌNH - KHOẢNG TIN CẬY
Statistical interpretation of test results - Estimation of the mean - Confidence interval
Lời nói đầu
TCVN 10860:2015 hoàn toàn tương đương với ISO 2602:1980;
TCVN 10860:2015 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường Chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Lời giới thiệu
Phạm vi của tiêu chuẩn này được giới hạn ở vấn đề riêng biệt. Nó chỉ liên quan đến việc ước lượng trung bình của tổng thể chuẩn trên cơ sở một loạt các thử nghiệm áp dụng với mẫu ngẫu nhiên cá thể lấy từ tổng thể này, đồng thời tiêu chuẩn chỉ đề cập đến trường hợp chưa biết phương sai của tổng thể. Tiêu chuẩn này không đề cập đến việc tính toán khoảng bao gồm ít nhất một tỷ lệ cho trước của tổng thể (giới hạn dung sai thống kê), với xác suất cố định.
Trong ISO 2854 đề cập đến các vấn đề sau đây (bao gồm cả vấn đề được đề cập trong tiêu chuẩn này):
- ước lượng trung bình và hiệu hai trung bình (đã biết hoặc chưa biết phương sai);
- so sánh trung bình với một giá trị đã cho và so sánh hai trung bình với nhau (phương sai đã biết hoặc chưa biết nhưng bằng nhau);
- ước lượng phương sai và tỷ số của hai phương sai;
- so sánh phương sai với giá trị đã cho và so sánh hai phương sai với nhau.
Phương pháp kiểm nghiệm thường được đưa ra cho nhiều phép xác định được tiến hành:
- trên cùng một cá thể (khi thử không phá hủy);
- với các tỷ lệ khác biệt của một sản phẩm có độ đồng nhất cao (ví dụ: chất lỏng);
- trên các cá thể riêng biệt được lấy mẫu từ một tổng thể với lượng biến động nhất định.
Trong hai trường hợp đầu, sai lệch giữa các kết quả thu được chỉ phụ thuộc vào độ lặp lại của phương pháp. Trong trường hợp thứ ba, sai lệch còn phụ thuộc vào độ biến động của bản thân sản phẩm.
Xử lý thống kê các kết quả cho phép tính toán khoảng chứa trung bình của tổng thể các kết quả thu được từ rất nhiều phép xác định, tiến hành trong cùng điều kiện, với một xác suất nhất định. Trong trường hợp cá thể có độ biến động, tiêu chuẩn này giả định rằng các cá thể được tiến hành xác định cấu thành một mẫu ngẫu nhiên từ tổng thể ban đầu và có thể được coi là độc lập.
Khoảng được tính toán như vậy gọi là khoảng tin cậy cho trung bình. Kèm theo nó là mức tin cậy (đôi khi gọi là hệ số tin cậy), là xác suất, thường được biểu thị bằng phần trăm, mà khoảng này chứa trung bình của tổng thể. Trong tiêu chuẩn này chỉ đưa ra các mức 95% và 99%.
GIẢI THÍCH THỐNG KÊ KẾT QUẢ THỬ - ƯỚC LƯỢNG TRUNG BÌNH - KHOẢNG TIN CẬY
Statistical interpretation of test results - Estimation of the mean - Confidence interval
1. Phạm vi áp dụng
Tiêu chuẩn này quy định việc xử lý thống kê các kết quả thử nghiệm cần thiết để tính khoảng tin cậy cho trung bình của tổng thể.
Kết quả thử được biểu thị bằng các phép đo một đặc trưng liên tục. Tiêu chuẩn này không đề cập đến thử nghiệm đặc trưng định tính (ví dụ: có hay không có một tính chất, số khuyết tật, ...)
Phân bố xác suất được lấy làm mô hình toán học cho toàn bộ tổng thể là phân bố chuẩn, đối với phân bố này các thông số, trung bình m và độ lệch chuẩn s là chưa biết.
Giả định về tính chuẩn được thỏa mãn rất rộng: phân bố của các kết quả thu được trong điều kiện thử nghiệm thường là phân bố chuẩn hoặc gần với phân bố chuẩn.
Tuy nhiên, có thể hữu ích khi kiểm tra hiệu lực của giả định về tính chuẩn bằng phương pháp thích hợp.
Việc tính toán có thể được đơn giản hóa bằng cách thay đổi kết quả gốc hoặc đơn vị của kết quả thử nhưng sẽ có rủi ro nếu làm tròn các kết quả này.
Không được loại bỏ bất kỳ quan trắc nào hoặc thực hiện hiệu chính cho các quan trắc đáng ngờ mà không nêu rõ lý giải trên nền tảng thực nghiệm, kỹ thuật hoặc bằng chứng khác.
Phương pháp thử có thể có sai số hệ thống, việc xác định sai số này không được đề cập ở đây. Tuy nhiên, cần chú ý là sự tồn tại của sai số này có thể làm mất hiệu lực của phương pháp. Đặc biệt, nếu có độ chệch không nghi ngờ thì việc tăng cỡ mẫu n không ảnh hưởng đến độ chệch. Các phương pháp đề cập trong ISO 2854 có thể hữu ích trong những trường hợp nhất định để nhận biết sai số hệ thống.
2. Tài liệu viện dẫn
Các tài liệu viện dẫn sau rất cần thiết cho việc áp dụng tiêu chuẩn này. Đối với các tài liệu viện dẫn ghi năm công bố thì áp dụng phiên bản được nêu. Đối với các tài liệu viện dẫn không ghi năm công bố thì áp dụng phiên bản mới nhất, bao gồm cả các sửa đổi, bổ sung (nếu có).
TCVN 8244 (ISO 3534), Thống kê học - Từ vựng và ký hiệu
ISO 2854, Statistical treatment of data - Problems of estimation and tests of means and variances (Xử lý dữ liệu thống kê - Vấn đề ước lượng và kiểm nghiệm trung bình và phương sai)
3. Thuật ngữ, định nghĩa và ký hiệu
Tiêu chuẩn này sử dụng các thuật ngữ, định nghĩa và ký hiệu nêu trong TCVN 8244 (ISO 3534).
4. Ước lượng trung bình
4.1. Trường hợp kết quả không được nhóm thành các lớp
Sau khi loại bỏ mọi kết quả nghi ngờ, loạt gồm n phép đo xi (trong đó i = 1, 2, 3, …, n), một số trong số này có thể cùng giá trị.
Trung bình m của phân bố chuẩn đang xét được ước lượng bằng trung bình cộng của n kết quả:
![]()
4.2. Trường hợp kết quả được nhóm thành các lớp
Khi số lượng kết quả đủ lớn (ví dụ, trên 50) thì sẽ có lợi khi nhóm chúng thành các lớp có cùng độ rộng. Trong các trường hợp nhất định, kết quả cũng có thể thu được trực tiếp đã nhóm thành các lớp.
Tần số của lớp thứ i, tức là số các kết quả trong lớp i, được ký hiệu là ni.
Số lớp được ký hiệu là k, ta có:
![]()
Điểm giữa của lớp i được ký hiệu Ià yi. Khi đó, trung bình m được ước lượng bằng trung bình có trọng số của tất cả các điểm giữa của các lớp:
![]()
5. Khoảng tin cậy cho trung bình
Khoảng tin cậy cho trung bình tổng thể được tính từ các ước lượng của trung bình và ước lượng độ lệch chuẩn.
Phương pháp khác để tính khoảng tin cậy bằng việc sử dụng độ rộng mẫu được nêu trong Phụ lục A.
5.1. Ước lượng độ lệch chuẩn
5.1.1. Trường hợp kết quả không được nhóm thành các lớp
Ước lượng của độ lệch chuẩn s, tính từ bình phương độ lệch so với trung bình cộng, được cho bằng công thức:
![]()
trong đó
xi là giá trị của phép đo thứ i (j = 1, 2, 3, …, n);
n là tổng số các phép đo;
![]() là trung bình cộng của n phép đo, tính như nêu trong 4.1.
là trung bình cộng của n phép đo, tính như nêu trong 4.1.
Để dễ tính toán, khuyến nghị sử dụng công thức sau:
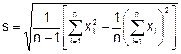
5.1.2. Trường hợp kết quả được nhóm thành các lớp
Trong trường hợp kết quả được nhóm thành các lớp, công thức cho ước lượng độ lệch chuẩn là
![]()
Để dễ tính toán, khuyến nghị sử dụng công thức sau:
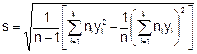
trong đó
yi là điểm giữa của lớp thứ i (i = 1, 2, 3, …, k);
k là tổng số các lớp;
n là tổng số các phép đo;
![]() là trung bình có trọng số của tất cả các điểm giữa của các lớp, tính như nêu trong 4.2.
là trung bình có trọng số của tất cả các điểm giữa của các lớp, tính như nêu trong 4.2.
Trong trường hợp kết quả được nhóm, giá trị tính được s cần được hiệu chính (“hiệu chính Sheppard”). Vì việc hiệu chính này có tầm quan trọng thứ hai nên nó không được đề cập ở đây.
5.2. Khoảng tin cậy cho trung bình
Đối với mức tin cậy được chọn (95 % hoặc 99 %), theo trường hợp cụ thể, phải xác định khoảng tin cậy hai phía hoặc một phía.
5.2.1. Khoảng tin cậy hai phía
Khoảng tin cậy hai phía cho trung bình tổng thể được xác định bằng bất đẳng thức kép sau đây:
a) ở mức tin cậy 95 %:
![]()
b) ở mức tin cậy 99 %:
![]()
5.2.2. Khoảng tin cậy một phía
Khoảng tin cậy một phía cho trung bình tổng thể được xác định bằng một trong hai bất đẳng thức sau đây:
a) ở mức tin cậy 95 %:
![]()
hoặc
![]()
b) ở mức tin cậy 99 %:
![]()
hoặc
![]()
với ![]() , nếu cần, được thay bằng
, nếu cần, được thay bằng ![]() , trong trường hợp kết quả được nhóm thành lớp.
, trong trường hợp kết quả được nhóm thành lớp.
Giá trị t0,975, t0,995, t0,95, t0,99 là các giá trị có phân bố t Student với v = n + 1 bậc tự do.
Các giá trị này được cho trong Bảng 1.
Bảng này cũng đưa ra các giá trị của tỷ số
![]()
Khi giá trị của n lớn hơn 60, ưu tiên để tính giá trị của t bằng nội suy tuyến tính từ ![]() sử dụng Bảng 2.
sử dụng Bảng 2.
Ví DỤ:
n = 250
![]()
t0,995 = 2,576 + 0,48 + (2,617 - 2,576) = 2,596
6. Trình bày kết quả
6.1. Đưa ra biểu thức trung bình theo 4.1 hoặc 4.2.
6.2. Biểu thị khoảng tin cậy dưới dạng bất đẳng thức kép của 5.2.1 hoặc một trong hai bất đẳng thức của 5.2.2, nêu rõ mức tin cậy (95 % hay 99 %). Chỉ ra số kết quả bị loại bỏ do nghi ngờ và lý do loại bỏ.
Bảng 1 - Giá trị của t1-a và tỷ số ![]()
|
| Mức tin cậy | Mức tin cậy |
|
| Mức tin cậy | Mức tin cậy | ||||
| n | 95 % | 99 % | 95 % | 99 % |
| n | 95 % | 99 % | 95 % | 99 % |
| t0,975 | t0,995 | t0,95 | t0,99 |
|
|
|
|
| ||
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 50 60 | 12,71 4,303 3,182 2,776 2,571 2,447 2,365 2,306 2,262 2,228 2,201 2,179 2,160 2,145 2,131 2,120 2,110 2,101 2,093 2,086 2,080 2,074 2,069 2,064 2,060 2,056 2,052 2,048 2,045 2,024 2,008 2,000 | 63,66 9,925 5,841 4,604 4,032 3,707 3,499 3,355 3,250 3,109 3,106 3,055 3,012 2,977 2,947 2,921 2,898 2,878 2,861 2,845 2,831 2,819 2,807 2,707 2,787 2,779 2,771 2,763 2,756 2,707 2,680 2,664 | 6,311 2,920 2,353 2,132 2,015 1,943 1,895 1,860 1,833 1,812 1,796 1,782 1,771 1,761 1,753 1,746 1,740 1,734 1,729 1,725 1,721 1,717 1,714 1,711 1,708 1,706 1,703 1,701 1,699 1,682 1,676 1,673 | 31,82 6,965 4,541 3,747 3,365 3,143 2,998 2,896 2,821 2,704 2,718 2,681 2,650 2,624 2,602 2,583 2,567 2,552 2,639 2,528 2,518 2,508 2,500 2,402 2,485 2,479 2,473 2,467 2,462 2,430 2,404 2,393 |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 50 60 | 8,985 2,484 1,591 1,242 1,049 0,925 0,836 0,769 0,715 0,072 0,635 0,604 0,577 0,554 0,533 0,514 0,497 0,482 0,468 0,455 0,443 0,432 0,422 0,413 0,404 0,396 0,388 0,380 0,373 0,320 0,284 0,258 | 45,013 5,730 2,920 2,059 1,646 1,401 1,237 1,118 1,028 0,900 0,897 0,847 0,805 0,769 0,737 0,708 0,683 0,660 0,640 0,621 0,604 0,588 0,573 0,559 0,547 0,535 0,524 0,513 0,503 0,428 0,379 0,344 | 4,465 1,686 1,177 9,953 0,823 0,734 0,670 0,620 0,580 0,546 0,518 0,494 0,473 0,455 0,438 0,423 0,410 0,398 0,387 0,376 0,367 0,358 0,350 0,342 0,335 0,328 0,322 0,316 0,310 0,266 0,237 0,216 | 22,501 4,021 2,270 1,676 1,374 1,188 1,060 0,966 0,892 0,833 0,785 0,744 0,708 0,668 0,651 0,627 0,605 0,586 0,568 0,552 0,537 0,523 0,510 0,408 0,487 0,477 0,467 0,658 0,449 0,384 0,340 0,309 |
Bảng 2 - Bảng nội suy tuyến tính khi n lớn hơn 60
| n |
| t0,975 | t0,995 | t0,95 | t0,99 |
| 60 | 2 | 2,000 | 2,664 | 1,673 | 2,393 |
| 120 | 1 | 1,980 | 2,617 | 1,658 | 2,358 |
| ¥ | 0 | 1,960 | 2,576 | 1,645 | 2,326 |
Phụ lục A
(quy định)
Khoảng tin cậy cho trung bình theo độ rộng mẫu
Nếu các phép đo được xếp theo thứ tự không giảm về độ lớn, sao cho x1 £ x2 £ … £ xn khi đó w = xn - x1 được gọi là độ rộng mẫu. Vẫn giả định rằng tổng thể có phân bố chuẩn, có thể xác định khoảng tin cậy cho trung bình tổng thể từ độ rộng mẫu khi số phép đo ít, tức là 12 hoặc ít hơn. Thực tế tính toán này có ưu điểm là nhanh hơn; nhược điểm là thường dẫn đến khoảng tin cậy rộng hơn và nhạy hơn với sai lệch so với dạng chuẩn giả định của các quan trắc.
Khoảng tin cậy hai phía
Khoảng tin cậy hai phía cho trung bình tổng thể được xác định bằng bất đẳng thức kép sau đây:
a) ở mức tin cậy 95 %:
![]()
b) ở mức tin cậy 99 %:
![]()
Khoảng tin cậy một phía
Khoảng tin cậy một phía cho trung bình tổng thể được xác định bằng một trong hai bất đẳng thức sau đây:
a) ở mức tin cậy 95 %:
![]()
hoặc
![]()
b) ở mức tin cậy 99 %:
![]()
hoặc
![]()
Các hệ số q0,975, q0,995, q0,95, q0,99,được cho trong Bảng A.1.
Bảng A.1 - Các hệ số q0,975, q0,995, q0,95, q0,99
|
| Mức tin cậy | Mức tin cậy | ||
| 95 % | 99 % | 95 % | 99 % | |
| n | q0,975 | q0,995 | q0,95 | q0,99 |
| 2 | 6,353 | 31,828 | 3,157 | 15,910 |
| 3 | 1,304 | 3,008 | 0,885 | 2,111 |
| 4 | 0,717 | 1,316 | 0,529 | 1,023 |
| 5 | 0,507 | 0,843 | 0,388 | 0,685 |
| 6 | 0,399 | 0,628 | 0,312 | 0,523 |
| 7 | 0,333 | 0,507 | 0,263 | 0,429 |
| 8 | 0,288 | 0,429 | 0,230 | 0,366 |
| 9 | 0,255 | 0,374 | 0,205 | 0,322 |
| 10 | 0,230 | 0,333 | 0,186 | 0,288 |
| 11 | 0,210 | 0,302 | 0,170 | 0,262 |
| 12 | 0,194 | 0,277 | 0,158 | 0,241 |
Nguồn: E. Lord. Sử dụng độ rộng thay cho độ lệch chuẩn trong kiểm nghiệm t (Biometrika, Tập 34, 1947, pp. 41-67), với mục nhập q0,95 (n = 2) được hiệu chỉnh.
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Tài liệu viện dẫn
3. Thuật ngữ, định nghĩa và ký hiệu
4. Ước lượng trung bình
4.1. Trường hợp kết quả không được nhóm thành các lớp
4.2. Trường hợp kết quả được nhóm thành các lớp
5. Khoảng tin cậy cho trung bình
5.1. Ước lượng độ lệch chuẩn
5.2. Khoảng tin cậy cho trung bình
6. Trình bày kết quả
Phụ lục A (quy định) Khoảng tin cậy cho trung bình từ độ rộng mẫu
Bạn chưa Đăng nhập thành viên.
Đây là tiện ích dành cho tài khoản thành viên. Vui lòng Đăng nhập để xem chi tiết. Nếu chưa có tài khoản, vui lòng Đăng ký tại đây!
 Tiêu chuẩn Việt Nam TCVN 10860:2015 PDF (Bản có dấu đỏ)
Tiêu chuẩn Việt Nam TCVN 10860:2015 PDF (Bản có dấu đỏ) Tiêu chuẩn Việt Nam TCVN 10860:2015 DOC (Bản Word)
Tiêu chuẩn Việt Nam TCVN 10860:2015 DOC (Bản Word)