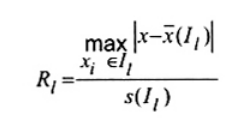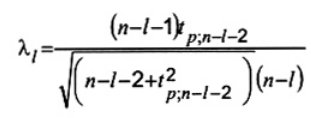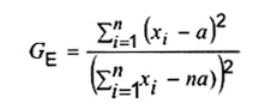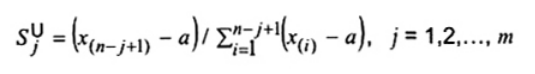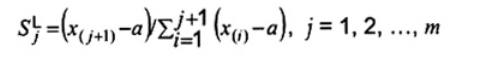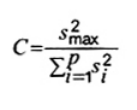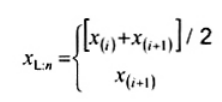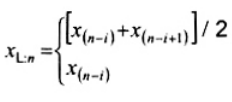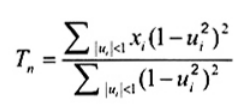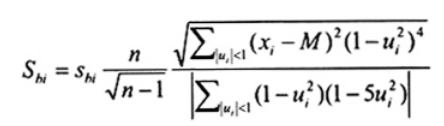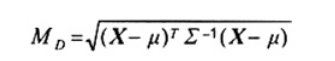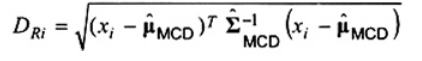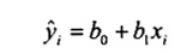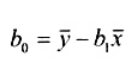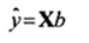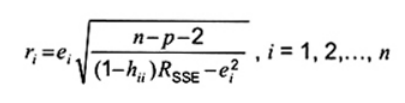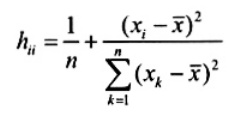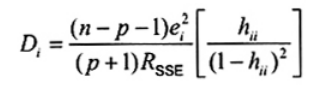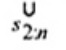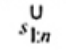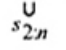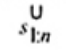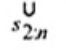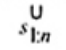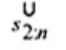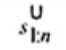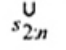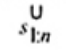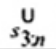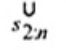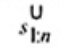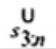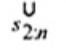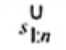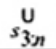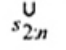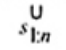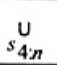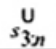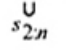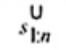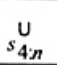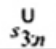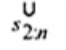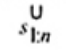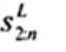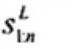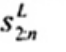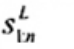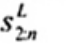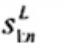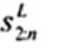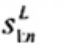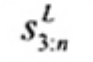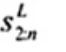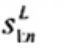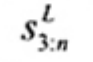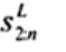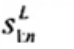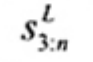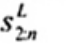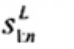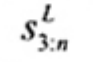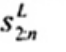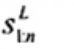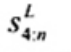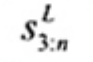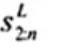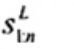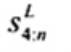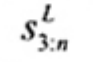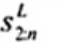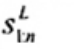- Tổng quan
- Nội dung
- Tiêu chuẩn liên quan
- Lược đồ
- Tải về
Tiêu chuẩn TCVN 8006-4:2013 Kiểm nghiệm thống kê để phát hiện giá trị bất thường trong dữ liệu
| Số hiệu: | TCVN 8006-4:2013 | Loại văn bản: | Tiêu chuẩn Việt Nam |
| Cơ quan ban hành: | Bộ Khoa học và Công nghệ | Lĩnh vực: | Khoa học-Công nghệ |
|
Ngày ban hành:
Ngày ban hành là ngày, tháng, năm văn bản được thông qua hoặc ký ban hành.
|
2013 |
Hiệu lực:
|
Đã biết
|
| Người ký: | Đang cập nhật |
Tình trạng hiệu lực:
Cho biết trạng thái hiệu lực của văn bản đang tra cứu: Chưa áp dụng, Còn hiệu lực, Hết hiệu lực, Hết hiệu lực 1 phần; Đã sửa đổi, Đính chính hay Không còn phù hợp,...
|
Đã biết
|
TÓM TẮT TIÊU CHUẨN VIỆT NAM TCVN 8006-4:2013
Nội dung tóm tắt đang được cập nhật, Quý khách vui lòng quay lại sau!
Tải tiêu chuẩn Việt Nam TCVN 8006-4:2013
TIÊU CHUẨN QUỐC GIA
TCVN 8006-4 : 2013
ISO 16269-4:2010
GIẢI THÍCH CÁC DỮ LIỆU THỐNG KÊ - PHẦN 4: PHÁT HIỆN VÀ XỬ LÝ CÁC GIÁ TRỊ BẤT THƯỜNG
Statistical interpretation of data - Part 4: Detection and treatment of outliers
Lời nói đầu
TCVN 8006-4:2013 hoàn toàn tương đương với ISO 16269-4:2010;
TCVN 8006-4:2013 do Ban kỹ thuật tiêu chuẩn quốc gia TCVN/TC 69 Ứng dụng các phương pháp thống kê biên soạn, Tổng cục Tiêu chuẩn Đo lường chất lượng đề nghị, Bộ Khoa học và Công nghệ công bố.
Bộ tiêu chuẩn TCVN 8006, chấp nhận bộ tiêu chuẩn ISO 16269, gồm các tiêu chuẩn dưới đây có tên chung “Giải thích các dữ liệu thống kê”:
- TCVN 8006-4:2013 (ISO 16269-4:2010), Phần 4: Phát hiện và xử lý các giá trị bất thường
- TCVN 8006-6:2009 (ISO 16269-6:2005), Phần 6: Xác định khoảng dung sai thống kê
- TCVN 8006-7:2013 (ISO 16269-6:2001), Phần 7: Trung vị - Ước lượng và khoảng tin cậy
Bộ tiêu chuẩn ISO 16269 còn có tiêu chuẩn sau:
- ISO 16269-8, Statistical interpretation of data - Part 8: Determination of prediction intervals
Lời giới thiệu
Xác định các giá trị bất thường một trong những vấn đề lâu đời nhất trong giải thích dữ liệu. Nguyên nhân của giá trị bất thường bao gồm sai số đo, sai số lấy mẫu, báo cáo thấp đi hoặc báo cáo cao lên có chủ ý các kết quả lấy mẫu, ghi chép sai, giả định phân bố hay mô hình sai cho tập dữ liệu, các quan trắc hiếm, v.v..
Giá trị bất thường có thể bóp méo và giảm thông tin trong nguồn dữ liệu hoặc cơ chế tạo dữ liệu. Trong công nghiệp chế tạo, sự có mặt các giá trị bất thường sẽ làm giảm hiệu lực của thiết kế quá trình/sản phẩm và quy trình kiểm soát chất lượng. Các giá trị bất thường có thể không nhất thiết là xấu hay sai lầm. Trong một số trường hợp, giá trị bất thường có thể mang thông tin thiết yếu và do đó cần được nhận biết để nghiên cứu thêm.
Nghiên cứu và phát hiện giá trị bất thường từ các quá trình đo mang lại hiểu biết tốt hơn về quá trình và phân tích dữ liệu đúng sẽ dẫn đến những kết luận được cải thiện.
Với một lượng lớn tài liệu đề cập đến chủ đề giá trị bất thường, điều đặc biệt quan trọng đối với cộng đồng quốc tế là xác định và chuẩn hóa tập các phương pháp sử dụng trong việc nhận biết và xử lý các giá trị bất thường. Việc áp dụng tiêu chuẩn này cho phép doanh nghiệp và ngành công nghiệp thừa nhận các phân tích dữ liệu do các quốc gia hay tổ chức thành viên tiến hành.
Tiêu chuẩn gồm sáu phụ lục. Phụ lục A đưa ra thuật toán để tính thống kê kiểm nghiệm và các giá trị tới hạn của quy trình phát hiện giá trị bất thường trong tập dữ liệu lấy từ phân bố chuẩn. Phụ lục B, D và E cung cấp các bảng cần thiết để thực hiện các quy trình khuyến nghị. Phụ lục C cung cấp các bảng và lý thuyết thống kê làm cơ sở cho việc vẽ các đồ thị hộp sửa đổi trong phát hiện giá trị bất thường. Phụ lục F đưa ra hướng dẫn có cấu trúc và lưu đồ các quá trình khuyến nghị trong tiêu chuẩn này.
GIẢI THÍCH CÁC DỮ LIỆU THỐNG KÊ - PHẦN 4: PHÁT HIỆN VÀ XỬ LÝ CÁC GIÁ TRỊ BẤT THƯỜNG
Statistical interpretation of data - Part 4: Detection and treatment of outliers
1. Phạm vi áp dụng
Tiêu chuẩn này đưa ra mô tả chi tiết về quy trình kiểm nghiệm thống kê vững chắc và các phương pháp phân tích dữ liệu bằng đồ thị dùng cho việc phát hiện các giá trị bất thường trong dữ liệu thu được từ các quá trình đo. Tiêu chuẩn khuyến nghị ước lượng ổn định vững chắc và quy trình kiểm nghiệm để thỏa hiệp với sự có mặt của các giá trị bất thường.
Tiêu chuẩn này được xây dựng chủ yếu cho việc phát hiện và sự thích ứng của các giá trị bất thường từ dữ liệu đơn biến. Hướng dẫn nhất định cũng được cung cấp đối với dữ liệu đa biến và hồi quy.
2. Thuật ngữ và định nghĩa
Tiêu chuẩn này áp dụng các thuật ngữ, định nghĩa dưới đây
2.1. Mẫu (sample)
Tập dữ liệu (data set)
Phân tập tổng thể gồm một hoặc nhiều đơn vị mẫu.
CHÚ THÍCH 1: Đơn vị mẫu có thể là cá thể, các trị số hoặc thậm chí là các thực thể trừu tượng phụ thuộc vào tổng thể quan tâm.
CHÚ THÍCH 2: Mẫu từ một tổng thể phân bố chuẩn (2.22), gamma (2.23), hàm mũ (2.24), Weibull (2.25), loga chuẩn (2.26) hay cực trị loại I (2.27) thường được đề cập tương ứng là mẫu chuẩn, gamma, hàm mũ, Weibull, loga chuẩn hay cực trị loại I.
2.2. Giá trị bất thường (outlier)
Thành phần của phân tập nhỏ các quan trắc dường như là không khớp với phần còn lại của mẫu (2.1) đã cho.
CHÚ THÍCH 1: Việc phân loại quan trắc hoặc phân tập các quan trắc là giá trị bất thường chỉ có quan hệ với mô hình được chọn cho tổng thể từ đó tập dữ liệu hình thành. Những quan trắc này không được coi là các thành phần thực sự của tổng thể chính.
CHÚ THÍCH 2: Giá trị bất thường có thể bắt nguồn từ tổng thể cơ sở khác hoặc là kết quả của sự ghi chép không chính xác hoặc sai số đo thô.
CHÚ THÍCH 3: Phân tập có thể gồm một hoặc nhiều quan trắc.
2.3. Che khuất (masking)
Sự xuất hiện của nhiều hơn một giá trị bất thường (2.2) gây khó khăn cho việc phát hiện từng giá trị bất thường.
2.4. Tỷ lệ ngoại vi (some-outside rate)
Xác suất để một hoặc nhiều quan trắc trong mẫu không pha tạp bị phân loại nhầm là giá trị bất thường (2.2).
2.5. Phương pháp thỏa hiệp giá trị bất thường (outlier accommodation method)
Phương pháp không nhạy đối với sự có mặt của các giá trị bất thường (2.2) khi đưa ra kết luận về tổng thể.
2.6. Ước lượng bền (resistant estimation)
Phương pháp ước lượng đưa ra các kết quả chỉ thay đổi đôi chút khi thay thế một phần nhỏ các giá trị dữ liệu trong tập dữ liệu (2.1), có thể với giá trị dữ liệu rất khác biệt với dữ liệu ban đầu.
2.7. Ước lượng ổn định (robust estimation)
Phương pháp ước lượng không nhạy với sai lệch nhỏ so với giả định về mô hình xác suất cơ sở của dữ liệu.
CHÚ THÍCH: Ví dụ là phương pháp ước lượng áp dụng tốt cho phân bố chuẩn (2.22) và vẫn khá tốt nếu phân bố thực tế đối xứng lệch hoặc nặng đuôi. Các loại phương pháp như vậy bao gồm ước lượng L [trung bình có trọng số của thống kê thứ tự (2.10)] và phương pháp ước lượng M (xem Tài liệu tham khảo [9])
2.8. Thứ hạng (rank)
Vị trí của giá trị quan trắc trong một tập hợp các giá trị quan trắc sắp xếp theo thứ tự.
CHÚ THÍCH 1: Các giá trị quan trắc được sắp xếp theo thứ tự tăng (đếm từ dưới lên) hoặc thứ tự giảm (đếm từ trên xuống).
CHÚ THÍCH 2: Với mục đích của tiêu chuẩn này, các giá trị quan trắc giống nhau được phân thứ hạng như chúng khác nhau đôi chút.
2.9. Độ sâu (depth)
<đồ thị hộp> giá trị nhỏ hơn trong hai thứ hạng (2.8) được xác định bằng cách tính từ giá trị nhỏ nhất của mẫu (2.1) trở lên hoặc tính từ giá trị lớn nhất trở xuống.
CHÚ THÍCH 1: Độ sâu có thể không phải là giá trị nguyên (xem Phụ lục C).
CHÚ THÍCH 2: Đối với tất cả các giá trị tóm lược không phải là trung vị (2.11), một độ sâu cho xác định hai giá trị (dữ liệu), một giá trị dưới trung vị và giá trị kia trên trung vị. Ví dụ, hai giá trị dữ liệu với độ sâu 1 là giá trị nhỏ nhất (tối thiểu) và giá trị lớn nhất (tối đa) trong mẫu (2.1) đã cho.
2.10. Thống kê thứ tự (order statistic)
Thống kê xác định bởi thứ tự của nó trong một sắp xếp không giảm của các biến ngẫu nhiên.
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 1.9]
CHÚ THÍCH 1: Cho giá trị quan trắc của một mẫu ngẫu nhiên {x1, x2,…, xn}. Sắp xếp lại các giá trị quan trắc theo thứ tự không giảm được ấn định là x(1) ≤ x(2) ≤ … ≤ x(k) ≤ … ≤ x(n); khi đó x(k) là giá trị quan trắc của thống kê thứ tự thứ k trong mẫu cỡ n.
CHÚ THÍCH 2: Trong thực tế, lập được các thống kê thứ tự cho lượng mẫu (2.1) là việc sắp xếp dữ liệu như được mô tả trong chú thích 1.
2.11. Trung vị (median)
Trung vị mẫu (sample median)
Trung vị của một tập hợp số (median of a set of numbers)
Q2
Thống kê thứ tự (2.10) thứ [(n + 1)/2], nếu cỡ mẫu n là lẻ; tổng của thống kê thứ tự thứ [n/2] và thứ [(n/2) + 1] chia cho 2, nếu cỡ mẫu n là chẵn.
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 1.13]
CHÚ THÍCH: Trung vị mẫu là tứ phân vị thứ hai (Q2)
2.12. Tứ phân vị thứ nhất (first quartile)
Tứ phân vị mẫu dưới (sample lower quartile)
Q1
Đối với số lượng quan trắc lẻ, là trung vị (2.11) của (n - 1)/2 giá trị quan trắc nhỏ nhất, đối với số lượng quan trắc chẵn, là trung vị của n/2 giá trị quan trắc nhỏ nhất.
CHÚ THÍCH 1: Có nhiều định nghĩa khác nhau trong tài liệu về từ phân vị mẫu, đưa ra các kết quả hơi khác nhau. Định nghĩa này được chọn vì dễ ứng dụng cũng như vì nó được sử dụng rộng rãi.
CHÚ THÍCH 2: Các khái niệm như là điểm bản lề hoặc phần tư (2.19 và 2.20) là các biến phổ biến của tứ phân vị. Trong một số trường hợp (xem Chú thích 3 cho 2.19), tứ phân vị thứ nhất và phần tư dưới (2.19) giống hệt nhau.
2.13. Tứ phân vị thứ ba (third quartile)
Tứ phân vị mẫu trên (sample upper quartile)
Q3
Đối với số lượng quan trắc lẻ, là trung vị của (n - 1)/2 giá trị quan trắc lớn nhất; đối với số lượng quan trắc chẵn, là trung vị của n/2 giá trị quan trắc lớn nhất.
CHÚ THÍCH 1: Có nhiều định nghĩa khác nhau trong tài liệu về tứ phân vị mẫu, đưa ra các kết quả hơi khác nhau. Định nghĩa này được chọn vì dễ ứng dụng cũng như vì nó được sử dụng rộng rãi.
CHÚ THÍCH 2: Các khái niệm như là điểm bản lề hoặc phần tư (2.19 và 2.20) là các biến thể phổ biến của tứ phân vị. Trong một số trường hợp (xem chú thích 3 cho 2.20), tứ phân vị thứ ba và phần tư trên (2.20) giống hệt nhau.
2.14. Khoảng tứ phân vị (interquartile range)
IQR
Hiệu giữa tứ phân vị thứ ba (2.13) và tứ phân vị thứ nhất (2.12)
CHÚ THÍCH 1: Đây là một trong những thống kê được sử dụng rộng rãi để mô tả khoảng của tập dữ liệu.
CHÚ THÍCH 2: Hiệu giữa phần tư trên (2.20) và phần tư dưới (2.19) được gọi là khoảng thứ tư và đôi khi được sử dụng thay cho khoảng tứ phân vị.
2.15. Năm số tóm lược (five-number summary)
Số nhỏ nhất, tứ phân vị thứ nhất (2.12), trung vị (2.11), tứ phân vị thứ ba (2.13) và số lớn nhất.
CHÚ THÍCH: Năm số tóm lược cung cấp thông tin bằng số về vị trí, độ trải và độ rộng.
2.16. Đồ thị hộp (box plot)
Trình bày bằng đồ thị nằm ngang hoặc thẳng đứng của năm số tóm lược (2.15).
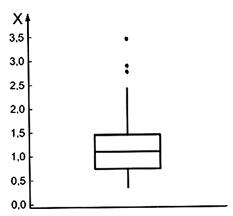
CHÚ THÍCH 1: Đối với đồ thị nằm ngang, tứ phân vị thứ nhất (2.12) và tứ phân vị thứ ba (2.13) được vẽ tương ứng là bên trái và bên phải của hộp, trung vị (2.11) được vẽ là một vạch đứng trong hộp, các nét kéo dài từ tứ phân vị thứ nhất xuống đến giá trị nhỏ nhất hoặc trên rào chắn dưới (2.17) và từ tứ phân vị thứ ba lên đến giá trị lớn nhất tại hoặc dưới rào chắn trên (2.18), và (các) giá trị quá rào chắn trên và rào chắn dưới được đánh dấu riêng là giá trị bất thường (2.2). Đối với đồ thị thẳng đứng, tứ phân vị thứ nhất và tứ phân vị thứ ba được vẽ tương ứng là phần đáy và phần đỉnh của hộp, trung vị được vẽ là một vạch ngang trong hộp, nét kéo dài từ tứ phân vị thứ nhất xuống đến giá trị nhỏ nhất tại hoặc trên rào chắn dưới và từ tứ phân vị thứ ba lên đến giá trị lớn nhất tại hoặc dưới rào chắn trên và (các) giá trị vượt quá rào chắn trên và rào chắn dưới được đánh dấu là (các) giá trị bất thường.
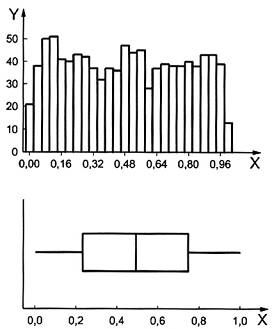
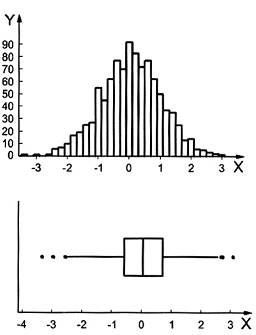
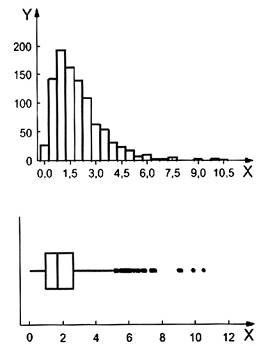
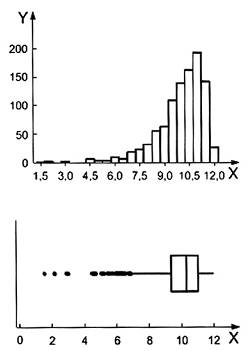
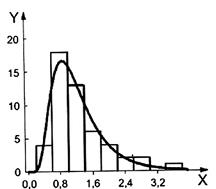
CHÚ THÍCH 2: Chiều rộng hộp và chiều dài rìa của đồ thị hộp cung cấp thông tin bằng đồ thị về vị trí, độ trải, độ bất đối xứng, độ dài đuôi và các giá trị bất thường của mẫu. So sánh giữa các đồ thị hộp và hàm mật độ của phân bố a) đều, b) hình chuông, c) bất đối xứng phải và d) bất đối xứng trái được đưa ra trong các đồ thị ở Hình 1. Trong mỗi phân bố, có một biểu đồ tần số được trình bày phía trên đồ thị hộp.
CHÚ THÍCH 3: Đồ thị hộp được xây dựng với rào chắn dưới (2.17) và rào chắn trên (2.18) được đánh giá bằng cách lấy k là giá trị dựa trên cỡ mẫu n và kiến thức về sự phân bố phổ biến của dữ liệu mẫu được gọi là đồ thị hộp sửa đổi (xem ví dụ, Hình 2). Cấu trúc của một đồ thị hộp sửa đổi được nêu trong 4.4.
|
|
|
| a) Phân bố đều | b) phân bố hình vuông |
|
|
|
| c) Phân bố bất đối xứng bên phải | d) Phân bố bất đối xứng bên trái |
CHÚ DẪN:
X giá trị dữ liệu Y tần số
Trong mỗi phân bố, biểu đồ tần số được trình bày phía trên đồ thị hộp.
Hình 1 - Đồ thị hộp và biểu đồ cột đối với phân bố a) đều, b) hình chuông, c) phân bố đối xứng bên phải và d) đối xứng bên trái
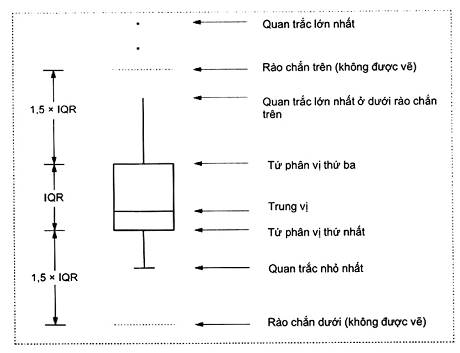
Hình 2 - Đồ thị hộp được chỉnh sửa với rào chắn dưới và trên
2.17. Rào chắn dưới (lower fence)
Ngưỡng giá trị bất thường dưới (lower outlier cut-off)
Giá trị liền kề dưới (lower adjacent value)
Giá trị trong đồ thị hộp (2.16) nằm cách k lần khoảng tứ phân vị (2.14) ở dưới tứ phân vị thứ nhất (2.12), với giá trị k được xác định trước.
CHÚ THÍCH: Trong phần mềm thống kê có bản quyền, rào chắn dưới thường được lấy là Q1 - k (Q3 - Q1) với k được lấy là 1,5 hoặc 3,0. Trước đây, rào chắn này được gọi là “rào chắn dưới bên trong” khi k là 1,5 và “rào chắn dưới bên ngoài” khi k là 3,0.
2.18. Rào chắn trên (upper fence)
Ngưỡng giá trị bất thường trên (upper outlier cut-off)
Giá trị liền kề trên (upper adjacent value)
Giá trị trong đồ thị hộp nằm cách k lần khoảng tứ phân vị (2.14) ở trên tứ phân vị thứ ba (2.13), với giá trị k được xác định trước.
CHÚ THÍCH: Trong phần mềm thống kê có bản quyền, rào chắn trên thường được lấy là Q3 + k (Q3 - Q1) với k được lấy là 1,5 hoặc 3,0. Trước đây, rào chắn này được gọi là “rào chắn trên bên trong” khi k là 1,5 và “rào chắn trên bên ngoài” khi k là 3,0.
2.19. Phần tư dưới (lower fourth)
xL:n
Đối với tập giá trị quan trắc x(1) ≤ x(2) ≤ … ≤ x(n), là đại lượng 0,5 [x(i) + x(i + 1)] khi f = 0 hoặc x(i + 1) khi f > 0, trong đó i là phần nguyên của n/4 và f là phân phân số của n/4.
CHÚ THÍCH 1: Định nghĩa này về phần tư dưới được sử dụng để xác định giá trị khuyến nghị của kL và kU nêu trong Phụ lục C và là giá trị mặc định hoặc tùy chọn trong một số phần mềm thống kê được sử dụng rộng rãi.
CHÚ THÍCH 2: Phần tư dưới và phần tư trên (2.20) là một cặp đôi khi được gọi là điểm bản lề.
CHÚ THÍCH 3: Phần tư dưới đôi khi được gọi là tứ phân vị thứ nhất (2.12).
CHÚ THÍCH 4: Khi f = 0; 0,5 hoặc 0,75, phần tư dưới giống như tứ phân vị thứ nhất. Ví dụ:
| Cỡ mẫu | i = phần nguyên của n/4 | f = phần phân số của n/4 | Tứ phân vị thứ nhất | Phần tư dưới |
| 9 | 2 | 0,25 | [x(2) + x(3)]/2 | x(3) |
| 10 | 2 | 0,50 | x(3) | x(3) |
| 11 | 2 | 0,75 | x(3) | x(3) |
| 12 | 3 | 0 | [x(3) + x(4)]/2 | [x(3) + x(4)]/2 |
2.20. Phần tư trên (upper fourth)
xU:n
Đốivới tập giá trị quan trắc x(1) ≤ x(2) ≤ … ≤ x(n), là đại lượng 0,5 [x(n - i) + x(n - i + 1)] khi f = 0 hoặc x(n-i) khi f > 0, nếu i là phần nguyên của n/4 và f là phần phân số của n/4.
CHÚ THÍCH 1: Định nghĩa này về phần tư trên được sử dụng để xác định giá trị khuyến nghị của kL và kU nêu trong Phụ lục C và là giá trị mặc định hoặc tùy chọn trong một số phần mềm thống kê được sử dụng rộng rãi.
CHÚ THÍCH 2: Phần tư dưới (2.19) và phần tư trên là một cặp đôi khi được gọi là điểm bản lề.
CHÚ THÍCH 3: Phần tư trên đôi khi được đề cập đến như là tứ phân vị thứ ba (2.13).
CHÚ THÍCH 4: Khi f = 0; 0,5 hoặc 0,75, phần tư trên đúng bằng tứ phân vị thứ ba. Ví dụ:
| Cỡ mẫu | i = phần nguyên của n/4 | f = phần phân số của n/4 | Tứ phân vị thứ nhất | Phần tư dưới |
| 9 | 2 | 0,25 | [x(7) + x(8)]/2 | x(7) |
| 10 | 2 | 0,50 | x(8) | x(8) |
| 11 | 2 | 0,75 | x(8) | x(9) |
| 12 | 3 | 0 | [x(9) + x(10)]/2 | [x(9) + x(10)]/2 |
2.21. Sai lầm loại I (type I error)
Bác bỏ giả thuyết không trong khi trên thực tế giả thuyết không là đúng.
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 1.46]
CHÚ THÍCH 1: Sai lầm loại I là một quyết định sai. Do đó, mong muốn duy trì xác suất đưa ra quyết định sai như vậy càng nhỏ càng tốt.
CHÚ THÍCH 2: Có khả năng trong một số tình huống (ví dụ, phép kiểm nghiệm tham số nhị phân p), mức ý nghĩa quy định trước 0,05 là không thể đạt được do sự rời rạc của các kết quả.
2.22. Phân bố chuẩn (normal distribution)
Phân bố Gaussian (Gaussian distribution)
Phân bố liên tục có hàm mật độ xác suất
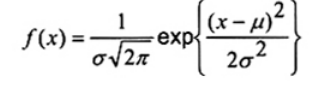
Trong đó -¥ < x < ¥ và với các tham số -¥ < µ < ¥ và s > 0
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.50]
CHÚ THÍCH 1: Tham số vị trí µ là trung bình và tham số thang đo s là độ lệch chuẩn của phân bố chuẩn.
CHÚ THÍCH 2: Mẫu chuẩn là một mẫu (2.1) ngẫu nhiên, được lấy từ một tổng thể tuân theo phân bố chuẩn.
2.23. Phân bố gama (gamma distribution)
Phân bố liên tục có hàm mật độ xác suất
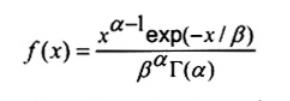
trong đó x > 0 và các tham số a > 0, b > 0
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.56]
CHÚ THÍCH 1: Phân bố gamma được sử dụng trong các ứng dụng liên quan tới độ tin cậy đối với mô hình thời gian tính đến khi hỏng. Phân bố này bao gồm phân bố hàm mũ (2.24) là trường hợp đặc biệt cũng như các trường hợp khác có tỷ lệ hỏng tăng theo tuổi đời.
CHÚ THÍCH 2: Trung bình của phân bố gamma là ab. Phương sai của phân bố gamma là ab2.
CHÚ THÍCH 3: Mẫu gamma là mẫu (2.1) ngẫu nhiên, được lấy từ một tổng thể tuân theo phân bố gamma.
2.24. Phân bố hàm mũ (exponential distribution)
Phân bố liên tục có hàm mật độ xác suất
f(x) = b-1 exp (-x / b)
trong đó x > 0 với tham số b > 0
[TCVN 8244-1:2010 (iso 3534-1:2006), định nghĩa 2.58]
CHÚ THÍCH 1: Phân bố hàm mũ cung cấp cơ sở cho các ứng dụng liên quan đến độ tin cậy, tương ứng với trường hợp “không lão hóa” hoặc tính chất không có nhớ.
CHÚ THÍCH 2: Trung bình của phân bố hàm mũ là b. Phương sai của phân bố hàm mũ là b2.
CHÚ THÍCH 3: Mẫu hàm mũ là mẫu (2.1) ngẫu nhiên, được lấy từ một tổng thể tuân theo phân bố hàm mũ.
2.25. Phân bố Weibull (Weibull distribution)
Phân bố cực trị loại III (type III extreme-value distribution)
Phân bố liên tục có hàm mật độ xác suất
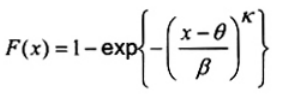
Trong đó x > q với các tham số -¥ < q < ¥, b > 0, k > 0
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.63]
CHÚ THÍCH 1: Ngoài việc dùng như một trong ba phân bố giới hạn có thể có của thống kê thứ tự cực trị, phân bố Weibull chiếm vị trí quan trọng trong các ứng dụng khác nhau, đặc biệt là về độ tin cậy và kỹ thuật. Phân bố Weibull đã chứng tỏ cung cấp sự phù hợp áp dụng cho nhiều loại tập dữ liệu khác nhau.
CHÚ THÍCH 2: Tham số q là tham số vị trí hoặc tham số ngưỡng theo nghĩa là giá trị nhỏ nhất có thể có được trong phân bố Weibull. Tham số b là một tham số thang đo (liên quan đến độ lệch chuẩn của biến Weibull). Tham số k là tham số định dạng.
CHÚ THÍCH 3: Mẫu Weibull là mẫu (2.1) ngẫu nhiên, được lấy từ tổng thể tuân theo phân bố Weibull.
2.26. Phân bố lôga chuẩn (lognormal distribution)
Phân bố liên tục có hàm mật độ xác suất
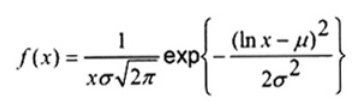
trong đó x > 0 và với các tham số -¥ < µ < ¥ và s > 0
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.52]
2.27. Phân bố cực trị loại I (type I extreme-value distribution)
Phân bố Gumbel (Gumbel distribution)
Phân bố liên tục có hàm mật độ xác suất
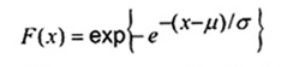
trong đó -¥ < x < ¥ và với các tham số -¥ < µ < ¥ và s > 0
CHÚ THÍCH: Phân bố cực trị đưa ra phân bố tham chiếu thích hợp cho các thống kê thứ tự (2.10) cực trị x(1) và x(n).
[TCVN 8244-1:2010 (ISO 3534-1:2006), định nghĩa 2.61]
3. Ký hiệu
Tiêu chuẩn này sử dụng các ký hiệu và thuật ngữ viết tắt dưới đây:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| - |
|
| - |
|
|
|
|
|
|
|
4. Giá trị bất thường torng dữ liệu đơn biến
4.1. Khái quát
4.1.1. Giá trị bất thường là gì?
Trong trường hợp đơn giản nhất, giá trị bất thường là một quan trắc dường như là không khớp với phần còn lại của tập dữ liệu đã cho. Nhìn chung, có nhiều hơn một giá trị bất thường tại một hoặc cả hai đầu của tập dữ liệu. Vấn đề là xác định xem các quan trắc không phù hợp rõ ràng có phải là giá trị bất thường trong thực tế hay không. Việc xác định này được thực hiện bằng kiểm nghiệm ý nghĩa xác định trước đối với các phân bố phổ biến được giả định. Các quan trắc dẫn đến kết quả có ý nghĩa được coi là giá trị bất thường đối với phân bố đó.
Không thể nhấn mạnh quá tầm quan trọng của việc sử dụng phân bố phổ biến đúng trong kiểm nghiệm giá trị bất thường. Thông thường trong thực tế, phân bố chuẩn cơ bản được giả định khi dữ liệu phát sinh từ một phân bố khác nhau. Giả định sai như vậy có thể dẫn đến phân loại sai quan trắc là các giá trị bất thường.
4.1.2. Nguyên tắc của các giá trị bất thường là gì?
Các quan trắc bất thường hoặc giá trị bất thường điển hình là do một hoặc nhiều nguyên nhân sau đây (xem Tài liệu tham khảo [1] về chi tiết hơn):
a) Sai số đo hoặc ghi chép. Các phép đo được tạo ra không chính xác, quan trắc không đúng, ghi chép sai hoặc nhập sai vào cơ sở dữ liệu.
b) Pha tạp. Dữ liệu phát sinh từ hai hay nhiều phân bố, nghĩa là phân bố phổ biến và một hoặc nhiều phân bố pha tạp. Nếu các phân bố pha tạp có giá trị trung bình khác đáng kể, độ lệch chuẩn lớn hơn và/hoặc đuôi nặng hơn phân bố phổ biến, thì khi đó có xác suất để quan trắc cực trị xuất phát từ phân bố pha tạp có thể xuất hiện như giá trị bất thường trong phân bố phổ biến.
CHÚ THÍCH 1: Nguyên nhân của sự pha tạp có thể là do sai số lấy mẫu trong đó một phần nhỏ của dữ liệu mẫu vô tình được coi là được lấy từ một tổng thể khác với phần còn lại của dữ liệu mẫu; hay báo cáo thiếu hoặc báo cáo quá có chủ ý về thực nghiệm hay điều tra lấy mẫu.
c) Giả định phân bố sai. Tập dữ liệu được coi như rút ra từ một phân bố cụ thể, nhưng lại được xem như là lấy từ một phân bố khác.
VÍ DỤ: Tập dữ liệu được xem như là lấy từ một phân bố chuẩn, nhưng lại được xem như là lấy từ một phân bố bất đối xứng cao (ví dụ, hàm mũ hoặc lôga chuẩn) hoặc phân bố đối xứng nhưng đuôi nặng hơn (ví dụ phân bố t). Do đó, quan trắc bị chệch khỏi vị trí trung tâm có thể bị ghi sai là giá trị bất thường mặc dù chúng là các quan trắc hợp lệ đối với phân bố bất đối xứng cao hoặc phân bố nặng đuôi.
d) Quan trắc hiếm. Quan trắc không có khả năng xuất hiện vẫn có thể xuất hiện trong các trường hợp hiếm, trong các mẫu được coi là lấy từ phân bố xác suất giả định. Các quan trắc cực trị này thường được gán sai là các giá trị bất thường do hiếm khi xảy ra, nhưng chúng không thực sự là giá trị bất thường.
CHÚ THÍCH 2: Sự xuất hiện của quan trắc hiếm khi phân bố phổ biến là đối xứng nhưng nặng đuôi có thể dẫn đến các giả định phân bố sai.
4.1.3. Tại sao cần phát hiện các giá trị bất thường?
Các giá trị bất thường không nhất thiết là xấu hay sai lỗi. Chúng có thể được lấy làm một dấu hiệu về sự tồn tại hiện tượng hiếm có thể là lý do cho việc nghiên cứu thêm. Ví dụ, nếu một giá trị bất thường chỉ gây ra do xử lý công nghiệp cụ thể thì có thể thực hiện những phát kiến quan trọng bằng cách điều tra nguyên nhân.
Nhiều kỹ thuật thống kê và thống kê tóm lược nhạy cảm với sự xuất hiện của các giá trị bất thường. Ví dụ, trung bình mẫu và độ lệch chuẩn mẫu dễ bị ảnh hưởng bởi sự có mặt ngay cả của một giá trị bất thường duy nhất mà có thể dẫn đến những kết luận không hợp lệ.
Việc nghiên cứu tính chất và tần suất của các giá trị bất thường trong một vấn đề cụ thể có thể dẫn đến những sửa đổi thích hợp về phân bố hoặc giả định mô hình liên quan đến tập dữ liệu và cũng dẫn đến việc lựa chọn phù hợp các phương pháp ổn định có thể chấp nhận sự xuất hiện của giá trị bất thường có thể trong các phân tích dữ liệu tiếp theo và do đó dẫn đến những kết luận được cải thiện (xem Điều 6).
4.2. Sàng lọc dữ liệu
Sàng lọc dữ liệu có thể bắt đầu với việc kiểm tra đơn giản bằng mắt tập dữ liệu nhất định. Đồ thị dữ liệu đơn giản, như đồ thị điểm, đồ thị phân tán, biểu đồ, đồ thị thân và lá, đồ thị xác suất, đồ thị hộp, đồ thị theo chuỗi thời gian hoặc sắp xếp dữ liệu theo thứ tự không giảm về độ lớn, có thể cho thấy nguồn biến động ngoài dự đoán và các điểm dữ liệu cực trị/bất thường. Ví dụ phân bố nhị thức của tập dữ liệu được thể hiện bằng biểu đồ hoặc đồ thị thân và lá có thể là bằng chứng của mẫu pha tạp hoặc sự pha trộn dữ liệu được coi là lấy từ hai tổng thể khác nhau. Khuyến nghị dùng đồ thị xác suất và đồ thị hộp cho việc nhận biết các điểm dữ liệu cực trị/bất thường. Khi đó, những giá trị bất thường có thể có này được nghiên cứu thêm bằng cách sử dụng các phương pháp nêu trong 4.3 hoặc 4.4.
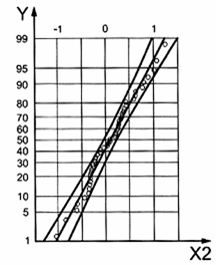
Đồ thị xác suất không chỉ cung cấp kiểm nghiệm bằng đồ thị việc quan trắc hoặc phần lớn các quan trắc có thể được coi là theo phân bố giả định hay không; mà còn cho thấy các quan trắc bất thường trong tập dữ liệu. Các điểm dữ liệu lệch rõ rệt khỏi đường thẳng khớp bằng mắt với các điểm trên đồ thị xác suất có thể được xem có khả năng là các giá trị bất thường. Đồ thị xác suất của nhiều phân bố được cung cấp trong phần mềm có bản quyền.
Đồ thị hộp là một trong những công cụ đồ thị phổ biến nhất cho việc khai thác dữ liệu. Việc hiển thị vị trí trung tâm, độ trải và dạng phân bố của tập dữ liệu rất hữu ích. Rào chắn trên và dưới của đồ thị hộp được xác định là
| rào chắn dưới = Q1 - k (Q3 - Q1) rào chắn trên = Q1 + k (Q3 - Q1) | (1) |
Trong đó Q1 và Q3 là tứ phân vị thứ nhất và thứ ba của tập dữ liệu và k là hằng số.
Tukey[2] gọi giá trị dữ liệu nằm ngoài rào chắn trên và dưới với k = 1,5 là các giá trị bất thường có thể (có thể) nghi ngờ và các giá trị bất thường nằm ngoài rào chắn với k = 3,0 là các giá trị bất thường cực trị.
CHÚ THÍCH 1: Bảng đồ thị xác suất đối với phân bố chuẩn, phân bố hàm mũ, phân bố lôga chuẩn có thể vẫn được sử dụng tại thời điểm công bố từ http://www.weibull.com/GPaper/index.htm.
CHÚ THÍCH 2: Loại đồ thị xác suất nên phụ thuộc vào giả định phân bố của tổng thể. Ví dụ, cần sử dụng đồ thị xác suất hàm mũ nếu được giả định hoặc có kiến thức ưu tiên, là tập dữ liệu có thể được xem là lấy từ tổng thể dạng hàm mũ.
CHÚ THÍCH 3: Một số lượng lớn các quan trắc có thể được nhận biết sai là các giá trị bất thường tiềm ẩn bằng đồ thị hộp với rào chắn trên và dưới xác định theo phương trình (1) khi tập dữ liệu có thể được coi là được lấy làm mẫu từ phân bố bất đối xứng. Đồ thị hộp sửa đổi được khuyến nghị có thể xử lý vấn đề này được đưa ra trong 4.4.
VÍ DỤ: Đồ thị điểm, biểu đồ tần số, đồ thị hộp và đồ thị thân và lá của giá trị dữ liệu sau được vẽ trên Hình 3 a), 3 b), 3 c) và 3 d), tương ứng.
| 0,745 | 0,883 | 0,351 | 0,806 | 2,908 | 1,096 | 1,310 | 1,261 | 0,637 | 1,226 |
| 1,418 | 0,430 | 1,870 | 0,543 | 0,718 | 1,229 | 1,312 | 1,544 | 0,965 | 1,034 |
| 1,818 | 1,409 | 2,773 | 1,293 | 0,842 | 1,469 | 0,804 | 2,219 | 0,892 | 1,864 |
| 1,214 | 1,093 | 0,727 | 1,527 | 3,463 | 2,158 | 1,448 | 0,725 | 0,699 | 2,435 |
| 0,724 | 0,551 | 0,733 | 0,793 | 0,701 | 1,323 | 1,067 | 0,763 | 1,375 | 0,763 |
|
|
| |
| a) Đồ thị điểm của tập dữ liệu | b) Biểu đồ tần số của tập dữ liệu |
|
| Lôga chuẩn Thân và lá của tập dữ liệu N = 50 Đơn vị lá = 0,10
|
| c) Đồ thị hộp của tập dữ liệu | d) Biểu đồ thân và lá của tập dữ liệu |
CHÚ DẪN
X tập dữ liệu
Y tần suất
Hình 3 - Đồ thị tập dữ liệu
Các đồ thị này phát hiện tập dữ liệu đã cho có đuôi phải dài hơn đuôi trái. Hình 3 a), 3 b) và 3 d) chỉ ra rằng giá trị lớn nhất (3,463) thể hiện là giá trị bất thường tiềm ẩn, trong khi đồ thị hộp trên Hình 3 c) phân loại ba giá trị lớn nhất nằm phía trên rào chắn trên là các giá trị bất thường. Cột đầu tiên của hiển thị thân và lá trong Hình 3 d) được gọi là độ sâu, cột thứ hai bao gồm thân và cột thứ ba bao gồm lá. Các dòng của cột độ sâu đưa ra số đếm lá tích lũy từ trên xuống và từ dưới lên ngoại trừ dòng chứa trung vị trong ngoặc đơn. Đơn vị lá chỉ ra vị trí dấu thập phân. Đơn vị lá = 0,1 nghĩa là dấu thập phân ở trước lá, do đó số đầu tiên trong đồ thị này là 0,3, số thứ hai và thứ ba tương ứng là 0,4 và 0,5. (Ví dụ này được xem xét thêm trong 4.3.5).
4.3. Kiểm nghiệm các giá trị bất thường
4.3.1. Khái quát
Có một số lượng lớn các kiểm nghiệm giá trị bất thường (xem Tài liệu tham khảo [1]). TCVN 6910-2 (ISO 5725-2)[3] đưa ra kiểm nghiệm Grubbs và Cochran để nhận biết phòng thí nghiệm bất thường cho các kết quả kiểm nghiệm bất thường không giải thích được. Kiểm nghiệm Grubbs áp dụng cho các quan trắc riêng lẻ hoặc với trung bình của các tập dữ liệu được lấy từ phân bố chuẩn, và chỉ có thể được sử dụng để phát hiện đến hai quan trắc lớn nhất và/hoặc nhỏ nhất là giá trị bất thường trong tập dữ liệu đó. Quy trình kiểm nghiệm được nêu trong 4.3.2 phổ biến hơn, có khả năng phát hiện nhiều giá trị bất thường từ các quan trắc riêng lẻ hoặc từ trung bình của các tập dữ liệu được lấy từ phân bố chuẩn. Quy trình đề cập trong 4.3.3 và 4.3.4 có khả năng phát hiện nhiều giá trị bất thường đối với dữ liệu lấy từ phân bố hàm mũ, phân bố cực trị loại I, phân bố Weibull hoặc phân bố gamma. Cần sử dụng quy trình đưa ra trong 4.3.5 để phát hiện các giá trị bất thường trong các mẫu được coi là lấy từ tổng thể chưa biết phân bố. Quy trình kiểm nghiệm phát hiện giá trị bất thường từ tập hợp phương sai nhất định được đánh giá từ bộ mẫu nêu trong 4.3.6.
4.3.2. Mẫu từ một phân bố chuẩn
Có thể phát hiện một hoặc nhiều giá trị bất thường ở một trong hai phía của tập dữ liệu chuẩn bằng cách sử dụng quy trình được gọi là quy trình student hóa cực trị tổng quát (GESD) nhiều giá trị độ lệch bất thường (xem Tài liệu tham khảo [4]). Quy trình GESD có thể kiểm soát sai lầm loại I trong việc phát hiện nhiều hơn / giá trị bất thường ở mức ý nghĩa a khi có / giá trị bất thường trong tập dữ liệu (1 ≤ l < m), trong đó m là số lượng giá trị bất thường tối đa quy định.
Trước khi chấp nhận phương pháp phát hiện giá trị bất thường này, cần xác định rằng phần lớn dữ liệu mẫu theo phân bố chuẩn. Có thể sử dụng đồ thị xác suất chuẩn của ISO 5479[18] để kiểm nghiệm hiệu lực của giả định về tính chuẩn.
Các bước tuân thủ khi sử dụng quy trình nhiều giá trị bất thường GESD
Bước 1. Vẽ đồ thị dữ liệu mẫu đã cho x1, x2,…xn trên giấy xác suất chuẩn. Đếm số lượng điểm lệch đáng kể khỏi đường thẳng khớp với các điểm dữ liệu còn lại. Đây là số lượng giá trị bất thường nghi ngờ.
Bước 2. Chọn mức ý nghĩa a và quy định số lượng giá trị bất thường m lớn hơn hoặc bằng số giá trị bất thường nghi ngờ từ bước 1. Bắt đầu các bước sau đây với l = 0.
Bước 3. Tính thống kê kiểm nghiệm
|
| (2) |
trong đó
| I0 | biểu thị tập dữ liệu mẫu ban đầu |
| Il | biểu thị mẫu rút gọn cỡ n - 1 thu được bằng cách xóa điểm x(l-1) trong Il-1 đưa ra giá trị Rl-1; |
|
| là trung bình mẫu của mẫu Il; |
| s(Il) | Là độ lệch chuẩn của mẫu Il; |
CHÚ THÍCH 1: Đối với trường hợp khi 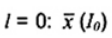 và s(I0) là trung bình mẫu và độ lệch chuẩn mẫu thu được từ mẫu ban đầu I0 = {x1, x2,…, xn} cỡ n, khi giá trị lớn nhất trong số các giá trị
và s(I0) là trung bình mẫu và độ lệch chuẩn mẫu thu được từ mẫu ban đầu I0 = {x1, x2,…, xn} cỡ n, khi giá trị lớn nhất trong số các giá trị 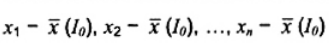 là
là 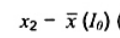 (diễn đạt), khi đó ta có
(diễn đạt), khi đó ta có 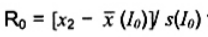 và x(0) = x2. Sau đó, I1 = I0/{x(0)} = {x1, x2,.. xn} là mẫu rút gọn cỡ n - 1 thu được bằng cách xóa giá trị dữ liệu x(0), nghĩa là x2, trong I0.
và x(0) = x2. Sau đó, I1 = I0/{x(0)} = {x1, x2,.. xn} là mẫu rút gọn cỡ n - 1 thu được bằng cách xóa giá trị dữ liệu x(0), nghĩa là x2, trong I0.
Bước 4. tính giá trị tới hạn
|
| (3) |
trong đó p = (1 - a/2)1/(n - l) và tp;v là phân vị thứ 100 của phân bố t với v bậc tự do. Lưu ý rằng nếu có thông tin bổ sung là giá trị bất thường chỉ xuất hiện trên cực trị trên hoặc cực trị dưới, thay a cho a/2 trong phương trình.
Bước 5. Lấy l = l + 1.
Bước 6. Lặp lại bước 2 đến bước 4 khi l = m.
Bước 7. Nếu R1 ≤ ll đối với tất cả l = 0, 1, 2,.., m, thì không có giá trị bất thường nào được tuyên bố. Mặt khác, các quan trắc cực trị nhất nngoài 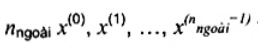 trong mẫu rút gọn thành công được tuyên bố là giá trị bất thường khi
trong mẫu rút gọn thành công được tuyên bố là giá trị bất thường khi 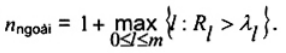
Thuật toán máy tính mô tả các bước cần thiết trong việc thực hiện quy trình nhiều giá trị bất thường GESD được nêu trong Phụ lục A.
CHÚ THÍCH 2: Kiểm nghiệm GESD tương đương với kiểm nghiệm Grubbs khi nó được dùng để kiểm nghiệm việc quan trắc bất thường nhỏ nhất hoặc lớn nhất có phải là giá trị bất thường hay không. Giá trị tới hạn của kiểm nghiệm Grubbs được đưa ra trong Bảng 5 của TCVN 6910-2:2001 (ISO 5725-2:1994)[3], và cũng có thể được tính gần đúng từ ll của bước 4 bằng cách lấy l = 0.
CHÚ THÍCH 3: Trong thực tế, số lượng giá trị bất thường m dự kiến trong mẫu cần phải nhỏ. Nếu dự kiến có nhiều quan trắc bất thường trong mẫu, thì không phải là vấn đề phát hiện giá trị bất thường và cần có các cách tiếp cận khác nhau. Tuy nhiên, m không nên quá nhỏ, nếu không sẽ có khả năng có hiệu ứng che khuất.
VÍ DỤ: Xem xét tập dữ liệu gồm 20 quan trắc.
| -2,21 | -1,84 | -0,95 | -0,91 | -0,36 | -0,19 | -0,11 | -0,10 | -0,18 | -0,30 |
| 0,43 | 0,51 | 0,64 | 0,67 | 0,93 | 1,22 | 1,35 | 1,73 | 5,80 | 12,6 |
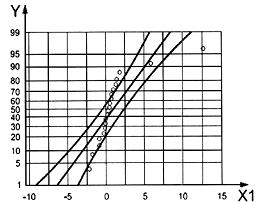
trong đó hai quan trắc sau cùng ban đầu là 0,58 và 1,26, nhưng dấu phẩy thập phân bị đặt sai vị trí. Trong việc phát hiện giá trị bất thường bằng cách sử dụng quy trình GESD, trước tiên ta phải xác nhận các quan trắc đã cho được lấy từ phân bố chuẩn. Điểm dữ liệu của đồ thị xác suất chuẩn được đưa ra trong Hình 4 a) nằm rải rác xung quanh một đường thẳng, ngoại trừ hai giá trị lớn nhất lệch rõ ràng khỏi đường thẳng. Đồ thị này cho thấy rằng tập dữ liệu, ngoại trừ hai giá trị dữ liệu cực trị có thể được giả định từ một phân bố chuẩn. Giả định này được xác nhận trên Hình 4 b) trong đó các giá trị dữ liệu, không có hai giá trị cực trị này, đều được vẽ bên trong dải 95% độ tin cậy của đồ thị xác suất chuẩn. Theo đó, ta có thể lựa chọn số lượng giá trị bất thường là m = 2 ở bước 2. Thống kê kiểm nghiệm GESD Rl và giá trị tới hạn tương ứng ll đối với l = 0, 1, 2 với mức ý nghĩa a = 0,05 được đưa ra trong bảng dưới đây.
| l | 0 | 1 | 2 |
| Rl | 3,655 9 | 3,263 4 | 2,176 1 |
| ll | 2,705 8 | 2,678 5 | 2,699 2 |
| x(l) | 12,60 | 5,80 | -2,21 |
Vì R0 = 3,655 9 > l0 = 2,705 8, R1 = 3,263 4 > l1 = 2,678 5 và R2 = 2,176 1 ≤ l2 = 2,699 2, nên ta có 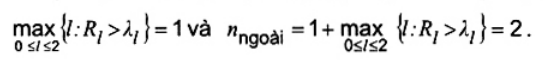
Do đó, ta công bố hai giá trị cực trị nhất x(0) = 12,60 và x(1) = 5,80 là giá trị bất thường.
CHÚ THÍCH 4: Trong ví dụ này và ví dụ sau đây, các đơn vị của quan trắc được bỏ qua vì chúng không thích hợp với các đồ thị và các kiểm nghiệm trong tiêu chuẩn này
|
|
| ||
|
| ||
| a) Đồ thị xác suất của tập dữ liệu ban đầu Chuẩn - 95 % Cl | b) Đồ thị xác suất của tập dữ liệu rút gọn Chuẩn - 95 % Cl |
CHÚ DẪN
| X1 | tập dữ liệu ban đầu |
| X2 | tập dữ liệu rút gọn |
| Y | phần trăm |
Hình 4 - Đồ thị xác suất
4.3.3. Mẫu lấy từ phân bố hàm mũ
4.3.3.1. Khái quát
Kiểm nghiệm Greenwood (xem 4.3.3.2) là kiểm nghiệm khuyến nghị cho các giá trị bất thường trong mẫu được coi là lấy từ một phân bố hàm mũ. Tuy nhiên, kiểm nghiệm này chỉ chỉ ra sự xuất hiện của các giá trị bất thường nhưng không thể nhận biết các giá trị bất thường riêng lẻ và số lượng giá trị bất thường trong mẫu. hai kiểm nghiệm liên tiếp thay thế có thể nhận biết đến m giá trị bất thường trên hoặc m giá trị bất thường dưới trong mẫu hàm mũ được đưa ra tương ứng trong 4.3.3.3 và 4.3.3.4.
4.3.3.2. Kiểm nghiệm Greenwood đối với sự có mặt của giá trị bất thường
Đây là kiểm nghiệm có hiệu lực đối với các giá trị bất thường trong mẫu được coi là lấy từ phân bố hàm mũ với hàm mật độ xác suất f(x) = l-1 exp [- (x - a) / l], x ³ a, nếu l là tham số thang đo và a là tham số vị trí hay tham số ngưỡng. Đối với mẫu hàm mũ đã cho x1, x2,…, xn cỡ n được coi như lấy từ phân bố hàm mũ với giá trị tham số đã biết a, thống kê kiểm nghiệm được đưa ra là (Tài liệu tham khảo [1]):
|
| (4) |
Giá trị GE cao đáng kể cho thấy khả năng xuất hiện một số chưa biết các giá trị bất thường là giá trị cực trị cao trong mẫu; tuy nhiên, giá trị GE thấp đáng kể cho biết sự xuất hiện các giá trị bất thường là các cực trị thấp hoặc sự kết hợp các cực trị cao và thấp. Giá trị tới hạn 2,5 % và 1 % dưới và trên gE;n của GE được cho trong Bảng B.1 đối với cỡ mẫu n lựa chọn. Đối với trường hợp khi không biết a ban đầu thì ước lượng bằng giá trị của quan trắc nhỏ nhất x(1) và khi đó giá trị tới hạn của GE là gE;n-1.
4.3.3.3. Kiểm nghiệm liên tiếp m giá trị bất thường trên có thể có
Thống kê kiểm nghiệm có thể được sử dụng để tuyên bố m quan trắc lớn nhất là các giá trị bất thường trong mẫu hàm mũ cỡ n với tham số vị trí a đã cho là (Tài liệu tham khảo [5]):
|
| (5) |
trong đó x(1) ≤ x(2) ≤ … ≤ x(n) là thống kê thứ tự của mẫu đã cho. Các giá trị lớn đáng kể của![]() cho biết các cực trị cao là giá trị bất thường. Các giá trị tới hạn trên
cho biết các cực trị cao là giá trị bất thường. Các giá trị tới hạn trên ![]() 5 % và 1 % của
5 % và 1 % của ![]() được cho trong Bảng B.2 đối với các giá trị n được chọn với m = 2, 3 và 4. Nếu
được cho trong Bảng B.2 đối với các giá trị n được chọn với m = 2, 3 và 4. Nếu ![]() tuyên bố m quan trắc lớn nhất là giá trị bất thường; nếu
tuyên bố m quan trắc lớn nhất là giá trị bất thường; nếu ![]() ≤
≤ ![]() với j = m, m - 1,…, l + 1, nhưng
với j = m, m - 1,…, l + 1, nhưng ![]() >
> ![]() tuyên bố l quan trắc nhỏ nhất là giá trị bất thường; nếu
tuyên bố l quan trắc nhỏ nhất là giá trị bất thường; nếu ![]() ≤
≤ ![]() với tất cả j = 1, 2, …, m xác nhận không có giá trị bất thường nào trong mẫu.
với tất cả j = 1, 2, …, m xác nhận không có giá trị bất thường nào trong mẫu.
Đối với trường hợp khi tham số a chưa biết, có thể được ước lượng bằng giá trị của quan trắc nhỏ nhất x(1) và giá trị tới hạn của ![]() khi đó là
khi đó là ![]() .
.
4.3.3.4. Kiểm nghiệm liên tiếp m giá trị bất thường dưới có thể có
Thống kê kiểm nghiệm có thể được sử dụng để tuyên bố m quan trắc nhỏ nhất là giá trị bất thường trong mẫu hàm mũ cỡ n với tham số vị trí a được đưa ra là (Tài liệu tham khảo [5]):
|
| (6) |
trong đó x(1) ≤ x(2) ≤ … ≤ x(n) là thống kê thứ tự của mẫu đã cho. Các giá trị lớn đáng kể của ![]() cho biết các cực trị thấp là giá trị bất thường. Các giá trị tới hạn dưới và trên 5 % và 1 %
cho biết các cực trị thấp là giá trị bất thường. Các giá trị tới hạn dưới và trên 5 % và 1 % ![]() của
của ![]() được đưa ra trong Bảng B.3 đối với các giá trị n được chọn với m = 2, 3 và 4. Nếu
được đưa ra trong Bảng B.3 đối với các giá trị n được chọn với m = 2, 3 và 4. Nếu ![]() , tuyên bố m quan trắc nhỏ nhất là giá trị bất thường; nếu
, tuyên bố m quan trắc nhỏ nhất là giá trị bất thường; nếu ![]() với j = m, m - 1, …, l + 1, nhưng
với j = m, m - 1, …, l + 1, nhưng ![]() tuyên bố l quan trắc nhỏ nhất là giá trị bất thường; nếu
tuyên bố l quan trắc nhỏ nhất là giá trị bất thường; nếu ![]() với tất cả j = 1, 2, … m xác nhận không có giá trị bất thường nào trong mẫu.
với tất cả j = 1, 2, … m xác nhận không có giá trị bất thường nào trong mẫu.
Kiểm nghiệm này chỉ có thể được sử dụng để phát hiện ra các giá trị bất thường từ các mẫu hàm mũ với tham số đã biết a. Đối với mẫu hàm mũ a chưa biết, quy trình được đề cập trong 4.4 có thể được dùng để phát hiện ra các giá trị bất thường từ dữ liệu mẫu.
VÍ DỤ: Xem xét 22 quan trắc sau đây được sắp xếp theo thứ tự tăng dần:
| 10,10 | 10,27 | 10,85 | 11,38 | 12,85 | 13,13 | 14,07 | 14,26 | 14,51 | 14,55 | 15,73 |
| 17,43 | 17,72 | 18,49 | 20,75 | 21,37 | 22,50 | 24,22 | 25,61 | 33,84 | 43,00 | 84,94 |
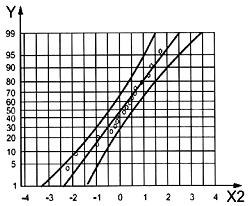
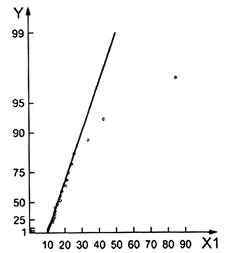
Trong việc phát hiện các giá trị bất thường bằng cách sử dụng thống kê Greenwood, bước đầu tiên là xác nhận các quan trắc đã cho được coi như lấy từ phân bố hàm mũ. Các điểm dữ liệu của đồ thị xác suất hàm mũ được đưa ra trong Hình 5 a) xuất hiện nằm rải rác quanh một đường thẳng, ngoại trừ giá trị lớn nhất hoặc hai giá trị lớn nhất. Đồ thị này cho thấy rằng tập dữ liệu, ngoại trừ một hoặc hai dữ liệu cực trị, có thể được giả định từ một phân bố hàm mũ. Giả định này được xác nhận trong Hình 5 b) trong đó giá trị dữ liệu, không có hai giá trị lớn nhất, phân tán quanh một đường thẳng. Với tham số vị trí ước lượng a = 10,10, thống kê Greenwood là GE = 8 386,326/(249,37)2 = 0,134 86. Từ Bảng B.1, giá trị tới hạn dưới và trên 2,5 % gE;21 của GE tương ứng là 0,067 3 và 0,133 8. Do đó, giá trị GE 0,134 86 tính được nằm trên giá trị tới hạn trên 0,133 8 và ta kết luận rằng một hay nhiều cực trị cao trong tập dữ liệu đã cho là các giá trị bất thường.
Khi các điểm dữ liệu nghi ngờ là hai cực trị cao, có thể sử dụng kiểm nghiệm ở 4.3.3.3 để kiểm nghiệm hai giá trị bất thường có thể trong mẫu. Lấy m = 2, ta có ![]() và
và ![]() . Sau khi so sánh những giá trị này với giá trị tới hạn tương ứng của
. Sau khi so sánh những giá trị này với giá trị tới hạn tương ứng của ![]() và
và ![]() được lấy từ Bảng B.2 với a = 0,05, chỉ giá trị lớn nhất (84,94) mới được biểu thị như là một giá trị bất thường với mức ý nghĩa 5 %.
được lấy từ Bảng B.2 với a = 0,05, chỉ giá trị lớn nhất (84,94) mới được biểu thị như là một giá trị bất thường với mức ý nghĩa 5 %.
|
|
|
| a) Đồ thị xác suất hàm mũ của tập dữ liệu ban đầu | b) Đồ thị xác suất hàm mũ của tập dữ liệu rút gọn |
CHÚ DẪN:
| X1 | tập dữ liệu ban đầu |
| X2 | tập dữ liệu rút gọn |
| Y | Xác suất hàm mũ |
Hình 5 - Đồ thị xác suất hàm mũ
4.3.4. Mẫu lấy từ một số phân bố không chuẩn đã biết
4.3.4.1. Khái quát
Việc phát hiện các giá trị bất thường trong mẫu được lấy từ những phân bố không chuẩn có tầm quan trọng đáng kể trong thực tế. Các giá trị bất thường trong mẫu hàm mũ và mẫu gamma xuất hiện trong nghiên cứu về kiểm nghiệm tuổi thọ, giao thông và dòng chảy sông, v.v…, trong khi mẫu cực trị xuất hiện trong nghiên cứu về các giá trị, như tốc độ gió tối đa hoặc các thành tích thể thao. Phân bố lôga chuẩn và Weibull thường xuất hiện trong các ứng dụng về độ tin cậy. Trong trường hợp họ phân bố không chuẩn đã biết và là phân bố lôga chuẩn, phân bố cực trị, phân bố Weibull hoặc phân bố gamma, các phép biến đổi dưới đây được khuyến nghị để biến đổi dữ liệu giống như phân bố được yêu cầu.
4.3.4.2. Đối với mẫu dữ liệu x1, x2,.., xn được xem là lấy từ phân bố lôga chuẩn với hàm mật độ.
![]()
các giá trị chuyển đổi ln x1, ln x2,…, ln xn là mẫu từ phân bố chuẩn với trung bình m và phương sai s2. Sau đó có thể sử dụng quy trình kiểm nghiệm của 4.3.2 và/hoặc 4.4 để phát hiện các giá trị bất thường trong số các giá trị chuyển đổi.
4.3.4.3. Đối với mẫu dữ liệu x1, x2,… xn được lấy từ phân bố cực trị loại 1 với hàm phân bố
P(X ≤ x) = exp {-exp[- (x - a)/b]}, -¥ < x < ¥
các giá trị mẫu chuyển đổi exp(-x1/b), exp(-x2/b),…, exp(-xn/b), theo phân bố hàm mũ với trung bình exp(-a/b). Sau đó có thể sử dụng quy trình kiểm nghiệm của 4.3.3 và/hoặc 4.4 để phát hiện các giá trị bất thường trong số các giá trị chuyển đổi.
4.3.4.4. Đối với mẫu dữ liệu x1, x2,…, xn được lấy từ phân bố Weibull với hàm phân bố
![]() , x > a, b > 0, r > 0
, x > a, b > 0, r > 0
giá trị mẫu chuyển đổi (x1 - a)r, (x2 - a)r, …,(xn - a)r theo phân bố hàm mũ có trung bình br. Sau đó có thể sử dụng quy trình kiểm nghiệm trong 4.3.2 và/hoặc 4.4 để phát hiện các giá trị bất thường trong số các giá trị chuyển đổi.
CHÚ THÍCH: Có thể chuyển đổi dữ liệu phân bố hàm mũ x thành ![]() để đưa ra dữ liệu phân bố chuẩn gần đúng [6].
để đưa ra dữ liệu phân bố chuẩn gần đúng [6].
4.3.4.5. Đối với mẫu dữ liệu x1, x2,…, xn được coi là lấy từ phân bố gamma với hàm mật độ xác suất
f(x) = [brG(r)]-1 xr-1 exp(-x/b), x > 0, b >0
giá trị chuyển đổi ![]() gần như tuân theo phân bố chuẩn. Sau đó có thể sử dụng quy trình kiểm nghiệm trong 4.3.2 và/hoặc 4.4 để phát hiện các giá trị bất thường trong số các giá trị chuyển đổi.
gần như tuân theo phân bố chuẩn. Sau đó có thể sử dụng quy trình kiểm nghiệm trong 4.3.2 và/hoặc 4.4 để phát hiện các giá trị bất thường trong số các giá trị chuyển đổi.
4.3.5. Mẫu lấy từ phân bố chưa biết
Khi việc phát hiện các giá trị bất thường trong mẫu được coi là lấy từ tổng thể với phân bố chưa biết và phân bố bất đối xứng, phương pháp tổng quát là chuyển đổi dữ liệu không chuẩn thành giống như phân bố chuẩn. Sau đó có thể ứng dụng các kiểm nghiệm giá trị bất thường ở 4.3.3. đối với mẫu chuẩn cho mẫu chuyển đổi. Hai phương pháp được sử dụng rộng rãi là chuyển đổi Box-Cox và chuyển đổi Johnson. Họ chuyển đổi lũy thừa Box-Cox có dạng [7].
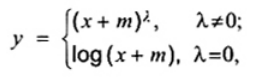
trong đó
nếu l ¹ 0, tham số m được chọn sao cho x + m dương, và
nếu l = 0, tham số m được đặt bằng không để đảm bảo rằng dữ liệu ban đầu x giữ nguyên không đổi.
Lựa chọn tối ưu tham số chuyển đổi l được cung cấp tự động trong một số phần mềm thống kê.
Chuyển đổi Johnson chuyển đổi dữ liệu thành giống với phân bố chuẩn bằng cách sử dụng họ phân bố Johnson[8].
CHÚ THÍCH 1: Chuyển đổi lũy thừa Box-Cox và chuyển đổi Johnson có sẵn trong các phần mềm thống kê liên quan.
CHÚ THÍCH 2: Chuyển đổi Box-Cox đơn giản và dễ hiểu. Tuy nhiên, hệ chuyển đổi Johnson có thể phù hợp với dữ liệu có các giá trị âm.
VÍ DỤ: Xem xét tập dữ liệu trong 4.2 được lấy từ thống kê với phân bố chưa biết. Đồ thị điểm, biểu đồ tần số, đồ thị hộp và đồ thị thân và lá (trên Hình 3) chỉ ra rằng dữ liệu được lấy từ phân bố bất đối xứng. Cần chuyển đổi dữ liệu để biến đổi giá trị dữ liệu thành giống với phân bố chuẩn. Đồ thị Box-Cox và đồ thị xác suất của tập dữ liệu được cho trên Hình 6 và 7 có được từ một phần mềm thống kê sẵn có. Hình 6 bao gồm giá trị l ước lượng của -0,19, và giá trị l làm tròn 0,00 là giá trị được sử dụng trong phép chuyển đổi. Hình này cũng bao gồm giới hạn tin cậy dưới 95% của -0,77 và giới hạn tin cậy trên là 0,36 được đánh dấu trên đồ thị bằng đường thẳng đứng. Trong tình huống thực tế, giá trị của l tương ứng với phép chuyển đổi thông thường, như căn bậc hai (l = 0,5) hoặc loga tự nhiên (l = 0) nên được sử dụng. Trong ví dụ này, lấy giá trị của l bằng “không” là lựa chọn hợp lý vì nó nằm trong khoảng tin cậy 95 %. Do đó, chuyển đổi loga tự nhiên có thể được ưu tiên hơn đối với phép chuyển đổi được xác định bởi ước lượng l tốt nhất. Các đồ thị xác suất của dữ liệu ban đầu và dữ liệu chuyển đổi được đưa ra trên Hình 7. p giá trị là 0,318 được đưa ra trên Hình 7(b), được đánh giá từ thống kê kiểm nghiệm Anderson-Darling, chỉ ra rằng dữ liệu chuyển đổi giống với phân bố chuẩn
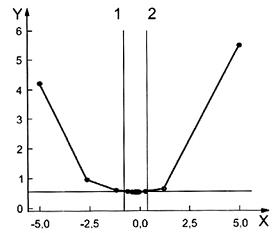
| Lambda (sử dụng 95,0 % độ tin cậy) | |
| Ước lượng Giới hạn mức tin cậy dưới Giới hạn mức tin cậy trên Giá trị được làm tròn | -0,19 -0,77 0,36 0,00 |
CHÚ DẪN
| X lambda | 1 giới hạn tin cậy dưới |
| Y độ lệch chuẩn | 2 giới hạn tin cậy trên |
Hình 6 - Đồ thị Box-Cox của tập dữ liệu
|
|
| ||||
|
| ||||
| a) Đồ thị xác suất của dữ liệu ban đầu | b) Đồ thị xác suất của dữ liệu chuyển đổi |
Hình 7 - Đồ thị xác suất của dữ liệu ban đầu và dữ liệu chuyển đổi
4.3.6. Kiểm nghiệm Cochran đối với phương sai bất thường
Rất quan trọng để phát hiện ra các giá trị bất thường từ tập hợp các phương sai nhất định được đánh giá từ tập hợp dữ liệu mẫu, đặc biệt trong việc ước lượng độ chính xác của các phương pháp đo [3] bằng thực nghiệm hợp tác liên phòng thí nghiệm. Kiểm nghiệm Cochran được sử dụng rộng rãi cho việc xác định giá trị phương sai lớn nhất trong một tập hợp phương sai đã cho có lớn hơn đáng kể so với các phương sai còn lại hay không.
Cho tập hợp p phương sai ![]() được tính từ p mẫu, mỗi mẫu cỡ n, thống kê kiểm nghiệm Cochran được cho bởi
được tính từ p mẫu, mỗi mẫu cỡ n, thống kê kiểm nghiệm Cochran được cho bởi
|
| (7) |
trong đó ![]() là phương sai lớn nhất trong tập hợp phương sai p.
là phương sai lớn nhất trong tập hợp phương sai p.
Giá trị tới hạn 5 %, 1 % và 0,1 % của thống kê kiểm nghiệm C được cho trong các bảng của Phụ lục E đối với các phương sai mẫu p = 2(1)40 1) được đánh giá từ p mẫu, mỗi mẫu cỡ n = 2(1)10. Khi đó, phương sai lớn nhất được xác định là giá trị bất thường nếu giá trị tính toán của C vượt quá giá trị tới hạn.
CHÚ THÍCH: Giá trị tới hạn của kiểm nghiệm Cochran được cho trong Phụ lục E chỉ nên được áp dụng khi tất cả độ lệch chuẩn thu được từ cùng một số (n) kết quả kiểm nghiệm.
VÍ DỤ: Năm phòng thí nghiệm tham gia vào thí nghiệm để xác định sự hấp thụ độ ẩm trong cốt bê tông. Thu được tám kết quả kiểm nghiệm trong các điều kiện lặp lại và theo phương pháp đo chuẩn của từng phòng thí nghiệm. Tập hợp phương sai thu được là
| Phòng thí nghiệm, i | 1 | 2 | 3 | 4 | 5 |
| Phương sai, | 12,134 | 2,303 | 3,594 | 3,319 | 3,455 |
Từ bảng E.1, giá trị tới hạn 5 % của kiểm nghiệm Cochran đối với số phòng thí nghiệm p = 5 và n = 8 phép lặp là 0,456 4. Vì giá trị thống kê kiểm nghiệm Cochran C = 12,134/(12,134 + 2,303 + 3,594 + 3,319 + 3,455) = 0,489 2 vượt quá giá trị tới hạn, nên ta kết luận rằng phương sai phòng thí nghiệm 1 có thể được coi là lớn hơn đáng kể so với số còn lại.
4.4. Kiểm nghiệm giá trị bất thường bằng đồ thị
Khuyến nghị đồ thị hộp sửa đổi dưới đây đối với việc phát hiện giá trị bất thường khi phân bố tổng thể của tập dữ liệu nhất định được giả định là theo phân bố chuẩn hoặc phân bố hàm mũ. Không giống như quy trình kiểm nghiệm giả thuyết của 4.3, kiểm nghiệm giá trị bất thường bằng đồ thị này dựa trên đồ thị hộp không có yêu cầu biết trước về số giá trị bất thường hoặc hướng giá trị bất thường được định vị.
Phần tư dưới và trên xL;n và xU;n được sử dụng thay cho tứ phân vị thứ nhất và thứ ba Q1 và Q3 trong việc đánh giá rào chắn dưới LF và rào chắn trên UF của đồ thị hộp sửa đổi cụ thể theo phân bố này, nghĩa là
| LF = xL:n - kL (xU:n - xL:n) UF = xU:n - kU (xU:n - xL:n) | (8) |
trong đó
| n | là cỡ mẫu | |
| kL và kU | là các giá trị phụ thuộc vào phân bố phổ biến của tổng thể giả thuyết và cỡ mẫu n; | |
| xL:n | là phần tư dưới của đồ thị hộp đánh giá là | |
|
| Nếu f = 0 Nếu f > 0 | |
xU:n là phần tư trên của đồ thị hộp đánh giá là
|
| Nếu f = 0 Nếu f > 0 |
trong đó n/4 = i + f khi i là phần tích của n/4 và f là phần phân số của n/4, và x(1) ≤ x(2 ) ≤ … ≤ x(n) là thống kê thứ tự từ mẫu.
CHÚ THÍCH 1: Định nghĩa này về phần tư dưới và trên được sử dụng để xác định các giá trị kL và kU khuyến nghị nêu trong Phụ lục C và là giá trị mặc định hoặc tùy chọn trong một số phần mềm thống kê được sử dụng rộng rãi.
Các quan trắc nằm trên rào chắn trên hoặc nằm dưới rào chắn dưới được gán là những giá trị bất thường tiềm năng. Đặc điểm nổi bật của đồ thị hộp sửa đổi là giá trị không đổi kL và kU được xác định từ yêu cầu đối với mẫu không có giá trị bất thường và tỷ lệ ngoài trên mỗi mẫu, nghĩa là xác suất một hoặc nhiều quan trắc trong mẫu sẽ bị phân loại sai là giá trị bất thường, bằng với một giá trị a nhỏ nhất định. Đồ thị hộp sửa đổi này rút gọn đồ thị hộp cổ điển đề cập trong 4.2 khi kL = kU = 1,5. Có thể xác định giá trị của kL và kU từ phương trình (C.2) trong Phụ lục C đối với các mẫu lấy từ phân bố chuẩn và phân bố hàm mũ đối với giá trị lựa chọn a khi 9 ≤ n ≤ 500.
CHÚ THÍCH 2: Rào chắn dưới của đồ thị hộp sửa đổi được thiết lập theo giả định phân bố hàm mũ có thể có giá trị âm nếu tập dữ liệu cho trước không theo sát phân bố hàm mũ.
VÍ DỤ 1: Từ n = 20 quan trắc của ví dụ trong 4.3.2, ta có n/4 = 20/4 = 5 dẫn đến i = 5 và f = 0. Như vậy, phần tư dưới và trên của đồ thị hộp được đánh giá là
xL:n = [x(5) + x(6)]/2 = 0,5 (-0,36 - 0,19) = -0,275
và
xU:n = [x(15) + x(16)]/2 = 0,5 (-0,93 - 1,22) = -1,075
Đối với mẫu chuẩn, rào chắn trên và dưới của đồ thị hộp với một số tỷ lệ ngoại vi cho mỗi mẫu a = 0,05 được thiết lập bằng cách sử dụng kL = kU = 2,238 2 (minh họa trong ví dụ 1 của Phụ lục C)
LF = xL:n - kL (xU:n - xL:n) = -0,275 - 2,238 2 (1,075 + 0,275) = -3,297
UF = xU:n - kU (xU:n - xL:n) = 1,075 + 2,238 2 (1,075 + 0,275) = 4,097
Do đó, hai cực trị lớn hơn 5,80 và 12,60 nằm trên rào chắn trên được công bố là giá trị bất thường.
VÍ DỤ 2: Từ n = 22 quan trắc mẫu trong 4.3.3.4, ta có n/4 = 22/4 = 5 + 1/2, do đó phần tư dưới và trên của đồ thị hộp được đánh giá là
xL:n = x(6) = 13,13 và xU:n = x(17) = 22,50
Đối với mẫu hàm mũ, rào chắn trên và rào chắn dưới của đồ thị hộp với một tỷ lệ ngoại vi a = 0,05 được tính là
LF = xL:n - kL (xU:n - xL:n) = 13,13 - 0,665 0 (22,50 - 13,13) = 6,899
UF = xU:n - kU (xU:n - xL:n) = 22,50 + 6,231 3 (22,50 - 13,13) = 80,887
Do đó, cực trị 84,94 nằm trên rào chắn trên được công bố là giá trị bất thường. Tìm được giá trị của kL = 0,665 0 và kU = 6,231 3 từ Phụ lục C, ví dụ 2.
VÍ DỤ 3: Giả sử giá trị lớn thứ hai 43,0 trong ví dụ ở 4.3.3.4 bị ghi sai là 4,30. Vì giá trị 4,30 nằm dưới rào chắn dưới LF = 6,899 của đồ thị hộp nên nó được công bố là giá trị bất thường. Tuy nhiên, do hiệu ứng che khuất của cực trị 4,30 và 84,94, các quy trình kiểm nghiệm chính thức của 4.3 không những không có khả năng phát hiện giá trị 4,30 là giá trị bất thường, mà còn không phát hiện được giá trị lớn nhất 84,94 là giá trị bất thường.
5. Thỏa hiệp giá trị bất thường trong dữ liệu đơn biến
5.1. Phân tích dữ liệu ổn định
Bất kỳ giá trị bất thường nào phát hiện cần được nghiên cứu để giải thích. Nếu do sai lỗi có thể tìm được nguyên nhân gây ra (ví dụ lỗi ghi chép, lỗi pha loãng, sai số đo,…), thì giá trị của nó cần được hiệu chỉnh hoặc xóa bỏ nếu không biết giá trị thực. Nếu sự xuất hiện của các giá trị bất thường không được giải thích hợp lý thì không nên loại bỏ; chúng cần được xử lý như các quan trắc hợp lệ và sử dụng trong phân tích dữ liệu tiếp theo bằng cách sử dụng các quy trình ổn định có khả năng chịu ảnh hưởng của các giá trị bất thường. Các phương pháp thỏa hiệp giá trị bất thường của 5.2 và 5.3 có thể làm giảm ảnh hưởng của các quan trắc bất thường đến các kết quả phân tích dữ liệu mà không cần bỏ chúng. Một lựa chọn khác là tiến hành phân tích khi có và không có giá trị bất thường.
5.2. Ước lượng ổn định vị trí
5.2.1. Khái quát
Trung bình mẫu là ước lượng tối ưu của vị trí trung tâm đối với dữ liệu chuẩn. Tuy nhiên, nó không phải là ước lượng bền và ổn định của vị trí trung tâm. Có nhiều phương pháp ước lượng ổn định về vị trí đã được đưa ra trong tài liệu. Trung bình đã cắt tỉa đưa ra trong 5.2.2 được sử dụng rộng rãi để giảm bớt sự biến dạng gây ra do các quan trắc bất thường khi ước lượng vị trí trung tâm từ các mẫu lấy từ phân bố tổng thể đối xứng. Đối với những mẫu được lấy từ phân bố tổng thể bất đối xứng, khuyến nghị hàm ước lượng vị trí mô tả trong 5.2.3.
5.2.2. Trung bình đã cắt tỉa
Khi phát hiện các giá trị bất thường có thể trong các mẫu được lấy từ phân bố tổng thể đối xứng, khuyến nghị dùng trung bình đã cắt tỉa để ước lượng trung tâm của phân bố đối xứng.
Lấy x(1) ≤ x(2) ≤ … ≤ x(n) là thống kê thứ tự từ mẫu cỡ n.
Lấy r = [an] biểu thị số nguyên lớn nhất nhỏ hơn hoặc bằng an và g = an - r là phần phân số của an, trong đó 0 ≤ a ≤ 0,5 là tỷ lệ các quan trắc bất thường trong tập dữ liệu.
Trung bình đã cắt tỉa a[9] biểu thị rằng ![]() , được tính bằng cách bỏ qua r quan trắc nhỏ nhất và r quan trắc lớn nhất của mẫu đã cho, gán cho cả hai quan trắc giữ lại gần nhất x(r + 1) và x(n - r) một trọng số rút gọn (1 - g), nghĩa là
, được tính bằng cách bỏ qua r quan trắc nhỏ nhất và r quan trắc lớn nhất của mẫu đã cho, gán cho cả hai quan trắc giữ lại gần nhất x(r + 1) và x(n - r) một trọng số rút gọn (1 - g), nghĩa là
![]()
CHÚ THÍCH 1: Khi an là số nguyên, ta có g = 0, do đó trung bình đã cắt tỉa a là trung bình mẫu của mẫu đã cắt tỉa.
CHÚ THÍCH 2: Giá trị a quy định trước thường được lấy nhỏ hơn 0,25. Trung bình mẫu truyền thống là trung bình đã cắt tỉa 0, trong khi trung vị mẫu xấp xỉ là trung bình đã cắt tỉa 0,5.
CHÚ THÍCH 3: Trung bình Winsori hóa a là một thay thế phổ biến khác trong đó r = [an] quan trắc nhỏ nhất được rút gọn để từng quan trắc có giá trị x(r + 1) và r quan trắc lớn nhất của tập dữ liệu được rút gọn để nhận giá trị x(n - r), nghĩa là thay thế (1 - g) của ![]() bằng giá trị r.
bằng giá trị r.
VÍ DỤ: Đối với tập dữ liệu n = 20 quan trắc nêu trong 4.3.2, ta tính trung bình, trung vị, trung bình đã cắt tỉa 5 %, 10 %, 15 %, 18 % và 20 %. Những giá trị này là
Trung bình = ![]()
Trung bình = ![]()
![]()
![]()
![]()
![]()
![]()
Những kết quả này cho thấy trung bình mẫu tương đối lớn là do sự có mặt của hai giá trị bất thường, trong khi các trung bình đã cắt tỉa thì ổn định sau khi 10 % đến 20 % dữ liệu đã được cắt tỉa.
5.2.3. Ước lượng vị trí sử dụng trọng số kép
Ước lượng vị trí trọng số kép[9] được dùng khi có mặt các giá trị bất thường đối với các mẫu lấy từ phân bố bất đối xứng và ổn định đối với sai lệch nhỏ so với các giả định tính chuẩn. Cho mẫu x1, x2,...xn cỡ n, ước lượng vị trí trọng số kép có thể thu được là
|
| (10) |
trong đó ui = (xi - Tn) / cMad, với c = 6,0, Mad = Trung vị (|xi - M|, i = 1, 2,..., n) và M là trung vị mẫu. Ước lượng của Tn cần được tính toán lặp lại. Lấy ![]() và
và 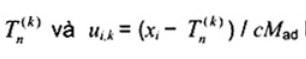 là ước lượng của Tn và ui ở lần lặp thứ k, ước lượng của Tn tại lần lặp thứ (k + 1) là
là ước lượng của Tn và ui ở lần lặp thứ k, ước lượng của Tn tại lần lặp thứ (k + 1) là
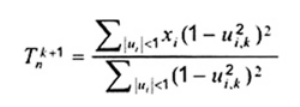
Phép tính lặp này cần tiếp tục cho đến khi chuỗi ước lượng hội tụ với độ chính xác mong muốn. Ví dụ, có thể kết thúc các phép lặp nếu 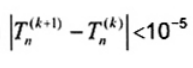 (chẳng hạn). Giá trị bắt đầu thích hợp
(chẳng hạn). Giá trị bắt đầu thích hợp ![]() là trung vị mẫu M.
là trung vị mẫu M.
CHÚ THÍCH: Theo giả định tính chuẩn, ước lượng trọng số kép với c = 6,0 ngụ ý rằng các quan trắc cách trung vị một khoảng lớn hơn bốn độ lệch chuẩn sẽ được cho trọng số bằng không.
VÍ DỤ: Ước lượng vị trí trọng số kép của tập dữ liệu đã cho trong 4.3.2 là Tn = 0,176 9. Giá trị này gần với giá trị trung bình (0,156 5) của tập dữ liệu với hai cực trị (5,80 và 12,8) được thay thế bằng giá trị đúng của chúng (0,58 và 1,28).
5.3. Ước lượng ổn định của độ phân tán
5.3.1. Khái quát
Hai trong số các hàm ước lượng thang đo được sử dụng rộng rãi là có khả năng chịu được các quan trắc bất thường và có thể được sử dụng thay cho độ lệch chuẩn mẫu được đưa ra dưới đây.
5.3.2. Độ lệch tuyệt đối kép trung vị - trung vị
| Sn = sn Trung vị, (Trung vị, |xi - xj|, i ¹ j, i, j = 1, 2, … n | (11) |
Hằng số sn là hệ số hiệu chỉnh được chọn để đảm bảo rằng Sn là hàm ước lượng không chệch đối với tham số thang đo của phân bố giả thuyết (chuẩn, hàm mũ, v.v...). Đối với mẫu chuẩn lớn, giá trị của sn được lấy là 1,192 6 (xem Tài liệu tham khảo [10]), trong khi sn = 1,698 2 đối với mẫu hàm mũ lớn. Giá trị của sn cho trong Bảng D.1 đối với mẫu chuẩn cỡ n = 2(1)20(10)100, 120, 150, 200, 300 và 500.
5.3.3. Ước lượng thang đo trọng số kép
Ước lượng thang đo trọng số kép trong mẫu x1, x2,..., xn cùng thảo luận trong Tài liệu tham khảo [9], và có thể thu được là
| | (12) |
trong đó M là trung vị mẫu, ui = (xi - M) / (cMad) và Mad = Trung vị (|xi - M|, i = 1, 2,... n) đối với mẫu chuẩn cỡ n. Lựa chọn được khuyến nghị với c là giá trị 9,0. Giá trị của sbi dựa trên c = 9,0 được cho trong Bảng D.1 đối với mẫu chuẩn cỡ n = 2(1)20(10)100, 120, 150, 200, 300 và 500.
CHÚ THÍCH: Theo giả định chuẩn, hàm ước lượng trọng số kép với c = 9,0 cho trọng số bằng không đối với các quan trắc cách trung vị một khoảng lớn hơn 6 độ lệch chuẩn.
VÍ DỤ: Đối với tập dữ liệu cho trong 4.3.2, độ lệch chuẩn mẫu cổ điển s, ước lượng thang đo ổn định S của 5.3.2 và Sbi của 5.3.3 được cho bởi
s = 3,177 2, Sn = 1,015 0, Sbi = 1,156 5
Những kết quả này cho thấy rõ rằng độ lệch chuẩn mẫu cổ điển (s) đã tăng lên nhiều bởi hai quan trắc lớn. Hai ước lượng ổn định tương ứng Sn và Sbi có giá trị tương đối nhỏ và gần nhau.
6. Giá trị bất thường trong dữ liệu đa biến và hồi quy
6.1. Khái quát
Các giá trị bất thường trong dữ liệu đa biến và hồi quy khó nhận biết hơn so với trong dữ liệu đơn biến. Giá trị bất thường đa biến không cần là một giá trị bất thường trong bất kỳ thành phần nào của nó hay tọa độ hai biến số. Giá trị bất thường đa biến cũng có thể bị che giấu ở mức độ nhất định bởi cấu trúc chung của cơ chế tạo ra chúng và sự có mặt của chúng chỉ thấy được sau khi mô hình hóa được cấu trúc của dữ liệu. Giá trị bất thường trong dữ liệu hồi quy không thể là cực trị đơn mà là một quan trắc sai lệch đáng kể so với dạng thức chung của mô hình hồi quy.
6.2. Giá trị bất thường trong dữ liệu đa biến
Ý tưởng chung đằng sau các phương pháp nhận biết các giá trị bất thường từ dữ liệu đa biến chuyển đổi các quan trắc đa biến thành thống kê đơn biến. Thống kê được sử dụng rộng rãi là khoảng cách Mahalanobis, đo khoảng cách của quan trắc đa biến với trung bình mẫu của tập dữ liệu, được tiêu chuẩn hóa bằng ma trận phương sai mẫu. Giả sử ta có p biến, cho bởi X1, X2,… Xp được sắp xếp theo vectơ p thành phần X = (X1, X2, … XP)T.
Lấy m = (m1, m2, … mp)T là vectơ của trung bình p biến mẫu nghiên trong X, lấy phương sai và hiệp phương sai của biến ngẫu nhiên trong X ký hiệu bằng một ma trận hiệp phương sai S cấp p x p trong đó các thành phần đường chéo chính của S là phương sai và các thành phần ngoài đường chéo là hiệp phương sai của các biến X trong X.
Khoảng cách Mahalanobis từ X tới m được xác định là
|
| (13) |
Có thể phát hiện các giá trị bất thường đối với mẫu gồm n quan trắc đa biến x1, x2, … xn từ n khoảng cách Mahalanobis tương ứng ![]() , i = 1, 2,…n. Đối với trường hợp khi vectơ X theo phân bố chuẩn đa biến với trung bình m và ma trận hiệp phương sai S, khoảng cách Mahalanobis bình phương,
, i = 1, 2,…n. Đối với trường hợp khi vectơ X theo phân bố chuẩn đa biến với trung bình m và ma trận hiệp phương sai S, khoảng cách Mahalanobis bình phương, ![]() , được biết là tuân theo phân bố khi bình phương p bậc tự do.
, được biết là tuân theo phân bố khi bình phương p bậc tự do.
Việc tính toán khoảng cách Mahalanobis ở trên phụ thuộc vào sự hiểu biết về m và S. Trong thực tế, thường cần ước lượng giá trị của m và S từ dữ liệu mẫu. Khi có các giá trị bất thường, ước lượng ổn định m và S cần thu được bằng hàm ước lượng[11] định thức hiệp phương sai tối thiểu (MCD). Phương pháp MCD tìm kiếm tập hợp h quan trắc trong số n quan trắc đã cho dẫn đến ma trận hiệp phương sai có định thức nhỏ nhất có thể. Nếu tập dữ liệu được giả định chứa tối đa 100a % quan trắc bất thường thì giá trị của h cần được lấy gần với (1 - a)n; tuy nhiên, cần lớn hơn giá trị nguyên [(n + p + 1)/2]. Giá trị trung bình và ma trận hiệp phương sai h này tương ứng là ước lượng MCD mMCD và SMCD của m và S. Khi đó khoảng cách ổn định của quan trắc xi được xác định là
|
| (14) |
Theo giả định tính chuẩn đa biến, chuẩn mực bảo toàn[11] là để công bố các quan trắc có khoảng cách ổn định lớn hơn giá trị ngưỡng 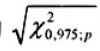 là các giá trị bất thường, trong đó
là các giá trị bất thường, trong đó 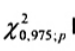 là phân vị 97,5 % của phân bố khi-bình phương với p bậc tự do.
là phân vị 97,5 % của phân bố khi-bình phương với p bậc tự do.
So sánh trực quan giữa khoảng cách Mahalanobis và khoảng cách ổn định, và hiệu lực của việc sử dụng khoảng cách ổn định trong việc phát hiện các giá trị bất thường, được đưa ra trong ví dụ sau đây.
VÍ DỤ: Tập hợp 35 quan trắc hai biến (x1, x2) thu thập từ một thực nghiệm được ghi lại như sau:
| Số dữ liệu i | x1i | x2i | Số dữ liệu i | x1i | x2i | Số dữ liệu i | x1i | x2i |
| 1 2 3 4 5 6 7 8 9 10 11 12 | 12,00 9,30 15,00 10,15 10,45 17,45 10,80 10,80 10,75 17,00 8,25 12,66 | 12,60 10,20 14,50 19,30 10,80 16,90 11,95 10,85 11,65 17,50 17,20 13,30 | 13 14 15 16 17 18 19 20 21 22 23 24 | 12,90 12,90 13,10 16,00 13,45 13,55 14,30 14,40 13,60 14,80 10,15 15,10 | 12,95 13,50 13,80 16,25 13,00 15,20 15,10 14,55 14,35 14,99 9,90 15,15 | 25 26 27 28 29 30 31 32 33 34 35 | 15,60 13,25 16,83 12,00 17,30 10,65 17,55 18,20 19,10 13,55 12,55 | 15,64 12,85 16,85 11,70 17,25 10,80 17,70 18,35 19,30 14,00 15,10 |
Khoảng cách Mahalanobis và khoảng cách ổn định của từng quan trắc được tính toán và được vẽ trên Hình 8 bằng cách sử dụng h = 32 quan trắc để tính toán ước lượng MCD. Hình này được vẽ bằng cách sử dụng phần mềm mã nguồn mở LIBRA[11]. Đường kẻ đứt nét là tập hợp các điểm trong đó khoảng cách ổn định bằng khoảng cách Mahalanobis. Đường nằm ngang và dọc được lấy từ giá trị ngưỡng ![]() . Điểm nằm ngoài đường kẻ này có thể được biểu thị là giá trị bất thường. Khoảng cách ổn định trong đồ thị này cho thấy các điểm 4, 11 và 35 là các giá trị bất thường. Tuy nhiên, chỉ điểm 4 và 11 được công bố là giá trị bất thường khi sử dụng khoảng cách Mahalanobis. Có thể xem như ví dụ về hiệu ứng che khuất xác định trong 2.3 rằng khoảng cách Mahalanobis chỉ công bố quan trắc 4 và 11 là giá trị bất thường. Nếu khoảng cách Mahalanobis được tính không sử dụng các quan trắc 4 và 11, thì quan trắc 35 cũng được công bố là giá trị bất thường.
. Điểm nằm ngoài đường kẻ này có thể được biểu thị là giá trị bất thường. Khoảng cách ổn định trong đồ thị này cho thấy các điểm 4, 11 và 35 là các giá trị bất thường. Tuy nhiên, chỉ điểm 4 và 11 được công bố là giá trị bất thường khi sử dụng khoảng cách Mahalanobis. Có thể xem như ví dụ về hiệu ứng che khuất xác định trong 2.3 rằng khoảng cách Mahalanobis chỉ công bố quan trắc 4 và 11 là giá trị bất thường. Nếu khoảng cách Mahalanobis được tính không sử dụng các quan trắc 4 và 11, thì quan trắc 35 cũng được công bố là giá trị bất thường.
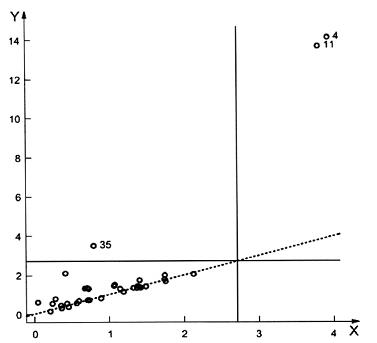
CHÚ DẪN
X khoảng cách Mahalanobis
Y khoảng cách ổn định
Dữ liệu được vẽ trên Hình 11 trong đó các điểm 4, 11 và 35 được đánh dấu.
Hình 8 - Đồ thị khoảng cách Mahalanobis theo khoảng cách ổn định của tập dữ liệu
6.3. Giá trị bất thường trong hồi quy tuyến tính
6.3.1. Khái quát
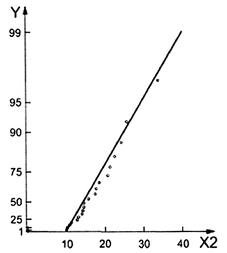
Trong phân tích hồi quy tuyến tính đơn, điểm dữ liệu (Y, X) có thể là bất thường so với giá trị Y, giá trị X của nó hoặc cả hai. Trong biểu đồ phân tán (yi, xi) đưa ra trên Hình 9, điểm 1 là bất thường so với giá trị y của của nó vì nằm xa ngoài phân tán, mặc dù giá trị x của nó không phải là giá trị bất thường, điểm 3 là bất thường so với giá trị x của nó vì giá trị x này lớn hơn giá trị của các điểm khác và giá trị y không phải là giá trị bất thường; điểm 2 là giá trị bất thường so với cả hai giá trị x và y.
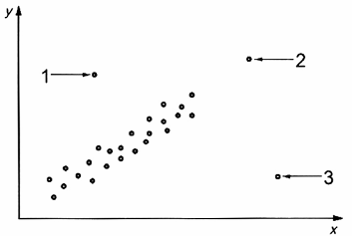
CHÚ DẪN:
1,2,3 các điểm bất thường
Hình 9 - Đồ thị phân tán (Y, X)
Hình 9 cũng cho thấy rằng không phải tất cả điểm bất thường có ảnh hưởng lớn đến đường hồi quy khớp. Điểm 1 cũng không quá ảnh hưởng bởi vì số điểm trong đồ thị phân tán có giá trị x tương tự sẽ ngăn ngừa đường hồi quy dịch chuyển quá xa theo điểm 1. Điểm 1 cũng không quá ảnh hưởng bởi vì giá trị y của nó phù hợp với đường hồi quy tuyến tính hình thành bởi phần lớn các điểm dữ liệu. Ngược lại, điểm 3 có ảnh hưởng trong việc tác động đến sự khớp của đường hồi quy, vì không chỉ giá trị x là giá trị bất thường, mà giá trị y của nó cũng không phù hợp với hồi quy tuyến tính của các điểm khác.
6.3.2. Mô hình hồi quy tuyến tính
Trong việc liên hệ biến đáp ứng Y với biến giải thích đơn X, đường hồi quy tuyến tính khớp với mẫu gồm n điểm dữ liệu (yi, xi), i = 1, 2, …, n được cho bởi
|
| (15) |
và số dư thứ i được xác định khi có sự khác biệt giữa giá trị quan trắc yi và giá trị khớp tương ứng ![]() , nghĩa là
, nghĩa là
![]() , i = 1, 2, …, n
, i = 1, 2, …, n
Phương pháp bình phương tối thiểu thông thường (OLS) ước lượng b0 và b1 nhằm cực tiểu tổng bình phương sai số dư ![]() được cho bởi
được cho bởi
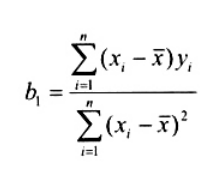
| và | (16) |
trong đó ![]() và
và ![]() tương ứng là trung bình của các quan trắc xi và yi.
tương ứng là trung bình của các quan trắc xi và yi.
Ảnh hưởng của các quan trắc bất thường X và/hoặc Y đối với việc khớp với đường hồi quy tuyến tính bằng cách sử dụng ước lượng OLS có thể được chẩn đoán bằng cách kiểm tra giá trị hồi quy OLS khớp.
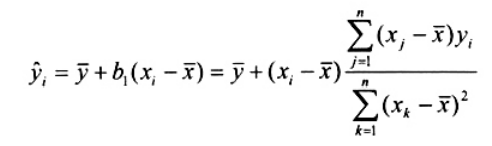
hoặc, tương đương
|
| (17) |
trong đó các giá trị
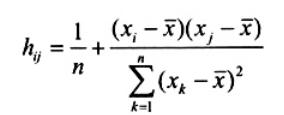
chỉ bao gồm các quan trắc về biến giải thích X. Giá trị hij hình thành một ma trận n x n đối xứng H = (hij) thường được gọi là ma trận ước lượng. Phương trình 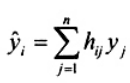 cho thấy rõ rằng giá trị hij đo lường vai trò của giá trị X trong việc xác định tầm quan trọng của giá trị quan trắc yj ảnh hưởng như thế nào đến giá trị khớp
cho thấy rõ rằng giá trị hij đo lường vai trò của giá trị X trong việc xác định tầm quan trọng của giá trị quan trắc yj ảnh hưởng như thế nào đến giá trị khớp ![]()
Tương tự, trong việc liên hệ biến đáp ứng Y với p biến giải thích X1, X2,…,Xp, hàm hồi quy khớp với mẫu n điểm dữ liệu (yi, xi1, xi2,…, xip), i = 1, 2, …, n có thể được cho bởi
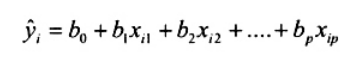
trong đó bj là hệ số hồi quy khớp thứ j và xij là giá trị cá thể thứ i của giải thích thứ j Xj. Trong trường hợp biến giải thích đơn, số dư thứ i của hàm hồi quy khớp là ![]() . Dưới dạng ma trận, mô hình hồi quy bội được viết tắt là
. Dưới dạng ma trận, mô hình hồi quy bội được viết tắt là
|
| (18) |
trong đó
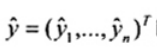 là vectơ n x 1, b = (b0, b1,…, bp)T là vectơ (p + 1) và X là ma trận n x (p + 1) có dạng
là vectơ n x 1, b = (b0, b1,…, bp)T là vectơ (p + 1) và X là ma trận n x (p + 1) có dạng
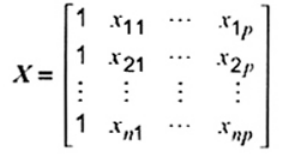
Véctơ của hệ số hồi quy bình phương nhỏ nhất được cho là
| b = (XTX)-1 XT y | (19) |
và có thể trực tiếp thu được vectơ của giá trị khớp 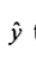 theo ma trận ước lượng H là
theo ma trận ước lượng H là
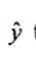 = X b = X(XTX)-1XTy = Hy
= X b = X(XTX)-1XTy = Hy
trong đó y = (y1,…, yn)T là vectơ của n giá trị quan trắc y, và
H = X(XTX)-1XT
là ma trận n x n.
6.3.3. Phát hiện quan trắc Y bất thường
Quy trình ổn định trong việc phát hiện các quan trắc Y bất thường từ mẫu cỡ n là để phân tích phần dư loại bỏ student hóa ri là các sai số dư student hóa của hàm hồi quy khớp mà không sử dụng điểm dữ liệu thứ i. Có thể tính toán phần dư loại bỏ student hóa ri như[12]
|
| (20) |
trong đó
|
| là số dư thứ i, |
| hij | là thành phần đường chéo thứ i trong ma trận ước lượng H, |
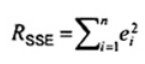 là tổng các bình phương sai số dư của hàm hồi quy khớp dựa trên n điểm dữ liệu và số lượng các thông số ước lượng trong hàm hồi quy khớp là p + 1
là tổng các bình phương sai số dư của hàm hồi quy khớp dựa trên n điểm dữ liệu và số lượng các thông số ước lượng trong hàm hồi quy khớp là p + 1
CHÚ THÍCH: Biểu thức phần dư loại bỏ student hóa ri được rút ra[12] dựa trên điểm thứ i (yi, xi1, xi2, …, xip) bị loại khi làm cho hàm hồi quy khớp với n - 1 điểm còn lại. Cũng có thể tính mà không phải khớp với hàm hồi quy mới mỗi khi một điểm dữ liệu khác biệt bị bỏ qua như có thể thấy từ phương trình (20).
Bằng cách sử dụng kết quả mà mỗi phần dư loại bỏ student hóa ri theo phân bố t với n - p - 2 bậc tự do, các điểm dữ liệu của phần dư loại bỏ student hóa có giá trị tuyệt đối lớn hơn t1-a/2n; n-p-2 cần được nhận biết là bất thường so với giá trị Y.
6.3.4. Nhận biết các quan trắc X bất thường
Có thể sử dụng các thành phần đường chéo của ma trận ước lượng H để phát hiện các quan trắc X bất thường. Một số thuộc tính hữu ích của các thành phần hij trong ma trận ước lượng của mô hình hồi quy tuyến tính với tham số chắn là:
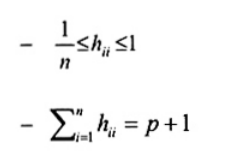
- nếu hii = 0 hoặc hii = 1 thì hij = 0 với j ¹ i
trong đó p + 1 là số lượng tham số hồi quy trong mô hình hồi quy chứa số hạng chắn.
Trong trường hợp đặc biệt của đường hồi quy tuyến tính với một biến giải thích (p = 1) và số hạng chắn các thành phần chéo hii trong ma trận ước lượng H có thể được biểu diễn như sau
|
| (21) |
Phương trình trên của hii cho thấy rằng đây là thước đo khoảng cách giữa giá trị X của điểm thứ i và trung bình giá trị X của tất cả n điểm dữ liệu. Giá trị hii lớn cho thấy rằng giá trị xi sai lệch so với phần lớn các quan trắc X và xi có thể là giá trị bất thường so với phần lớn các giá trị xj có giá trị nhỏ hơn của ![]() với j ¹ i. Thành phần chéo hii của ma trận ước lượng H trong ngữ cảnh này được gọi là đòn bẩy của quan trắc thứ i. Nhìn chung, giá trị đòn bẩy hii được coi là lớn nếu nó lớn hơn hai lần giá trị đòn bẩy trung bình
với j ¹ i. Thành phần chéo hii của ma trận ước lượng H trong ngữ cảnh này được gọi là đòn bẩy của quan trắc thứ i. Nhìn chung, giá trị đòn bẩy hii được coi là lớn nếu nó lớn hơn hai lần giá trị đòn bẩy trung bình 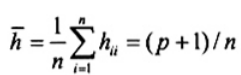 . Nguyên tắc này có nghĩa là nếu
. Nguyên tắc này có nghĩa là nếu 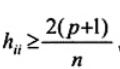 , thì giá trị quan trắc thứ i được lấy là giá trị bất thường so với giá trị x của nó. Một hướng dẫn đơn giản khác được gợi ý qua Tài liệu tham khảo [13] là
, thì giá trị quan trắc thứ i được lấy là giá trị bất thường so với giá trị x của nó. Một hướng dẫn đơn giản khác được gợi ý qua Tài liệu tham khảo [13] là
- dữ liệu với giá trị đòn bẩy nhỏ hơn 0,2 có thể an toàn đưa vào trong phân tích hồi quy,
- dữ liệu với giá trị đòn bẩy từ 0,2 đến 0,5 có thể đưa vào trong phần phân tích hồi quy,
- dữ liệu với giá trị đòn bẩy lớn hơn 0,5 cần được loại bỏ khỏi phân tích hồi quy.
6.3.5. Phát hiện các quan trắc ảnh hưởng
Sau khi nhận biết các điểm dữ liệu bất thường theo tọa độ Y và/hoặc X, bước tiếp theo là xác định xem dữ liệu bất thường này có ảnh hưởng hay không bằng cách kiểm tra xem nếu loại các điểm dữ liệu này thì có dẫn đến những thay đổi lớn trong mô hình hồi quy khớp không. Hai trong số các phép đo ảnh hưởng được sử dụng rộng rãi là giá trị DFFITS và khoảng cách Cook[12][14].
GIÁ TRỊ DFFITS
Ký hiệu DFFITS là chữ viết tắt của “độ không khớp”. Giá trị DFFITS đối với điểm dữ liệu thứ i được xác định là
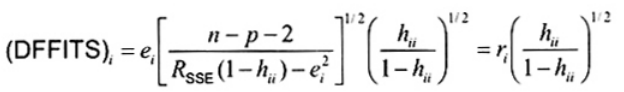 | (22) |
trong đó ri là phần dư loại bỏ student hóa trong phương trình (20). Điểm dữ liệu thứ i được công bố là điểm ảnh hưởng nếu giá trị tuyệt đối |(DFFITS)i| vượt quá 1 đối với các tập dữ liệu nhỏ hay vừa và vượt quá ![]() đối với các tập dữ liệu lớn.
đối với các tập dữ liệu lớn.
Khoảng cách Cook
Khoảng cách Cook, ký hiệu là Di được xác định như sau
|
| (23) |
trong đó ei và/hoặc hii càng lớn thì Di càng lớn. Vì vậy, giá trị Di lớn biểu thị các quan trắc ảnh hưởng. Tài liệu tham khảo [14] gợi ý là các quan trắc với khoảng cách Cook lớn hơn giá trị phân vị thứ 50 F0, 50; p+1, n-p-1 của phân bố F có thể được công bố là giá trị bất thường ảnh hưởng, trong đó n là số quan trắc, p + 1 là số tham số trong mô hình hồi quy (bao gồm cả tham số chắn) và được dùng để chỉ bậc tự do đi kèm với tử số; và n - p - 1 là bậc tự do của mẫu số. Các quan trắc có giá trị khoảng cách Cook cao hơn F0, 50; p+1, n-p-1 cần được kiểm tra về lỗi in ấn hoặc các nguyên nhân khác đối với tính cực trị của quan trắc.
CHÚ THÍCH: Các phương pháp mô tả trong điều này sẽ không hiệu quả nếu hai hoặc nhiều điểm dữ liệu bất thường ảnh hưởng gần nhau. Đã có những mở rộng cho quy trình trên để phát hiện hai hoặc nhiều điểm dữ liệu ảnh hưởng được nhóm chặt chẽ trong đó tính toán mở rộng là cần thiết.
VÍ DỤ: Dữ liệu thu được trong nghiên cứu được tiến hành để xác định mối quan hệ giữa lượng mỡ trong cơ thể (Y) với hai biến giải thích, độ dày lớp da cơ tam đầu (X1) và chu vi bắp đùi (X2), được cho trong cột 2, 3 và 4 của bảng dưới đây. Dữ liệu được lấy từ Tài liệu tham khảo [12]. Đồ thị ba chiều (Y, X1, X2) cũng được đưa ra trong Hình 10.
| Điểm dữ liệu (đối tượng) | Độ dày lớp da cơ tam đầu | Chu vi bắp đùi | Lượng mỡ cơ thể | Phần dư | Giá trị đòn bẩy | Phần dư loại bỏ student hóa |
| I | X1i | X2i | Yi | ei | hii | ri |
| 1 | 19,5 | 43,1 | 11,9 | -1,683 | 0,201 | -0,730 |
| 2 | 24,7 | 49,8 | 22,8 | 3,643 | 0,059 | 1,534 |
| 3 | 30,7 | 51,9 | 18,7 | -3,176 | 0,372 | -1,656 |
| 4 | 29,8 | 54,3 | 20,1 | -3,158 | 0,111 | -1,348 |
| 5 | 19,1 | 42,2 | 12,9 | 0,000 | 0,248 | 0,000 |
| 6 | 25,6 | 53,9 | 21,7 | -0,361 | 0,129 | -0,148 |
| 7 | 31,4 | 58,5 | 27,1 | 0,716 | 0,156 | 0,298 |
| 8 | 27,9 | 52,1 | 25,4 | 4,015 | 0,096 | 1,760 |
| 9 | 22,1 | 49,9 | 21,3 | 2,655 | 0,115 | 1,117 |
| 10 | 25,5 | 53,5 | 19,3 | -2,475 | 0,110 | -1,034 |
| 11 | 31,1 | 56,6 | 25,4 | 0,336 | 0,120 | 0,137 |
| 12 | 30,4 | 56,7 | 27,2 | 2,226 | 0,109 | 0,923 |
| 13 | 18,7 | 46,5 | 11,7 | -3,947 | 0,178 | -1,825 |
| 14 | 19,7 | 44,2 | 17,8 | 3,447 | 0,148 | 1,524 |
| 15 | 14,6 | 42,7 | 12,8 | 0,571 | 0,333 | 0,267 |
| 16 | 29,5 | 54,4 | 23,9 | 0,642 | 0,095 | 0,258 |
| 17 | 27,7 | 55,3 | 22,6 | -0,851 | 0,106 | 0,344 |
| 18 | 30,2 | 58,6 | 25,4 | -0,783 | 0,197 | 0,335 |
| 19 | 22,7 | 48,2 | 14,8 | -2,857 | 0,067 | -1,176 |
| 20 | 25,2 | 51,0 | 21,1 | 1,040 | 0,050 | 0,409 |
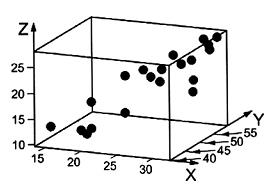
CHÚ DẪN:
X Độ dày lớp da cơ tam đầu
Y Chu vi bắp đùi
Z lượng mỡ cơ thể
Hình 10 - Đồ thị phân tán lượng mỡ cơ thể với chu vi bắp đùi với độ dày lớp da cơ tam đầu
Với phương pháp OLS hàm hồi quy khớp được cho bởi
![]()
với tổng bình phương sai số, ![]() , trong đó phần dư ei, đòn bẩy hii và phần dư loại bỏ student hóa ri của hàm hồi quy khớp được cho trong cột 5, 6 và 7, tương ứng.
, trong đó phần dư ei, đòn bẩy hii và phần dư loại bỏ student hóa ri của hàm hồi quy khớp được cho trong cột 5, 6 và 7, tương ứng.
Vì n = 20 và p = 2, khi đó bằng cách lấy mức ý nghĩa là a = 0,05, ta có
t1-a/2n;n-p-2 = t0,99875;16 = 3,5802
Vì |ri| £ 3,580 2 với tất cả i, ta kết luận rằng không có điểm dữ liệu nào có giá trị Y bất thường.
Khi phát hiện giá trị X bất thường, vì cả h33 = 0,372 và h15,15 = 0,333 vượt quá giá trị
![]()
Ta kết luận rằng các điểm 3 và 15 là bất thường đối với giá trị X của chúng.
Cuối cùng, ta phải xác định ảnh hưởng của các điểm dữ liệu 3 và 15 như thế nào trong việc làm khớp với đường hồi quy bằng cách sử dụng khoảng cách Cook tương ứng của chúng.
![]()
Và D15 = 0,212. Vì hai giá trị này đều nhỏ hơn giá trị phân vị thứ 50 F0,50; 3, 17 = 0,821 2 của phân bố F, nên cả hai điểm dữ liệu 3 và 15 đều không đủ ảnh hưởng để công bố là giá trị bất thường có ảnh hưởng.
Hàm hồi quy khớp với điểm dữ liệu 3 bị loại bỏ được cho bởi
![]()
trong đó giá trị của các tham số ước lượng là khác nhau đáng kể so với các giá trị khớp điểm dữ liệu 3.
6.3.6. Quy trình hồi quy ổn định
Một cách tiếp cận khác trong việc phát hiện giá trị bất thường trong phân tích dữ liệu hồi quy là điều chỉnh mô hình hồi quy ổn định khớp với phần lớn dữ liệu và sau đó phát hiện ra các giá trị bất thường khi các điểm đó có phần dư lớn từ phương trình ổn định. Mô hình hồi quy ổn định được sử dụng rộng rãi là hồi quy có bình phương đã cắt tỉa nhỏ nhất (LTS)[15]. Các hệ số hồi quy LTS cực tiểu hóa tổng m số dư hồi quy bình phương nhỏ nhất. Xem xét lại mẫu n dữ liệu đã cho (yi, xi1, xi2, …, xip), i = 1, 2, …, n, với giá trị làm khớp và số dư được cho tương ứng là
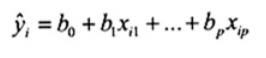
và
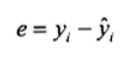
Trong trường hợp này, các hệ số hồi quy b0,b1, …, bp của hồi quy LTS là các giá trị làm cực tiểu tổng bình phương 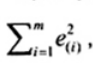 , trong đó
, trong đó ![]() là thống kê thứ tự thứ i của số dư bình phương (nghĩa là số dư được bình phương đầu tiên và sau đó xếp thứ tự), và m là số quan trắc (trong số n) được giả định là khớp thực sự với mô hình hồi quy LTS. Khi tập dữ liệu được giả định là chứa tối đa 100a % các quan trắc bất thường, cần lấy giá trị m gần với (1 - a)n nhưng không nhỏ hơn giá trị nguyên [(n + p + 1)/2]. Khi đó, các quan trắc có số dư lớn được xác định là giá trị bất thường.
là thống kê thứ tự thứ i của số dư bình phương (nghĩa là số dư được bình phương đầu tiên và sau đó xếp thứ tự), và m là số quan trắc (trong số n) được giả định là khớp thực sự với mô hình hồi quy LTS. Khi tập dữ liệu được giả định là chứa tối đa 100a % các quan trắc bất thường, cần lấy giá trị m gần với (1 - a)n nhưng không nhỏ hơn giá trị nguyên [(n + p + 1)/2]. Khi đó, các quan trắc có số dư lớn được xác định là giá trị bất thường.
CHÚ THÍCH: Ước lượng của hệ số hồi quy LTS sẵn có trong phần mềm thống kê có bản quyền.
VÍ DỤ: Dữ liệu hai biến của 6.2 được vẽ đồ thị trên Hình 11 cùng với hai đường hồi quy của biến đáp ứng x2 (y) đến x1(x), nghĩa là đường hồi quy bình phương nhỏ nhất thông thường (OLS) làm cực tiểu tổng bình phương số dư, và đường hồi quy bình phương đã cắt tỉa nhỏ nhất (LTS) làm cực tiểu tổng bình phương số dư đã cắt tỉa với m = [0,9n].
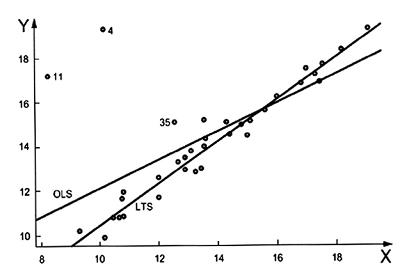
Các điểm đánh dấu 4, 11 và 35 là các điểm được coi là giá trị bất thường trong 6.2.
Hình 11 - So sánh đường hồi quy bình phương đã cắt tỉa nhỏ nhất (LTS) và đường hồi quy bình phương nhỏ nhất thông thường (OLS)
Lưu ý rằng hai điểm ảnh hưởng nhất ở góc trên cùng bên trái kéo đường OLS ra khỏi nhóm chính của tập dữ liệu đã được điều chỉnh rất khớp với đường LTS. Quy trình hồi quy LTS ổn định về cơ bản bỏ qua hai điểm ảnh hưởng này vì chỉ khoảng 90 % dữ liệu được đưa vào làm khớp đường LTS.
Phụ lục A
(tham khảo)
Thuật toán dùng cho quy trình phát hiện giá trị bất thường GESD
Giả sử là mẫu x1, x2, … xn cỡ n được lấy từ phân bố chuẩn. Thuật toán sau đây mô tả các bước cần thiết đối với việc phát hiện m giá trị bất thường có thể bằng cách sử dụng quy trình độ chệch cực trị student hóa tổng quát (GESD) ở mức ý nghĩa a.
Đọc a, m.
Đặt l = 0
Đặt I0 = {x1, x2, …, xn}
LẶP LẠI
Tính trung bình mẫu ![]() và độ lệch chuẩn mẫu s(Il) từ mẫu Il.
và độ lệch chuẩn mẫu s(Il) từ mẫu Il.
Tính toán thống kê 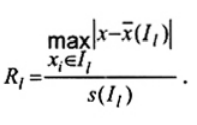
Tính phân vị thứ 100p tp; n-l-2 của phân bố t với (n - l - 2) bậc tự do, trong đó p = (1 - a/2)1/(n - l)
Tính giá trị tới hạn 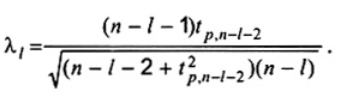
Đặt Il+1 = Il/{x(l)}. (Xem Chú thích 1)
Đặt l = l + 1
ĐẾN KHI l = m
Đặt l = 0
LẶP LẠI
Nếu (Ri > li), thì công bố x(l) (giá trị của x trong Il đưa đến giá trị Rl) là giá trị bất thường.
Đặt l = l + 1
ĐẾN KHI l = m
CHÚ THÍCH 1: Thu được Il + 1 là mẫu rút gọn cỡ n - l bằng cách xóa điểm dữ liệu x(l) trong mẫu Il đưa đến giá trị Rl.
CHÚ THÍCH 2: Nếu (Rl £ li) với tất cả l = 0, 1, 2, …, m, thì kết luận rằng không có giá trị bất thường nào trong mẫu.
PHỤ LỤC B
(quy định)
Giá trị tới hạn của thống kê kiểm nghiệm giá trị bất thường đối với mẫu hàm mũ
Bảng B.1 - Giá trị tới hạn 2,5% và 1% gE;n dưới và trên của thống kê kiểm nghiệm Greenwood GE đối với mẫu hàm mũ
| n | Dưới 1% | Dưới 2,5% | Trên 2,5% | Trên 1% | n | Dưới 1% | Dưới 2,5% | Trên 2,5% | Trên 1% | n | Dưới 1% | Dưới 2,5% | Trên 2,5% | Trên 1% |
| 2 | 0,500 0 | 0,500 3 | 0,975 4 | 0,990 1 | 34 | 0,042 8 | 0,044 3 | 0,079 0 | 0,086 3 | 82 | 0,019 5 | 0,020 1 | 0,030 1 | 0,031 9 |
| 3 | 0,336 0 | 0,340 2 | 0,831 4 | 0,890 1 | 35 | 0,041 7 | 0,043 1 | 0,076 5 | 0,083 5 | 84 | 0,019 1 | 0,019 6 | 0,029 3 | 0,031 1 |
| 4 | 0,258 5 | 0,265 8 | 0,682 8 | 0,756 3 | 36 | 0,040 7 | 0,042 1 | 0,074 2 | 0,080 9 | 86 | 0,018 7 | 0,019 2 | 0,028 6 | 0,030 2 |
| 5 | 0,213 7 | 0,221 7 | 0,568 0 | 0,640 0 | 37 | 0,039 7 | 0,041 1 | 0,072 0 | 0,078 4 | 88 | 0,018 3 | 0,018 8 | 0,027 9 | 0,029 5 |
| 6 | 0,183 8 | 0,191 4 | 0,482 1 | 0,547 4 | 38 | 0,038 8 | 0,040 1 | 0,069 9 | 0,076 1 | 90 | 0,017 9 | 0,018 4 | 0,027 2 | 0,028 8 |
| 7 | 0,162 0 | 0,168 9 | 0,417 3 | 0,474 9 | 39 | 0,037 9 | 0,039 2 | 0,068 0 | 0,073 8 | 92 | 0,017 6 | 0,018 0 | 0,026 6 | 0,028 1 |
| 8 | 0,145 2 | 0,151 4 | 0,366 7 | 0,417 3 | 40 | 0,037 1 | 0,038 3 | 0,066 1 | 0,071 7 | 94 | 0,017 3 | 0,017 7 | 0,026 0 | 0,027 4 |
| 9 | 0,131 8 | 0,137 4 | 0,326 3 | 0,371 0 | 41 | 0,036 3 | 0,037 5 | 0,064 3 | 0,069 8 | 96 | 0,016 9 | 0,017 4 | 0,025 4 | 0,026 8 |
| 10 | 0,120 8 | 0,126 0 | 0,293 4 | 0,333 1 | 42 | 0,035 5 | 0,036 7 | 0,062 6 | 0,067 9 | 98 | 0,016 6 | 0,017 0 | 0,024 8 | 0,026 2 |
| 11 | 0,111 6 | 0,116 4 | 0,266 1 | 0,301 6 | 43 | 0,034 8 | 0,035 9 | 0,061 0 | 0,066 1 | 100 | 0,016 3 | 0,016 7 | 0,024 3 | 0,025 6 |
| 12 | 0,103 9 | 0,108 2 | 0,243 1 | 0,275 1 | 44 | 0,034 1 | 0,035 2 | 0,059 5 | 0,064 4 | 105 | 0,015 6 | 0,016 0 | 0,023 0 | 0,024 2 |
| 13 | 0,097 2 | 0,101 2 | 0,223 6 | 0,252 5 | 45 | 0,033 4 | 0,034 5 | 0,058 1 | 0,062 8 | 110 | 0,014 9 | 0,015 3 | 0,021 9 | 0,023 0 |
| 14 | 0,091 3 | 0,095 1 | 0,206 8 | 0,233 0 | 46 | 0,032 8 | 0,033 8 | 0,056 7 | 0,061 2 | 115 | 0,014 3 | 0,014 7 | 0,020 9 | 0,021 9 |
| 15 | 0,086 2 | 0,089 7 | 0,192 2 | 0,216 1 | 47 | 0,032 2 | 0,033 2 | 0,055 4 | 0,059 7 | 120 | 0,013 8 | 0,014 1 | 0,019 9 | 0,020 9 |
| 16 | 0,081 6 | 0,084 9 | 0,179 4 | 0,201 3 | 48 | 0,031 6 | 0,032 6 | 0,054 1 | 0,058 3 | 125 | 0,013 3 | 0,013 6 | 0,019 1 | 0,020 0 |
| 17 | 0,077 6 | 0,080 7 | 0,168 1 | 0,188 3 | 49 | 0,031 0 | 0,032 0 | 0,052 9 | 0,057 0 | 130 | 0,012 8 | 0,013 1 | 0,118 3 | 0,019 1 |
| 18 | 0,073 9 | 0,076 8 | 0,158 1 | 0,176 3 | 50 | 0,030 5 | 0,031 4 | 0,051 7 | 0,055 7 | 135 | 0,012 4 | 0,012 7 | 0,017 6 | 0,018 4 |
| 19 | 0,070 6 | 0,073 4 | 0,149 1 | 0,166 4 | 52 | 0,029 4 | 0,030 3 | 0,049 6 | 0,053 3 | 140 | 0,012 0 | 0,012 2 | 0,016 9 | 0,017 6 |
| 20 | 0,067 6 | 0,070 2 | 0,141 1 | 0,157 2 | 54 | 0,028 4 | 0,029 3 | 0,047 5 | 0,051 1 | 145 | 0,011 6 | 0,011 8 | 0,016 3 | 0,017 0 |
| 21 | 0,064 8 | 0,067 3 | 0,133 8 | 0,148 8 | 56 | 0,027 5 | 0,028 4 | 0,045 7 | 0,049 0 | 150 | 0,011 2 | 0,011 5 | 0,015 7 | 0,016 3 |
| 22 | 0,062 3 | 0,064 7 | 0,127 2 | 0,141 2 | 58 | 0,026 7 | 0,027 5 | 0,044 0 | 0,047 1 | 155 | 0,010 9 | 0,011 1 | 0,015 2 | 0,015 8 |
| 23 | 0,060 0 | 0,062 3 | 0,121 2 | 0,134 3 | 60 | 0,025 9 | 0,026 7 | 0,042 4 | 0,045 3 | 160 | 0,010 6 | 0,010 8 | 0,014 6 | 0,015 2 |
| 24 | 0,057 8 | 0,060 0 | 0,115 7 | 0,128 0 | 62 | 0,025 1 | 0,025 9 | 0,040 9 | 0,043 7 | 165 | 0,010 3 | 0,015 5 | 0,014 2 | 0,014 7 |
| 25 | 0,055 8 | 0,057 9 | 0,110 7 | 0,122 3 | 64 | 0,024 4 | 0,025 1 | 0,039 5 | 0,042 1 | 170 | 0,010 0 | 0,010 2 | 0,013 7 | 0,014 3 |
| 26 | 0,054 0 | 0,056 0 | 0,106 0 | 0,177 0 | 66 | 0,023 8 | 0,024 4 | 0,038 2 | 0,040 7 | 175 | 0,009 7 | 0,009 9 | 0,013 3 | 0,013 8 |
| 27 | 0,052 2 | 0,054 2 | 0,101 7 | 0,112 1 | 68 | 0,023 1 | 0,023 8 | 0,036 9 | 0,039 4 | 180 | 0,009 5 | 0,009 7 | 0,012 9 | 0,013 4 |
| 28 | 0,050 6 | 0,052 5 | 0,097 8 | 0,107 6 | 70 | 0,022 5 | 0,023 2 | 0,035 8 | 0,038 1 | 185 | 0,009 2 | 0,009 4 | 0,012 5 | 0,013 0 |
| 29 | 0,049 1 | 0,050 9 | 0,094 1 | 0,103 4 | 72 | 0,022 0 | 0,022 6 | 0,034 7 | 0,036 9 | 190 | 0,009 0 | 0,009 2 | 0,012 2 | 0,012 6 |
| 30 | 0,047 7 | 0,049 4 | 0,090 6 | 0,099 5 | 74 | 0,021 4 | 0,022 0 | 0,033 7 | 0,035 8 | 195 | 0,008 8 | 0,009 0 | 0,011 9 | 0,012 3 |
| 31 | 0,046 4 | 0,048 0 | 0,087 4 | 0,095 8 | 76 | 0,020 9 | 0,021 5 | 0,032 7 | 0,034 7 | 200 | 0,008 6 | 0,008 7 | 0,011 5 | 0,012 0 |
| 32 | 0,045 1 | 0,046 7 | 0,084 4 | 0,092 4 | 78 | 0,020 4 | 0,021 0 | 0,031 8 | 0,033 7 | 225 | 0,007 7 | 0,007 8 | 0,010 2 | 0,010 5 |
| 33 | 0,043 9 | 0,045 4 | 0,081 6 | 0,089 3 | 80 | 0,020 0 | 0,020 5 | 0,030 9 | 0,032 8 | 250 | 0,007 0 | 0,007 1 | 0,009 1 | 0,009 4 |
| CHÚ THÍCH 1: Mỗi giá trị tới hạn này thu được dựa trên một trăm triệu mẫu hàm mũ mô phỏng cỡ n. CHÚ THÍCH 2: Mỗi giá trị trong bảng được làm tròn lên ở số thập phân thứ tư để đảm bảo mức ý nghĩa | ||||||||||||||
Bảng B.2 - Giá trị tới hạn trên 5% và 1% đối với kiểm nghiệm liên tiếp cho đến m = 2 giá trị bất thường trên đối với mẫu hàm mũ
| m = 2 | |||||||||
|
| 5% | 1% |
| 5% | 1% | ||||
| n |
|
|
|
| n |
|
|
|
|
| 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 32 34 36 38 40 42 44 | 0,434 8 0,401 0 0,372 4 0,348 0 0,326 8 0,308 2 0,291 6 0,277 0 0,263 7 0,251 9 0,241 3 0,231 3 0,222 4 0,214 2 0,206 5 0,199 5 0,192 9 0,186 8 0,181 2 0,175 7 0,170 8 0,161 7 0,153 5 0,146 2 0,139 7 0,133 7 0,128 3 0,123 3 | 0,483 4 0,453 3 0,426 9 0,403 3 0,382 7 0,363 9 0,347 3 0,332 0 0,318 3 0,305 8 0,294 1 0,283 4 0,273 5 0,264 4 0,255 8 0,247 8 0,240 3 0,233 3 0,226 8 0,220 7 0,214 8 0,204 1 0,194 4 0,185 7 0,177 7 0,170 6 0,163 9 0,157 8 | 0,514 3 0,474 8 0,441 2 0,412 5 0,386 8 0,364 7 0,344 7 0,327 3 0,311 4 0,297 1 0,284 5 0,272 3 0,261 8 0,251 9 0,242 6 0,234 0 0,226 3 0,219 0 0,212 3 0,205 8 0,199 8 0,189 0 0,179 2 0,170 5 0,162 7 0,155 5 0,149 1 0,143 2 | 0,569 6 0,536 3 0,506 6 0,479 3 0,455 5 0,434 5 0,414 9 0,397 2 0,381 3 0,366 7 0,352 9 0,340 3 0,328 6 0,317 5 0,307 4 0,298 0 0,288 8 0,280 5 0,272 9 0,265 4 0,258 4 0,245 7 0,233 9 0,233 5 0,213 9 0,205 1 0,197 2 0,189 8 | 46 48 50 55 60 65 70 75 80 85 90 95 100 110 120 130 140 150 160 170 180 190 200 220 240 260 280 300 | 0,118 7 0,114 5 0,110 6 0,102 0 0,094 6 0,088 4 0,083 0 0,078 3 0,074 1 0,070 3 0,067 0 0,063 9 0,061 2 0,056 4 0,052 4 0,048 9 0,045 8 0,043 2 0,040 9 0,038 8 0,036 9 0,035 3 0,033 7 0,031 2 0,028 9 0,026 9 0,025 2 0,023 8 | 0,152 2 0,147 0 0,142 1 0,131 4 0,122 2 0,114 3 0,107 4 0,101 3 0,096 0 0,091 2 0,086 9 0,083 0 0,079 4 0,073 2 0,067 9 0,063 4 0,059 5 0,056 0 0,053 0 0,050 3 0,047 8 0,045 6 0,043 6 0,040 4 0,037 3 0,034 7 0,032 5 0,030 6 | 0,137 6 0,132 7 0,128 2 0,177 9 0,109 2 0,102 0 0,095 5 0,089 9 0,084 9 0,080 7 0,076 7 0,073 2 0,070 0 0,064 4 0,059 6 0,055 6 0,052 1 0,049 1 0,046 4 0,044 0 0,041 8 0,039 9 0,038 1 0,035 1 0,032 5 0,030 3 0,028 4 0,026 7 | 0,183 0 0,176 9 0,170 8 0,157 8 0,146 7 0,137 1 0,128 7 0,121 4 0,115 0 0,109 2 0,103 9 0,099 2 0,094 9 0,087 3 0,081 0 0,075 5 0,070 8 0,066 6 0,062 9 0,059 6 0,056 7 0,054 0 0,051 6 0,047 4 0,043 9 0,040 9 0,038 2 0,035 9 |
Bảng B.3 - Giá trị tới hạn trên 5% và 1% đối với kiểm nghiệm liên tiếp cho đến m = 3 giá trị bất thường trên đối với mẫu hàm mũ
| m = 3 | |||||||||||||
|
| 5% | 1% |
| 5% | 1% | ||||||||
| n |
|
|
|
|
|
| n |
|
|
|
|
|
|
| 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 32 34 36 38 40 42 44 46 48 50 | 0,305 8 0,287 5 0,271 2 0,257 0 0,244 1 0,232 5 0,222 1 0,212 5 0,204 0 0,196 1 0,189 0 0,182 3 0,176 1 0,170 3 0,164 9 0,160 0 0,150 9 0,142 8 0,135 6 0,129 2 0,123 4 0,118 2 0,113 4 0,109 1 0,105 0 0,101 3 | 0,321 0 0,303 5 0,288 1 0,274 3 0,261 9 0,250 7 0,240 3 0,230 9 0,222 4 0,214 2 0,206 8 0,200 0 0,193 7 0,187 8 0,182 1 0,177 0 0,167 4 0,158 9 0,151 3 0,144 4 0,138 2 0,132 6 0,127 4 0,122 6 0,118 2 0,114 2 | 0,380 3 0,363 0 0,347 0 0,332 6 0,319 5 0,307 2 0,296 2 0,285 7 0,276 1 0,267 2 0,258 7 0,250 9 0,243 6 0,236 8 0,230 3 0,224 1 0,212 9 0,202 8 0,193 6 0,185 3 0,177 8 0,170 8 0,164 4 0,158 5 0,153 1 0,148 0 | 0,357 7 0,336 0 0,316 5 0,299 4 0,283 7 0,269 8 0,257 9 0,246 2 0,236 2 0,226 8 0,218 1 0,210 4 0,202 9 0,196 2 0,189 7 0,184 0 0,173 0 0,163 7 0,155 2 0,147 6 0,140 9 0,134 8 0,129 1 0,124 0 0,119 3 0,115 0 | 0,377 5 0,356 9 0,338 7 0,322 2 0,307 4 0,294 5 0,281 7 0,270 7 0,260 5 0,250 7 0,241 9 0,233 8 0,226 3 0,219 1 0,212 5 0,206 3 0,195 1 0,184 9 0,175 8 0,167 9 0,160 3 0,153 7 0,147 4 0,141 8 0,136 7 0,132 0 | 0,449 7 0,429 6 0,411 2 0,394 9 0,379 8 0,356 8 0,352 5 0,340 4 0,329 0 0,318 6 0,308 7 0,299 3 0,290 7 0,282 9 0,274 9 0,268 0 0,254 6 0,242 6 0,231 8 0,221 8 0,212 5 0,204 4 0,196 9 0,189 8 0,183 4 0,176 9 | 55 60 65 70 75 80 85 90 95 100 110 120 130 140 150 160 170 180 190 200 220 240 260 280 300 | 0,093 1 0,086 3 0,080 4 0,075 4 0,071 0 0,067 1 0,063 7 0,060 6 0,057 8 0,055 3 0,050 9 0,047 2 0,044 1 0,041 3 0,039 0 0,036 8 0,035 0 0,033 3 0,031 8 0,030 4 0,028 0 0,026 0 0,024 2 0,022 7 0,021 4 | 0,105 2 0,097 6 0,091 2 0,085 5 0,080 6 0,076 2 0,072 4 0,068 9 0,065 8 0,062 9 0,058 0 0,053 8 0,050 2 0,047 1 0,044 4 0,042 0 0,039 8 0,037 9 0,036 2 0,034 6 0,031 8 0,029 5 0,027 6 0,025 8 0,024 3 | 0,136 7 0,127 1 0,118 9 0,111 7 0,105 4 0,099 7 0,094 7 0,090 2 0,086 2 0,082 4 0,076 0 0,070 5 0,065 8 0,061 6 0,058 1 0,054 9 0,052 1 0,049 5 0,047 2 0,045 2 0,041 5 0,038 5 0,035 9 0,033 6 0,031 6 | 0,105 6 0,097 5 0,090 8 0,084 9 0,079 9 0,075 4 0,071 5 0,067 9 0,064 8 0,061 9 0,056 9 0,052 7 0,049 1 0,046 0 0,043 3 0,040 9 0,038 8 0,036 9 0,035 2 0,033 6 0,030 9 0,028 7 0,026 7 0,025 0 0,023 6 | 0,121 4 0,112 4 0,104 8 0,098 1 0,092 4 0,087 2 0,082 9 0,078 7 0,075 2 0,071 8 0,066 0 0,061 2 0,057 0 0,053 5 0,050 3 0,047 5 0,045 1 0,042 8 0,040 9 0,039 0 0,035 9 0,033 2 0,031 0 0,029 0 0,027 3 | 0,163 5 0,152 0 0,142 1 0,133 3 0,125 7 0,119 0 0,113 0 0,107 6 0,102 6 0,098 1 0,090 3 0,083 7 0,078 0 0,073 1 0,068 8 0,065 0 0,061 6 0,058 5 0,055 7 0,053 3 0,048 9 0,045 3 0,042 1 0,039 4 0,037 0 |
Bảng B.4 - Giá trị tới hạn trên 5 % và 1 % đối với kiểm nghiệm liên tiếp cho đến m = 4 giá trị bất thường trên đối với mẫu hàm mũ
| m = 4 | ||||||||
|
| 5% | 1% | ||||||
| n |
|
|
|
|
|
|
|
|
| 20 21 22 23 24 25 26 27 28 29 30 32 34 36 38 40 42 44 46 48 50 55 60 65 70 75 80 85 90 95 100 110 120 130 140 150 160 170 180 190 200 220 240 260 280 300 | 0,231 9 0,220 8 0,210 4 0,201 3 0,192 8 0,185 2 0,178 1 0,171 6 0,165 6 0,160 2 0,154 9 0,145 6 0,137 5 0,130 2 0,123 8 0,118 0 0,112 8 0,108 0 0,103 7 0,099 7 0,096 0 0,088 1 0,081 4 0,075 8 0,070 9 0,066 7 0,063 0 0,059 7 0,056 8 0,054 1 0,051 7 0,047 6 0,044 1 0,041 1 0,038 6 0,036 3 0,034 3 0,032 6 0,031 0 0,029 6 0,028 3 0,026 1 0,024 2 0,022 6 0,021 2 0,020 0 | 0,238 1 0,227 4 0,217 5 0,208 8 0,200 7 0,193 2 0,186 3 0,180 0 0,174 0 0,168 5 0,163 4 0,154 1 0,145 8 0,138 4 0,131 8 0,125 9 0,120 5 0,115 6 0,111 1 0,107 0 0,103 2 0,094 8 0,087 8 0,081 8 0,076 7 0,072 2 0,068 2 0,064 7 0,061 6 0,058 7 0,056 2 0,051 7 0,047 9 0,044 7 0,042 0 0,039 5 0,037 4 0,035 5 0,033 7 0,032 2 0,030 8 0,028 4 0,026 3 0,024 6 0,023 0 0,021 7 | 0,257 3 0,246 5 0,236 9 0,228 0 0,219 6 0,212 0 0,204 9 0,198 4 0,192 4 0,186 6 0,181 1 0,171 3 0,162 6 0,154 7 0,147 7 0,141 3 0,135 5 0,130 2 0,125 2 0,120 8 0,116 6 0,107 4 0,099 6 0,093 0 0,087 2 0,082 2 0,077 7 0,073 8 0,070 2 0,067 0 0,064 1 0,059 0 0,054 7 0,051 1 0,047 9 0,045 1 0,042 7 0,040 5 0,038 5 0,036 8 0,035 2 0,032 4 0,030 0 0,028 0 0,026 2 0,024 7 | 0,316 4 0,304 9 0,294 1 0,284 2 0,275 0 0,266 2 0,258 1 0,250 7 0,243 6 0,236 9 0,230 5 0,219 0 0,208 5 0,199 0 0,190 5 0,182 7 0,175 5 0,168 9 0,162 8 0,157 2 0,151 9 0,140 4 0,130 5 0,122 0 0,114 6 0,108 0 0,102 3 0,097 2 0,092 5 0,088 3 0,084 5 0,077 8 0,072 2 0,067 3 0,063 1 0,059 5 0,056 2 0,053 3 0,050 7 0,048 3 0,046 2 0,042 5 0,039 3 0,036 6 0,034 3 0,032 3 | 0,267 5 0,254 4 0,242 0 0,231 0 0,221 1 0,212 1 0,203 7 0,196 1 0,189 0 0,182 5 0,176 4 0,165 4 0,155 9 0,147 3 0,140 0 0,133 0 0,127 1 0,121 5 0,116 6 0,112 0 0,107 7 0,098 6 0,090 9 0,084 5 0,078 9 0,074 1 0,069 9 0,066 2 0,062 9 0,059 8 0,057 2 0,052 5 0,048 6 0,045 2 0,042 4 0,039 8 0,037 6 0,035 7 0,033 9 0,032 3 0,030 9 0,028 4 0,026 4 0,024 6 0,023 0 0,021 7 | 0,275 8 0,263 5 0,251 5 0,241 2 0,231 6 0,222 7 0,214 8 0,207 2 0,200 2 0,193 4 0,187 6 0,176 3 0,166 8 0,158 1 0,150 4 0,143 5 0,137 2 0,131 4 0,126 2 0,121 4 0,117 0 0,107 3 0,099 2 0,092 3 0,086 3 0,081 1 0,076 5 0,072 6 0,068 9 0,065 7 0,062 8 0,057 7 0,053 4 0,049 8 0,046 6 0,043 9 0,041 4 0,039 3 0,037 4 0,035 6 0,034 0 0,031 3 0,029 0 0,027 0 0,025 3 0,023 9 | 0,301 3 0,288 3 0,277 0 0,266 2 0,256 3 0,247 3 0,239 0 0,231 3 0,223 8 0,217 1 0,210 9 0,199 3 0,188 9 0,179 5 0,171 4 0,163 6 0,156 7 0,150 4 0,144 6 0,139 3 0,134 5 0,123 7 0,114 5 0,106 8 0,099 9 0,094 1 0,088 8 0,084 3 0,080 1 0,076 5 0,073 0 0,067 2 0,062 2 0,057 9 0,054 3 0,051 1 0,048 3 0,045 8 0,043 5 0,041 5 0,039 6 0,036 4 0,033 7 0,031 4 0,029 4 0,027 7 | 0,374 7 0,360 7 0,348 5 0,336 8 0,326 3 0,316 3 0,306 5 0,297 6 0,289 7 0,281 7 0,274 5 0,260 7 0,248 3 0,237 3 0,227 0 0,217 7 0,209 2 0,201 5 0,194 3 0,187 8 0,181 1 0,167 2 0,155 5 0,145 4 0,136 3 0,128 6 0,121 7 0,115 5 0,109 9 0,105 0 0,100 3 0,092 3 0,085 5 0,079 7 0,074 6 0,070 2 0,066 4 0,062 9 0,059 7 0,056 9 0,054 3 0,049 9 0,046 2 0,043 0 0,040 2 0,037 8 |
Bảng B.5 - Giá trị tới hạn trên 5% và 1% đối với kiểm nghiệm liên tiếp cho đến m = 2 giá trị bất thường dưới đối với mẫu hàm mũ
| m = 2 | |||||||||
|
| 5% | 1% |
| 5% | 1% | ||||
| n |
|
|
|
| n |
|
|
|
|
| 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | 0,836 7 0,834 4 0,832 6 0,831 4 0,830 3 0,829 2 0,828 3 0,827 0 0,826 6 0,826 1 0,825 4 0,824 8 0,824 5 0,824 1 0,823 6 0,823 6 0,823 1 0,822 8 0,822 5 | 0,977 5 0,977 3 0,977 0 0,976 9 0,976 7 0,976 6 0,976 5 0,976 4 0,976 4 0,976 3 0,976 3 0,976 2 0,976 2 0,976 1 0,976 1 0,976 0 0,976 0 0,975 9 0,976 0 | 0,921 6 0,920 0 0,919 1 0,917 7 0,917 4 0,917 3 0,916 3 0,915 7 0,915 7 0,915 1 0,914 6 0,914 5 0,914 1 0,914 0 0,914 0 0,913 7 0,913 5 0,913 2 0,913 0 | 0,995 5 0,995 5 0,995 5 0,995 4 0,995 4 0,995 3 0,995 3 0,995 3 0,995 3 0,995 3 0,995 3 0,995 2 0,995 2 0,995 2 0,995 2 0,995 2 0,995 2 0,995 2 0,995 2 | 29 30 35 40 45 50 60 70 80 90 100 120 140 160 180 200 300 | 0,822 4 0,822 4 0,821 2 0,820 4 0,819 8 0,819 1 0,818 9 0,817 9 0,817 9 0,817 2 0,817 2 0,816 6 0,816 6 0,816 6 0,816 2 0,815 9 0,815 7 | 0,975 9 0,975 8 0,975 7 0,975 6 0,975 5 0,975 5 0,975 5 0,975 4 0,975 3 0,975 3 0,975 2 0,975 2 0,975 2 0,975 1 0,975 1 0,975 1 0,975 1 | 0,913 0 0,912 8 0,912 2 0,911 7 0,911 4 0,911 1 0,910 8 0,910 2 0,909 9 0,909 9 0,910 0 0,909 5 0,909 1 0,909 1 0,908 9 0,908 9 0,909 2 | 0,995 2 0,995 2 0,995 2 0,995 2 0,995 1 0,995 1 0,995 1 0,995 1 0,995 1 0,995 1 0,995 1 0,995 0 0,995 0 0,995 0 0,995 0 0,995 0 0,995 0 |
Bảng B.6 - Giá trị tới hạn trên 5% và 1% đối với kiểm nghiệm liên tiếp cho đến m = 3 giá trị bất thường dưới đối với mẫu hàm mũ
| m = 3 | |||||||||||||
|
| 5% | 1% |
| 5% | 1% | ||||||||
| n |
|
|
|
|
|
| n |
|
|
|
|
|
|
| 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | 0,705 1 0,703 5 0,701 9 0,700 7 0,699 0 0,698 0 0,697 0 0,696 4 0,695 6 0,694 8 0,693 9 0,693 5 0,692 9 0,692 4 0,691 9 0,691 5 | 0,855 5 0,854 4 0,853 6 0,853 2 0,852 7 0,852 0 0,851 7 0,851 1 0,850 7 0,850 2 0,850 3 0,849 9 0,849 5 0,849 3 0,849 1 0,849 1 | 0,984 0 0,984 0 0,983 9 0,983 9 0,983 8 0,983 8 0,983 7 0,983 7 0,983 7 0,983 6 0,983 6 0,983 6 0,983 5 0,983 5 0,983 5 0,983 4 | 0,807 3 0,806 2 0,805 0 0,803 4 0,802 7 0,801 5 0,801 1 0,799 5 0,799 5 0,798 8 0,797 8 0,798 0 0,797 0 0,797 2 0,796 9 0,796 5 | 0,931 4 0,930 6 0,930 0 0,930 0 0,929 6 0,929 0 0,928 8 0,928 6 0,928 5 0,928 5 0,928 1 0,928 3 0,928 0 0,927 9 0,927 8 0,927 6 | 0,996 9 0,996 9 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 0,996 8 | 40 50 60 70 80 90 100 120 140 160 180 200 250 300 | 0,688 8 0,687 1 0,685 2 0,684 3 0,683 8 0,683 0 0,683 2 0,682 7 0,682 1 0,682 1 0,681 7 0,681 3 0,681 2 0,680 4 | 0,847 2 0,846 2 0,845 9 0,844 9 0,844 9 0,844 3 0,844 4 0,843 8 0,843 4 0,843 7 0,843 6 0,843 7 0,843 2 0,843 1 | 0,983 3 0,983 2 0,983 2 0,983 2 0,983 1 0,983 1 0,983 0 0,983 0 0,983 0 0,983 0 0,982 9 0,983 0 0,982 9 0,982 9 | 0,793 7 0,792 2 0,791 1 0,790 4 0,789 5 0,789 5 0,788 7 0,788 5 0,788 2 0,788 7 0,787 4 0,786 6 0,786 9 0,786 3 | 0,926 6 0,926 0 0,925 7 0,925 3 0,925 1 0,925 0 0,925 3 0,924 7 0,924 4 0,924 5 0,924 2 0,924 2 0,923 9 0,924 3 | 0,996 8 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 7 0,996 6 |
Bảng B.7 - Giá trị tới hạn trên 5 % và 1 % đối với kiểm nghiệm liên tiếp cho đến m = 4 giá trị bất thường dưới đối với mẫu hàm mũ
| m = 4 | ||||||||
|
| 5% | 1% | ||||||
| n |
|
|
|
|
|
|
|
|
| 20 21 22 23 24 25 26 28 30 35 40 45 50 70 100 150 200 | 0,596 1 0,594 6 0,593 1 0,592 0 0,591 6 0,590 3 0,589 1 0,587 8 0,586 7 0,584 2 0,582 3 0,580 8 0,597 7 0,577 4 0,574 9 0,573 3 0,572 8 | 0,717 0 0,716 3 0,715 2 0,714 5 0,713 8 0,713 0 0,712 5 0,711 6 0,710 6 0,709 3 0,707 8 0,706 3 0,706 1 0,703 3 0,702 1 0,701 2 0,700 3 | 0,868 3 0,868 2 0,867 3 0,867 0 0,866 6 0,866 6 0,866 4 0,865 8 0,865 5 0,864 6 0,863 6 0,863 1 0,862 6 0,861 7 0,861 1 0,860 0 0,860 5 | 0,987 6 0,987 5 0,987 5 0,987 5 0,987 5 0,987 5 0,987 4 0,987 4 0,987 3 0,987 3 0,987 1 0,987 1 0,987 1 0,987 1 0,986 9 0,987 0 0,986 9 | 0,693 5 0,691 6 0,691 1 0,689 6 0,688 9 0,687 3 0,685 9 0,684 9 0,683 7 0,682 2 0,680 1 0,678 4 0,677 8 0,674 6 0,672 8 0,671 6 0,670 6 | 0,816 4 0,815 7 0,814 4 0,814 2 0,813 8 0,812 6 0,812 8 0,814 4 0,811 3 0,809 6 0,808 9 0,807 9 0,807 5 0,805 3 0,804 4 0,803 2 0,801 7 | 0,937 7 0,937 7 0,937 4 0,937 3 0,937 2 0,937 0 0,937 1 0,936 6 0,936 6 0,936 0 0,935 7 0,935 4 0,935 3 0,934 6 0,934 4 0,933 5 0,933 4 | 0,997 6 0,997 6 0,997 6 0,997 6 0,997 6 0,997 6 0,997 6 0,997 6 0,997 6 0,997 6 0,997 5 0,997 5 0,997 5 0,997 5 0,997 5 0,997 5 0,997 5 |
Phụ lục C
(quy định)
Giá trị hệ số của đồ thị hộp sửa đổi
Khi tham số vị trí q và tham số thang đo s của phân bố thang đo-vị trí giả thuyết Fq, s(x) là chưa biết, ước lượng tứ phân vị thứ nhất và thứ ba được ước lượng bằng phần tư dưới XL:n, và phần tư trên XU:n của mẫu n quan trắc lấy từ Fq, s(x). Có nhiều định nghĩa về độ sâu của các phần tư mẫu. Độ sâu khuyến nghị là
độ sâu phần tư ![]()
Trong đó i là phần nguyên và f là phần phân số của n/4. Hai giá trị dữ liệu với độ sâu này, cụ thể là phần tư mẫu dưới (xL:n) và phần tư mẫu trên (xU:n) trong mẫu cỡ n nhất định được đánh giá như trong 4.4.
Biểu thức chính xác thường có thể sử dụng để đánh giá các hệ số kL và kU của đồ thị hộp đối với mẫu lấy từ phân bố Fq, s(x) giả thuyết được cho trong Tài liệu tham khảo [16] là
|
| (C1) |
trong đó
a) a là tỷ lệ ngoại vi nhất định được qui định trên mẫu, nghĩa là xác suất một hoặc nhiều giá trị bất thường trong mẫu không có giá trị bất thường sẽ bị ghi sai là giá trị bất thường;
b) yl = zl:n - kL(zu:n - zl:n) và yu = zu:n - kU(zu:n - zl:n);
c) ![]() là hàm mật độ xác suất chung của zl:n và zu:n có dạng
là hàm mật độ xác suất chung của zl:n và zu:n có dạng
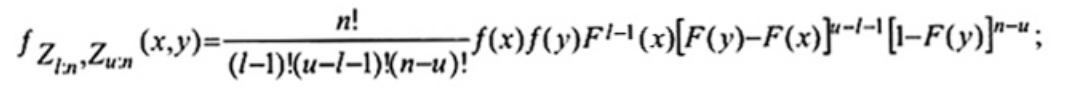
d) Zr:n = (Xr:n - q)/s là thống kê thứ tự thứ r của biến chuẩn hóa Z = (X - q)/s với hàm phân bố F(x);
e) Gl(y) = F(y)/F(zl:n) và Gu(y) = [F(y) - F(zu:n)] / [1 - F(zu:n)];
f) ![]() là hàm bêta không đầy đủ.
là hàm bêta không đầy đủ.
Có thể sử dụng thuật toán tìm trực tiếp để tìm các giá trị kL và kU thỏa mãn phương trình tích phân kép (C.1).
Đối với phân bố đối xứng, ta lấy kl = ku = (k) trong phương trình (C.1). Đối với phân bố bất đối xứng, có thể thu được giá trị kl và ku riêng rẽ bằng cách lấy P(X < LF) = 1 - Pr(X > UF), nghĩa là ![]() trong phương trình (C.1).
trong phương trình (C.1).
Giá trị kL = kU (= k) đối với mẫu cỡ 9 £ n £ 500 lấy từ phân bố chuẩn có thể được tính gần đúng từ hàm số dưới đây
| k = exp{b0 + b1ln(n) + b2ln2(n) + b3ln3(n) + b4ln4(n) + b5ln5(n)} | (C.2) |
với hệ số b5 = 0 và bi, i = 0, 1, 2, 3, 4 cho trong bảng C.1.
Cũng có thể thu được giá trị của kL và kU đối với mẫu lấy từ phân bố hàm mũ không đối xứng và phân bố cực trị từ phương trình (C.2) với hệ số bi, i = 0,1, 2, 3, 4, 5 cho trong Bảng C.2.
Đối với trường hợp khi cỡ mẫu lớn, có thể tính gần đúng giá trị của kL và kU là
![]() và
và ![]()
trong đó có thể giải thích an = 1(1 - a)1/n là tỷ lệ sai số mà một quan trắc từ mẫu ngẫu nhiên của n quan trắc bất thường được ghi sai là giá trị bất thường.
VÍ DỤ: Để phát hiện các giá trị bất thường từ mẫu chuẩn cỡ n = 20, giá trị của kL = kU (= k) đối với một tỷ lệ ngoại vi nhất định a = 0,05 được đánh giá là
k = exp {0,837 07 + 0,075 96 x ln(20) - 0,061 19 x ln2(20) + 0,013 28 x ln3(20) - 0,000 83 x ln4(20)} = exp(0,805 67) » 2,238 2
VÍ DỤ 2: Để phát hiện các giá trị bất thường từ mẫu hàm mũ cỡ n = 22, giá trị của kL và kU đối với một tỷ lệ ngoại vi nhất định a = 0,05 được đánh giá là
kL = exp {2,206 04 - 1,417 52 x ln(20) + 0,241 70 x ln2(20) - 0,020 57 x ln3(20) + 0,000 72 x ln4(20)} = exp(-408 02) » 0,665 0
kU = exp {2,741 79 - 0,770 67 x ln(22) + 0,226 88 x ln2(22) - 0,028 53 x ln3(22) + 0,001 70 x ln4(22) - 0,000 04 x ln5(22)} = exp (1,829 58) » 6,2313
Bảng C.1 - Hệ số của hàm khớp đối với các hệ số k của đồ thị hộp cỡ mẫu 9 £ n £ 500 lấy từ phân bố chuẩn với tham số chưa biết
| Phân bố chuẩn n | ||||||||
| a | mod(n,4) | b0 | b1 | b2 | b3 | b4 | b5 | d |
| 0,05 | 1 2 3 0 | 4,017 61 2,064 29 0,480 06 0,837 07 | -2,353 63 -0,885 23 0,258 54 0,075 96 | 0,646 18 0,222 37 -0,096 22 -0,061 19 | -0,078 93 -0,023 91 0,016 20 0,013 28 | 0,003 68 0,000 99 -0,000 92 -0,000 83 | - - - - | 0,014 57 0,000 64 0,004 07 0,004 62 |
| 0,01 | 1 2 3 0 | 6,379 02 3,987 72 2,148 95 2,285 07 | -3,847 70 -2,006 30 -0,652 78 -0,660 52 | 1,044 38 0,502 77 0,119 85 0,102 64 | -0,128 13 -0,056 77 -0,007 96 -0,003 93 | 0,006 01 0,002 48 0,000 13 -0,000 13 | - - - - | 0,041 83 0,006 34 0,004 17 0,006 86 |
Bảng C.2 - Hệ số của hàm khớp đối với các hệ số k của đồ thị hộp cỡ mẫu 9 £ n £ 500 lấy từ phân bố hàm mũ với tham số chưa biết
| Phân bố hàm mũ | |||||||||
| a | Yếu tố | mod(n, 4) | b0 | b1 | b2 | b3 | b4 | b5 | d |
| 0,10 | kL | 1 2 3 0 | 3,990 24 1,130 59 -1,549 86 -1,950 58 | -3,240 52 -0,721 69 1,602 82 2,261 33 | 0,955 34 0,023 06 -0,825 26 -1,147 44 | -0,159 95 0,018 04 0,178 01 0,249 30 | 0,014 40 -0,002 90 -0,018 29 -0,025 81 | -0,000 54 0,000 14 0,000 74 0,001 05 | 0,000 22 0,000 19 0,000 47 0,000 67 |
| kU | 1 2 3 0 | 3,585 01 1,797 40 0,332 62 1,086 40 | -1,567 11 -0,223 67 0,834 29 0,331 92 | 0,464 64 0,076 84 -0,217 97 -0,086 35 | -0,057 69 -0,007 33 0,029 79 0,013 96 | 0,002 71 0,000 24 -0,001 53 -0,000 80 | - - - - | 0,021 72 0,003 45 0,011 54 0,008 07 | |
| 0,05 | kL | 1 2 3 0 | 5,182 20 2,206 04 -0,575 42 -1,190 27 | -4,055 28 -1,417 52 1,020 24 1,864 02 | 1,222 29 0,241 70 -0,656 89 -1,044 28 | -0,208 33 -0,020 57 0,150 43 0,233 27 | 0,019 01 0,000 72 - 0,015 86 - 0,024 40 | -0,000 72 - 0,000 65 0,000 99 | 0,000 33 0,000 11 0,000 48 0,000 88 |
| kU | 1 2 3 0 | 5,180 29 2,741 79 0,530 26 1,310 43 | -2,967 81 -0,770 67 1,198 59 0,601 92 | 1,047 43 0,226 88 -0,502 10 -0,303 96 | -0,185 11 -0,028 53 0,109 67 0,074 56 | 0,016 83 0,001 70 -0,011 58 -0,008 32 | -0,000 63 -0,000 04 0,000 48 0,000 35 | 0,003 85 0,001 31 0,005 44 0,004 37 | |
| 0,02 | kL | 1 2 3 0 | 6,729 83 3,536 62 0,568 97 -0,381 25 | -5,174 48 -2,310 42 0,329 76 1,485 50 | 1,605 18 0,530 46 -0,455 63 -0,962 54 | -0,279 80 -0,072 55 0,117 23 0,223 51 | -0,025 96 0,005 66 -0,012 92 -0,023 80 | -0,000 99 -0,000 19 0,000 54 0,000 98 | 0,000 52 0,000 06 0,000 49 0,000 29 |
| kU | 1 2 3 0 | 5,904 97 3,794 84 2,171 27 2,677 62 | -2,952 27 -1,328 56 -0,135 25 -0,439 84 | 0,831 53 0,353 93 0,016 52 0,088 73 | -0,103 10 -0,040 15 0,002 86 -0,005 07 | 0,004 86 0,001 74 -0,000 33 0,000 01 | - - - - | 0,069 00 0,007 15 0,012 78 0,013 25 | |
CHÚ THÍCH: d là độ lệch tuyệt đối lớn nhất giữa giá trị ban đầu và giá trị khớp của k đối với mỗi lớp mod (n, 4) với 9 £ n £ 500.
Phụ lục D
(quy định)
Giá trị hệ số hiệu chỉnh đối với ước lượng ổn định của tham số đo
Bảng D.1 - Hệ số hiệu chỉnh sn và sbi của hàm ước lượng thang đo ổn định Sn và Sbi tương ứng
| Cỡ mẫu, | Hệ số | Cỡ mẫu, | Hệ số | ||
| n | sn | sbi | n | sn | sbi |
| 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | 0,886 6 2,205 1 1,138 5 1,608 1 1,185 8 1,429 7 1,198 9 1,350 0 1,201 5 1,307 4 1,200 6 1,281 4 1,199 4 1,264 7 1,197 8 1,252 6 | 1,191 2 1,382 1 1,127 2 1,185 5 1,065 0 1,111 1 1,036 9 1,076 2 1,021 9 1,056 7 1,013 6 1,044 4 1,008 6 1,036 0 1,005 0 1,029 9 | 18 19 20 30 40 50 60 70 80 90 100 120 150 200 300 500 | 1,196 1 1,243 8 1,195 1 1,192 7 1,192 1 1,192 0 1,192 0 1,192 1 1,192 1 1,192 2 1,192 3 1,192 4 1,192 5 1,192 6 1,192 7 1,192 7 | 1,002 5 1,025 2 1,000 6 0,996 2 0,994 4 0,993 5 0,992 9 0,992 5 0,992 3 0,992 1 0,992 0 0,991 8 0,991 5 0,991 4 0,991 2 0,991 0 |
Phụ lục E
(tham khảo)
Giá trị tới hạn của thống kê kiểm nghiệm Cochran
Bảng E.1 - Giá trị tới hạn 5 % của thống kê kiểm nghiệm Cochran
| p | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | n = 10 |
| 2 | 0,998 5 | 0,975 1 | 0,939 2 | 0,905 8 | 0,877 3 | 0,853 4 | 0,833 2 | 0,816 0 | 0,801 1 |
| 3 | 0,967 0 | 0,871 0 | 0,979 8 | 0,745 7 | 0,707 0 | 0,677 1 | 0,653 1 | 0,633 4 | 0,616 8 |
| 4 | 0,906 5 | 0,768 0 | 0,683 9 | 0,628 8 | 0,589 5 | 0,559 9 | 0,536 5 | 0,517 6 | 0,501 8 |
| 5 | 0,841 3 | 0,683 8 | 0,598 1 | 0,544 1 | 0,506 4 | 0,478 3 | 0,456 4 | 0,438 8 | 0,424 2 |
| 6 | 0,780 8 | 0,616 2 | 0,532 2 | 0,480 4 | 0,444 8 | 0,418 5 | 0,398 1 | 0,381 7 | 0,368 2 |
| 7 | 0,727 0 | 0,561 2 | 0,480 0 | 0,430 8 | 0,397 2 | 0,372 6 | 0,353 6 | 0,338 4 | 0,325 9 |
| 8 | 0,679 9 | 0,515 7 | 0,437 8 | 0,391 0 | 0,359 4 | 0,336 3 | 0,318 5 | 0,304 3 | 0,292 7 |
| 9 | 0,638 5 | 0,477 5 | 0,402 8 | 0,358 4 | 0,328 5 | 0,306 8 | 0,290 1 | 0,276 8 | 0,266 0 |
| 10 | 0,602 1 | 0,445 0 | 0,373 4 | 0,331 1 | 0,302 8 | 0,282 3 | 0,266 6 | 0,254 1 | 0,243 9 |
| 11 | 0,569 8 | 0,416 9 | 0,348 2 | 0,308 0 | 0,281 1 | 0,261 6 | 0,246 8 | 0,235 0 | 0,225 4 |
| 12 | 0,541 0 | 0,392 4 | 0,326 5 | 0,288 0 | 0,262 4 | 0,244 0 | 0,229 9 | 0,218 7 | 0,209 6 |
| 13 | 0,515 2 | 0,370 9 | 0,307 5 | 0,270 7 | 0,246 2 | 0,228 6 | 0,215 2 | 0,204 6 | 0,196 0 |
| 14 | 0,492 0 | 0,351 8 | 0,290 7 | 0,255 4 | 0,232 0 | 0,215 2 | 0,202 4 | 0,192 3 | 0,184 1 |
| 15 | 0,470 9 | 0,334 7 | 0,257 8 | 0,241 9 | 0,219 5 | 0,203 4 | 0,191 2 | 0,181 5 | 0,173 7 |
| 16 | 0,451 7 | 0,319 3 | 0,262 4 | 0,229 8 | 0,208 3 | 0,192 9 | 0,181 1 | 0,171 9 | 0,164 4 |
| 17 | 0,434 2 | 0,305 3 | 0,250 4 | 0,219 0 | 0,198 3 | 0,183 4 | 0,172 2 | 0,163 3 | 0,156 1 |
| 18 | 0,418 1 | 0,292 7 | 0,239 5 | 0,209 2 | 0,189 2 | 0,174 9 | 0,164 1 | 0,155 6 | 0,148 6 |
| 19 | 0,403 2 | 0,281 1 | 0,229 6 | 0,200 2 | 0,181 0 | 0,167 2 | 0,156 8 | 0,148 6 | 0,141 9 |
| 20 | 0,389 5 | 0,270 5 | 0,220 5 | 0,192 1 | 0,173 5 | 0,160 2 | 0,150 1 | 0,142 2 | 0,135 8 |
| 21 | 0,376 7 | 0,260 7 | 0,212 1 | 0,184 6 | 0,166 6 | 0,153 8 | 0,144 0 | 0,136 4 | 0,130 2 |
| 22 | 0,364 9 | 0,251 6 | 0,204 4 | 0,177 8 | 0,160 3 | 0,147 9 | 0,138 4 | 0,131 0 | 0,125 0 |
| 23 | 0,353 8 | 0,243 2 | 0,197 3 | 0,171 4 | 0,154 5 | 0,142 4 | 0,133 3 | 0,126 1 | 0,120 3 |
| 24 | 0,343 4 | 0,235 4 | 0,190 7 | 0,165 5 | 0,149 1 | 0,137 4 | 0,128 5 | 0,121 6 | 0,116 0 |
| 25 | 0,333 7 | 0,228 1 | 0,184 6 | 0,160 1 | 0,144 1 | 0,132 7 | 0,124 1 | 0,117 4 | 0,111 9 |
| 26 | 0,324 6 | 0,221 3 | 0,178 8 | 0,155 0 | 0,139 4 | 0,128 4 | 0,120 0 | 0,113 5 | 0,108 2 |
| 27 | 0,316 0 | 0,214 9 | 0,173 5 | 0,150 2 | 0,135 1 | 0,124 3 | 0,116 2 | 0,109 8 | 0,104 7 |
| 28 | 0,307 9 | 0,208 9 | 0,168 4 | 0,145 8 | 0,131 0 | 0,120 5 | 0,112 6 | 0,106 4 | 0,101 4 |
| 29 | 0,300 2 | 0,203 2 | 0,163 7 | 0,141 6 | 0,127 2 | 0,116 9 | 0,109 2 | 0,103 2 | 0,098 3 |
| 30 | 0,292 9 | 0,197 9 | 0,159 2 | 0,137 6 | 0,123 6 | 0,113 6 | 0,106 1 | 0,100 2 | 0,095 4 |
| 31 | 0,286 0 | 0,192 9 | 0,155 0 | 0,133 9 | 0,120 2 | 0,110 5 | 0,103 1 | 0,097 4 | 0,092 7 |
| 32 | 0,279 5 | 0,188 1 | 0,151 1 | 0,130 4 | 0,117 0 | 0,107 5 | 0,100 3 | 0,094 7 | 0,090 2 |
| 33 | 0,273 3 | 0,183 6 | 0,147 3 | 0,127 1 | 0,114 0 | 0,104 7 | 0,097 7 | 0,092 2 | 0,087 8 |
| 34 | 0,267 3 | 0,179 3 | 0,143 7 | 0,124 0 | 0,111 1 | 0,102 0 | 0,095 2 | 0,089 8 | 0,085 5 |
| 35 | 0,261 7 | 0,175 2 | 0,140 4 | 0,121 0 | 0,108 4 | 0,099 5 | 0,092 8 | 0,087 6 | 0,083 3 |
| 36 | 0,256 3 | 0,171 3 | 0,137 1 | 0,118 1 | 0,105 8 | 0,097 1 | 0,090 6 | 0,085 4 | 0,081 3 |
| 37 | 0,251 1 | 0,167 6 | 0,134 1 | 0,115 5 | 0,103 4 | 0,094 9 | 0,088 4 | 0,083 4 | 0,079 4 |
| 38 | 0,246 2 | 0,164 0 | 0,131 2 | 0,112 9 | 0,101 1 | 0,092 7 | 0,086 4 | 0,081 5 | 0,077 5 |
| 39 | 0,241 4 | 0,160 7 | 0,128 4 | 0,110 4 | 0,098 8 | 0,090 6 | 0,084 5 | 0,079 6 | 0,075 8 |
| 40 | 0,236 9 | 0,157 4 | 0,125 7 | 0,108 1 | 0,096 7 | 0,088 7 | 0,082 6 | 0,077 9 | 0,074 1 |
| CHÚ THÍCH 1: n là số kết quả lặp lại cho mỗi phương sai và p là số phương sai. CHÚ THÍCH 2: Chữ số thập phân cuối cùng của từng mục trong bảng đã được làm tròn lên để đảm bảo mức ý nghĩa. CHÚ THÍCH 3: Mỗi số trong bảng được lập dựa trên 50 triệu mô phỏng. | |||||||||
Bảng E.2 - Giá trị tới hạn 1 % của thống kê kiểm nghiệm Cochran
| p | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | n = 10 |
| 2 | 0,999 94 | 0,995 1 | 0,979 4 | 0,958 6 | 0,937 3 | 0,917 2 | 0,898 9 | 0,882 3 | 0,867 4 |
| 3 | 0,993 4 | 0,942 3 | 0,883 2 | 0,833 5 | 0,793 4 | 0,760 7 | 0,733 6 | 0,710 8 | 0,691 2 |
| 4 | 0,967 6 | 0,864 3 | 0,781 5 | 0,721 3 | 0,676 2 | 0,641 1 | 0,612 9 | 0,589 8 | 0,570 3 |
| 5 | 0,927 9 | 0,788 6 | 0,695 8 | 0,632 9 | 0,587 6 | 0,553 1 | 0,525 9 | 0,503 8 | 0,485 4 |
| 6 | 0,882 9 | 0,721 8 | 0,625 9 | 0,563 5 | 0,519 6 | 0,486 6 | 0,460 9 | 0,440 1 | 0,423 0 |
| 7 | 0,837 7 | 0,664 5 | 0,568 5 | 0,508 0 | 0,466 0 | 0,434 8 | 0,410 6 | 0,391 2 | 0,375 2 |
| 8 | 0,794 5 | 0,615 2 | 0,521 0 | 0,462 7 | 0,422 7 | 0,393 2 | 0,370 5 | 0,352 3 | 0,337 4 |
| 9 | 0,754 4 | 0,572 8 | 0,481 0 | 0,425 1 | 0,387 1 | 0,359 2 | 0,337 8 | 0,320 8 | 0,306 8 |
| 10 | 0,717 5 | 0,535 9 | 0,446 9 | 0,393 4 | 0,357 2 | 0,330 9 | 0,310 6 | 0,294 6 | 0,281 4 |
| 11 | 0,683 7 | 0,503 6 | 0,417 6 | 0,366 3 | 0,331 8 | 0,306 8 | 0,287 7 | 0,272 5 | 0,260 1 |
| 12 | 0,652 8 | 0,475 2 | 0,392 0 | 0,342 9 | 0,310 0 | 0,286 2 | 0,268 0 | 0,253 6 | 0,241 9 |
| 13 | 0,624 5 | 0,449 9 | 0,369 5 | 0,322 4 | 0,290 9 | 0,268 2 | 0,251 0 | 0,237 3 | 0,226 2 |
| 14 | 0,598 6 | 0,427 3 | 0,349 6 | 0,304 3 | 0,274 2 | 0,252 5 | 0,236 0 | 0,223 0 | 0,212 5 |
| 15 | 0,574 7 | 0,406 9 | 0,331 8 | 0,288 2 | 0,259 4 | 0,238 6 | 0,222 9 | 0,210 4 | 0,200 4 |
| 16 | 0,552 8 | 0,388 6 | 0,315 8 | 0,273 9 | 0,246 1 | 0,226 2 | 0,211 1 | 0,199 3 | 0,189 6 |
| 17 | 0,532 5 | 0,371 9 | 0,301 4 | 0,260 9 | 0,234 2 | 0,215 1 | 0,200 6 | 0,189 3 | 0,180 0 |
| 18 | 0,513 7 | 0,356 6 | 0,288 3 | 0,249 2 | 0,223 5 | 0,205 1 | 0,191 2 | 0,180 2 | 0,171 4 |
| 19 | 0,496 2 | 0,342 6 | 0,276 4 | 0,238 6 | 0,213 7 | 0,196 0 | 0,182 6 | 0,172 1 | 0,163 5 |
| 20 | 0,479 9 | 0,329 8 | 0,265 5 | 0,228 8 | 0,204 8 | 0,187 7 | 0,174 8 | 0,164 7 | 0,156 4 |
| 21 | 0,464 8 | 0,317 9 | 0,255 4 | 0,219 9 | 0,196 7 | 0,180 1 | 0,167 7 | 0,157 9 | 0,149 9 |
| 22 | 0,450 6 | 0,306 9 | 0,246 1 | 0,211 7 | 0,189 2 | 0,173 2 | 0,161 1 | 0,151 7 | 0,144 0 |
| 23 | 0,437 3 | 0,296 7 | 0,237 5 | 0,204 1 | 0,182 3 | 0,166 8 | 0,155 1 | 0,145 9 | 0,138 5 |
| 24 | 0,424 8 | 0,287 1 | 0,229 5 | 0,197 0 | 0,175 9 | 0,160 8 | 0,149 5 | 0,140 6 | 0,133 4 |
| 25 | 0,413 0 | 0,278 2 | 0,222 1 | 0,190 5 | 0,169 9 | 0,155 3 | 0,144 3 | 0,135 7 | 0,128 8 |
| 26 | 0,401 9 | 0,269 9 | 0,215 1 | 0,184 4 | 0,164 4 | 0,150 2 | 0,139 5 | 0,131 1 | 0,124 4 |
| 27 | 0,391 5 | 0,262 1 | 0,208 6 | 0,178 7 | 0,159 2 | 0,145 4 | 0,135 0 | 0,126 9 | 0,120 3 |
| 28 | 0,381 6 | 0,254 8 | 0,202 5 | 0,173 3 | 0,154 3 | 0,140 9 | 0,130 8 | 0,122 9 | 0,116 5 |
| 29 | 0,372 2 | 0,247 8 | 0,196 8 | 0,168 3 | 0,149 8 | 0,136 7 | 0,126 9 | 0,119 2 | 0,113 0 |
| 30 | 0,363 3 | 0,241 3 | 0,191 4 | 0,163 6 | 0,145 5 | 0,132 8 | 0,123 2 | 0,115 7 | 0,109 6 |
| 31 | 0,354 8 | 0,235 1 | 0,186 3 | 0,159 1 | 0,141 5 | 0,129 0 | 0,119 7 | 0,112 4 | 0,106 5 |
| 32 | 0,346 8 | 0,229 3 | 0,181 5 | 0,154 9 | 0,137 7 | 0,125 5 | 0,116 4 | 0,109 3 | 0,103 5 |
| 33 | 0,339 1 | 0,223 7 | 0,176 9 | 0,150 9 | 0,134 1 | 0,122 2 | 0,113 3 | 0,106 4 | 0,100 8 |
| 34 | 0,331 8 | 0,218 4 | 0,172 6 | 0,147 2 | 0,130 7 | 0,119 1 | 0,110 4 | 0,103 6 | 0,098 1 |
| 35 | 0,324 8 | 0,213 4 | 0,168 5 | 0,143 6 | 0,127 5 | 0,116 1 | 0,107 6 | 0,101 0 | 0,095 6 |
| 36 | 0,318 1 | 0,208 6 | 0,164 6 | 0,140 2 | 0,124 4 | 0,113 3 | 0,105 0 | 0,098 5 | 0,093 3 |
| 37 | 0,311 7 | 0,204 1 | 0,160 9 | 0,136 9 | 0,121 5 | 0,110 6 | 0,102 5 | 0,096 1 | 0,091 0 |
| 38 | 0,305 6 | 0,199 7 | 0,157 3 | 0,133 9 | 0,118 7 | 0,108 1 | 0,100 1 | 0,093 9 | 0,088 9 |
| 39 | 0,299 7 | 0,195 6 | 0,153 9 | 0,130 9 | 0,116 1 | 0,105 7 | 0,097 8 | 0,091 7 | 0,086 8 |
| 40 | 0,294 1 | 0,191 6 | 0,150 7 | 0,128 1 | 0,113 6 | 0,103 3 | 0,095 7 | 0,089 7 | 0,084 9 |
| CHÚ THÍCH 1: n là số kết quả lặp lại cho mỗi phương sai và p là số phương sai. CHÚ THÍCH 2: Chữ số thập phân cuối cùng của từng mục trong bảng đã được làm tròn lên để đảm bảo mức ý nghĩa. CHÚ THÍCH 3: Mỗi số trong bảng được lập dựa trên 50 triệu mô phỏng | |||||||||
Bảng E.3 - Giá trị tới hạn 0,1 % của thống kê kiểm nghiệm Cochran
| p | n = 2 | n = 3 | n = 4 | n = 5 | n = 6 | n = 7 | n = 8 | n = 9 | n = 10 |
| 2 | 0,999 999 4 | 0,999 6 | 0,995 6 | 0,987 1 | 0,975 5 | 0,962 5 | 0,949 2 | 0,936 1 | 0,923 6 |
| 3 | 0,999 4 | 0,981 8 | 0,946 3 | 0,907 9 | 0,872 6 | 0,841 4 | 0,814 2 | 0,790 3 | 0,769 3 |
| 4 | 0,993 0 | 0,937 1 | 0,870 3 | 0,813 2 | 0,766 8 | 0,728 8 | 0,697 3 | 0,670 8 | 0,648 1 |
| 5 | 0,997 0 | 0,881 1 | 0,794 6 | 0,728 8 | 0,678 4 | 0,638 8 | 0,606 8 | 0,580 3 | 0,558 0 |
| 6 | 0,952 9 | 0,824 5 | 0,727 1 | 0,657 9 | 0,606 8 | 0,567 6 | 0,536 4 | 0,510 9 | 0,489 7 |
| 7 | 0,923 8 | 0,771 4 | 0,668 5 | 0,598 7 | 0,548 5 | 0,510 5 | 0,480 6 | 0,456 4 | 0,436 3 |
| 8 | 0,892 3 | 0,723 1 | 0,618 0 | 0,549 1 | 0,500 3 | 0,463 9 | 0,435 4 | 0,412 5 | 0,393 6 |
| 9 | 0,860 2 | 0,679 6 | 0,574 4 | 0,507 0 | 0,460 0 | 0,425 9 | 0,398 1 | 0,376 5 | 0,358 7 |
| 10 | 0,828 5 | 0,640 7 | 0,536 4 | 0,471 0 | 0,425 8 | 0,392 5 | 0,366 9 | 0,346 4 | 0,329 6 |
| 11 | 0,798 0 | 0,605 7 | 0,503 2 | 0,439 8 | 0,396 4 | 0,364 7 | 0,340 3 | 0,320 9 | 0,305 0 |
| 12 | 0,768 8 | 0,574 3 | 0,473 9 | 0,412 6 | 0,371 0 | 0,340 6 | 0,317 4 | 0,298 9 | 0,283 9 |
| 13 | 0,741 2 | 0,545 9 | 0,447 8 | 0,388 6 | 0,348 7 | 0,319 6 | 0,297 4 | 0,279 9 | 0,265 6 |
| 14 | 0,715 2 | 0,520 2 | 0,424 6 | 0,367 4 | 0,329 0 | 0,301 1 | 0,279 9 | 0,263 2 | 0,249 5 |
| 15 | 0,690 6 | 0,496 9 | 0,403 7 | 0,348 4 | 0,311 4 | 0,284 7 | 0,264 5 | 0,248 4 | 0,235 4 |
| 16 | 0,667 6 | 0,475 6 | 0,384 8 | 0,331 4 | 0,295 7 | 0,270 1 | 0,250 6 | 0,235 3 | 0,222 8 |
| 17 | 0,645 9 | 0,456 1 | 0,367 7 | 0,315 9 | 0,281 6 | 0,256 9 | 0,238 2 | 0,223 5 | 0,211 6 |
| 18 | 0,625 5 | 0,438 1 | 0,352 1 | 0,302 0 | 0,268 8 | 0,245 0 | 0,227 0 | 0,212 9 | 0,201 4 |
| 19 | 0,606 3 | 0,421 6 | 0,337 8 | 0,289 2 | 0,257 2 | 0,234 2 | 0,216 9 | 0,203 3 | 0,192 2 |
| 20 | 0,588 2 | 0,406 3 | 0,324 6 | 0,277 5 | 0,246 5 | 0,224 4 | 0,207 6 | 0,194 5 | 0,183 9 |
| 21 | 0,577 1 | 0,392 1 | 0,312 5 | 0,266 8 | 0,236 7 | 0,215 3 | 0,199 2 | 0,186 5 | 0,176 2 |
| 22 | 0,555 0 | 0,378 9 | 0,301 3 | 0,256 9 | 0,227 7 | 0,207 0 | 0,191 4 | 0,179 1 | 0,169 2 |
| 23 | 0,539 8 | 0,366 6 | 0,290 9 | 0,247 7 | 0,219 4 | 0,199 3 | 0,184 2 | 0,172 3 | 0,162 8 |
| 24 | 0,525 4 | 0,355 1 | 0,281 2 | 0,239 2 | 0,211 7 | 0,192 2 | 0,177 6 | 0,166 1 | 0,156 8 |
| 25 | 0,511 8 | 0,344 3 | 0,272 1 | 0,231 2 | 0,204 6 | 0,185 6 | 0,171 4 | 0,160 3 | 0,151 3 |
| 26 | 0,498 8 | 0,334 2 | 0,263 7 | 0,223 8 | 0,197 9 | 0,179 5 | 0,165 7 | 0,154 8 | 0,146 1 |
| 27 | 0,486 5 | 0,324 6 | 0,255 8 | 0,216 9 | 0,191 6 | 0,173 7 | 0,160 3 | 0,149 8 | 0,141 3 |
| 28 | 0,474 9 | 0,315 7 | 0,248 3 | 0,210 4 | 0,185 8 | 0,168 4 | 0,155 3 | 0,145 1 | 0,136 9 |
| 29 | 0,463 8 | 0,307 2 | 0,241 3 | 0,204 3 | 0,180 3 | 0,163 3 | 0,150 6 | 0,140 7 | 0,132 7 |
| 30 | 0,453 2 | 0,299 2 | 0,234 7 | 0,198 6 | 0,175 2 | 0,158 6 | 0,146 2 | 0,136 5 | 0,128 7 |
| 31 | 0,443 1 | 0,291 6 | 0,228 5 | 0,193 2 | 0,170 3 | 0,154 1 | 0,142 1 | 0,132 6 | 0,125 0 |
| 32 | 0,443 4 | 0,284 4 | 0,222 6 | 0,188 0 | 0,165 7 | 0,149 9 | 0,138 1 | 0,128 9 | 0,121 5 |
| 33 | 0,424 2 | 0,277 6 | 0,217 0 | 0,183 2 | 0,161 4 | 0,146 0 | 0,134 4 | 0,125 5 | 0,118 2 |
| 34 | 0,415 4 | 0,271 1 | 0,211 7 | 0,178 6 | 0,157 3 | 0,142 2 | 0,131 0 | 0,122 2 | 0,115 1 |
| 35 | 0,406 9 | 0,264 9 | 0,206 7 | 0,174 3 | 0,153 4 | 0,138 6 | 0,127 6 | 0,119 1 | 0,112 2 |
| 36 | 0,398 8 | 0,259 0 | 0,201 9 | 0,170 1 | 0,149 7 | 0,135 3 | 0,124 5 | 0,116 1 | 0,109 4 |
| 37 | 0,391 0 | 0,253 4 | 0,197 3 | 0,166 2 | 0,146 1 | 0,132 0 | 0,121 5 | 0,113 3 | 0,106 7 |
| 38 | 0,383 6 | 0,248 0 | 0,192 9 | 0,162 4 | 0,142 8 | 0,129 0 | 0,118 7 | 0,110 6 | 0,104 2 |
| 39 | 0,376 4 | 0,242 9 | 0,188 8 | 0,158 8 | 0,139 6 | 0,126 1 | 0,116 0 | 0,108 1 | 0,101 8 |
| 40 | 0,369 5 | 0,238 0 | 0,184 8 | 0,155 4 | 0,136 5 | 0,123 3 | 0,113 4 | 0,105 7 | 0,099 5 |
| CHÚ THÍCH 1: n là số kết quả lặp lại cho mỗi phương sai và p là số phương sai. CHÚ THÍCH 2: Chữ số thập phân cuối cùng của từng mục trong bảng đã được làm tròn lên để đảm bảo mức ý nghĩa. CHÚ THÍCH 3: Mỗi số trong bảng được lập dựa trên 50 triệu mô phỏng | |||||||||
Phụ lục F
(tham khảo)
Hướng dẫn có cấu trúc phát hiện giá trị bất thường trong dữ liệu đơn biến
Cho một lô/mẫu về các quan trắc tập hợp các trung bình mẫu hoặc phương sai mẫu. Mục đích là phát hiện và nhận biết các giá trị bất thường có thể có trong tập dữ liệu. Phụ lục này hướng dẫn cho người sử dụng tiêu chuẩn này. Nó hướng dẫn người sử dụng thông qua một số bước bằng cách sử dụng các điều khác nhau trong tiêu chuẩn này. Việc ký hiệu tuân thủ theo tiêu chuẩn này.
Bước 1. Vẽ đồ thị tập dữ liệu cho x1, x2,…, xn sử dụng đồ thị phân tán, đồ thị phân thân và lá hoặc đồ thị hộp tiêu chuẩn hoặc xếp chúng theo thứ tự số tăng dần.
x(1) £ x(2) £ … £ x(k) £ … £ x(n)
trong đó x(i) là quan trắc nhỏ nhất thứ i.
Bước 2. Kiểm tra đồ thị và dữ liệu được sắp xếp của tập dữ liệu xem có các quan trắc bất thường hay không (giá trị bất thường nghi ngờ). Nếu các quan trắc bất thường không bị nghi ngờ là giá trị bất thường thì chuyển sang bước 5. Nếu một hoặc nhiều quan trắc bất thường có nghi ngờ tách biệt với phần chính của tập dữ liệu thì chuyển sang bước 3, ngược lại thì công bố là không có giá trị bất thường và sử dụng tập dữ liệu đã cho trong phân tích dữ liệu tiếp theo.
Bước 3. Xác nhận hoặc chuyển đổi phân bố của tập dữ liệu đã cho:
a) nếu phân bố giả thuyết là phân bố chuẩn thì xác nhận bằng đồ thị xác suất chuẩn;
b) nếu phân bố giả thuyết là phân bố hàm mũ thì xác nhận bằng đồ thị xác suất hàm mũ;
c) nếu phân bố giả thuyết là phân bố chuẩn lôga thì chuyển đổi tập dữ liệu đã cho thành dữ liệu chuẩn tương tự bằng cách sử dụng qui trình nêu trong 4.3.4.2, sau đó xác nhận bằng đồ thị xác suất chuẩn;
d) nếu phân bố giả thuyết là phân bố cực trị thì chuyển đổi tập dữ liệu đã cho thành dữ liệu hàm mũ tương tự bằng cách sử dụng qui trình nêu trong 4.3.4.3, sau đó xác nhận bằng đồ thị xác suất hàm mũ;
e) nếu phân bố giả thuyết là phân bố Weibull thì chuyển đổi tập dữ liệu đã cho thành dữ liệu hàm mũ tương tự bằng cách sử dụng qui trình nêu trong 4.3.4.4, sau đó xác nhận bằng đồ thị xác suất hàm mũ;
f) nếu phân bố giả thuyết là phân bố gamma thì chuyển đổi tập dữ liệu đã cho thành dữ liệu chuẩn tương tự bằng cách sử dụng qui trình nêu trong 4.3.4.5, sau đó xác nhận bằng đồ thị xác suất chuẩn;
g) nếu phân bố của tập dữ liệu đã cho là chưa biết hoặc phân bố giả định không thể xác nhận được hoặc không phải là một trong các phân bố nêu trên thì chuyển đổi tập dữ liệu thành dữ liệu chuẩn tương tự bằng cách sử dụng phép chuyển đổi Box-Cox hoặc Johnson, sau đó xác nhận bằng đồ thị xác suất chuẩn. Nếu không thể xác nhận tính chuẩn của dữ liệu chuyển đổi thì chuyển sang bước 6 và tiến hành phân tích dữ liệu sử dụng các quy trình ổn định nêu trong Điều 5.
Bước 4. Tiến hành (các) quy trình kiểm nghiệm để xác định xem các quan trắc bất thường xác định ở bước 2 có phải là giá trị bất thường hay không:
a) nếu tập dữ liệu ban đầu hoặc tập dữ liệu chuyển đổi giống với dữ liệu chuẩn thì sử dụng quy trình kiểm nghiệm ở 4.3.2 và/hoặc 4.4;
b) nếu tập dữ liệu ban đầu hoặc tập dữ liệu chuyển đổi giống với dữ liệu hàm mũ thì sử dụng quy trình kiểm nghiệm ở 4.3.3 và/hoặc 4.4.
Nếu một hoặc nhiều quan trắc bất thường được công bố là giá trị bất thường thì chuyển sang bước 5, nếu không thì công bố là không có giá trị bất thường và sử dụng tập dữ liệu ban đầu hoặc tập dữ liệu chuyển đổi cho phân tích dữ liệu tiếp theo.
Bước 5. Xác định nguyên nhân của giá trị bất thường được công bố.
Bước 6. Nếu có thể xác định được nguyên nhân của giá trị bất thường thì loại bỏ các giá trị bất thường và sử dụng các dữ liệu còn lại cho phân tích dữ liệu tiếp theo, nếu không thì sử dụng các quy trình ổn định cho phân tích dữ liệu tiếp theo.
Lưu đồ trên Hình F.1 tổng hợp các bước khuyến nghị trong việc phát hiện và xử lý giá trị bất thường
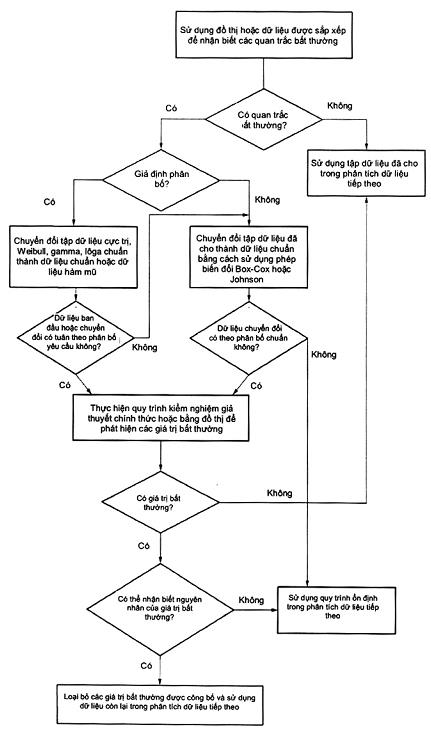
Hình F.1 - Lưu đồ phát hiện và xử lý các giá trị bất thường
THƯ MỤC TÀI LIỆU THAM KHẢO
[1] BARNETT, V. and LEWIS, T. Outliers in Statistical data. 3rd edition. New York: Wiley, 1994 (Giá trị bất thường trong dữ liệu thống kê)
[2] TUKEY, J.W. Exploratory data analysis. Reading, Massachusetts: Addison-Wesley, 1977 (Phân tích dữ liệu khảo sát)
[3] TCVN 6910-2:2001 (ISO 5725-2:1994), Độ chính xác (độ đúng và độ chụm) của phương pháp đo và kết quả đo. Phần 2: Phương pháp cơ bản xác định độ lặp lại và độ tái lặp của phương pháp đo tiêu chuẩn.
[4] ROSNER, B. Percentage Points for a Generalized ESD Many-Outlier Procedure. Technometrics, 25, 1983, pp. 165-172 (Điểm phần trăm đối với quy trình nhiều giá trị bất thường ESD tổng quát hóa)
[5] KIMBER, A.C., Tests for many outliers in an exponential sample. Applied Statistics, 31, 1982, pp. 263-271 (Kiểm nghiệm nhiều giá trị bất thường trong mẫu hàm mũ)
[6] KITTLITZ, R.G. Transforming the exponential for SPC applications. Journal of quality Technology, 31, 1999, pp. 301-308 (Chuyển đổi hàm mũ cho các ứng dụng SPC)
[7] BOX, G.E.P. and COX, D.R. An analysis of transformations. Journal of the Royal Statistical Society, Series B 26, 1964, pp. 211-246 (Phân tích các phép chuyển đổi)
[8] CHOU, Y., POLANSKY, A.M. and MASON, R.L. Transforming Nonnormal Data to Normality in Statistical Process Control. Journal of Quality Technology, 30, 1998, pp. 133-141 (Chuyển đổi dữ liệu không chuẩn thành chuẩn trong kiểm soát quá trình thống kê)
[9] HOAGLIN, D.C., MOSTELLER, F. and TUKEY, J.W. Understading robust and exploratory data analysis. New York: Wiley, 1983 (Hiểu biết về phân tích dữ liệu ổn định và dữ liệu khảo sát)
[10] ROUSSEEUW, P.J. and CROUX, C.Alternatives to the median absolute deviation. Journal of the American Statistical Association, 88, 1993, pp. 1273-1283 (Thay thế cho độ lệch tuyệt đối của trung vị)
[11] VERBOVEN, S. and HUBERT, M. LIBRA: a MATLAB Library for Robust Analysis, Chemometrics and Intelligent Laboratory Systems, 75, 2005, pp. 127-136 (Thư viện MATLAB dùng cho phân tích ổn định, Đo lường hóa học và hệ thống phòng thí nghiệm thông minh)
[12] KUTNER, M.H., NACHTSHEIM, C.J., NETER, J. and LI, W. Applied linear statistical models. Singapore: McGraw-Hill, 2005 (Mô hình thống kê tuyến tính ứng dụng)
[13] HUBER, P.J. Robust Statistics. New York: Wiley, 1981 (Thống kê ổn định)
[14] COOK, R.D. and WEISBERG, S. Residuals and influence in regression. London: Chapman & Hall, 1982 (Số dư và ảnh hưởng trong hồi quy)
[15] ROUSSEEUW, P.J. and LEROY, A.M. Robust Regression and Outlier Detection. New York: John Wiley, 1987 (Hồi quy ổn định và phát hiện giá trị bất thường)
[16] SIM, C.H., GAN, F.F. and CHANG, T.C. Outlier Labeling with Boxplot Procedures. Journal of the American Statistical Association, 100, 2005, pp. 642-652 (Ghi giá trị bất thường với quy trình đồ thị hộp)
[17] TCVN 8244-1:2010 (ISO 3534-1:2006), Thống kê học - Từ vựng và ký hiệu - Phần 1: Thuật ngữ chung về thống kê và thuật ngữ dùng trong xác suất
[18] TCVN 9603 (ISO 5479), Giải thích các dữ liệu thống kê - Kiểm nghiệm sai lệch so với phân bố chuẩn.
MỤC LỤC
Lời nói đầu
Lời giới thiệu
1. Phạm vi áp dụng
2. Thuật ngữ và định nghĩa
3. Ký hiệu
4. Giá trị bất thường trong dữ liệu đơn biến
4.1. Khái quát
4.2. Sàng lọc dữ liệu
4.3. Kiểm nghiệm các giá trị bất thường
5. Thỏa hiệp giá trị bất thường trong dữ liệu đơn biến
5.1. Phân tích dữ liệu ổn định
5.2. Ước lượng ổn định vị trí
5.3. Ước lượng ổn định của độ phân tán
6. Giá trị bất thường trong dữ liệu đa biến và hồi quy
6.1. Khái quát
6.2. Giá trị bất thường trong dữ liệu đa biến
6.3. Giá trị bất thường trong hồi quy tuyến tính
Phụ lục A (tham khảo) Thuật toán dùng cho quy trình phát hiện giá trị bất thường GESD
Phụ lục B (qui định) Giá trị tới hạn của thống kê kiểm nghiệm giá trị bất thường đối với mẫu hàm mũ
Phụ lục C (qui định) Giá trị hệ số của đồ thị hộp sửa đổi
Phụ lục D (qui định) Giá trị hệ số hiệu chỉnh đối với ước lượng ổn định của tham số thang đo
Phụ lục E (qui định) Giá trị tới hạn của thống kê kiểm nghiệm Cochran
Phụ lục F (tham khảo) Hướng dẫn có cấu trúc phát hiện giá trị bất thường trong dữ liệu đơn biến
Thư mục tài liệu tham khảo
1) Quy ước 2(1)40 đề cập đến các số từ 2 đến 40 với số gia 1.
Bạn chưa Đăng nhập thành viên.
Đây là tiện ích dành cho tài khoản thành viên. Vui lòng Đăng nhập để xem chi tiết. Nếu chưa có tài khoản, vui lòng Đăng ký tại đây!
 Tiêu chuẩn Việt Nam TCVN 8006-4:2013 PDF (Bản có dấu đỏ)
Tiêu chuẩn Việt Nam TCVN 8006-4:2013 PDF (Bản có dấu đỏ) Tiêu chuẩn Việt Nam TCVN 8006-4:2013 DOC (Bản Word)
Tiêu chuẩn Việt Nam TCVN 8006-4:2013 DOC (Bản Word)